數組(Array)是一種線性表資料結構。它用一組連續的記憶體空間來存儲一組具有相同資料類型的資料。
上述定義當中有有幾個較為關鍵的概念:
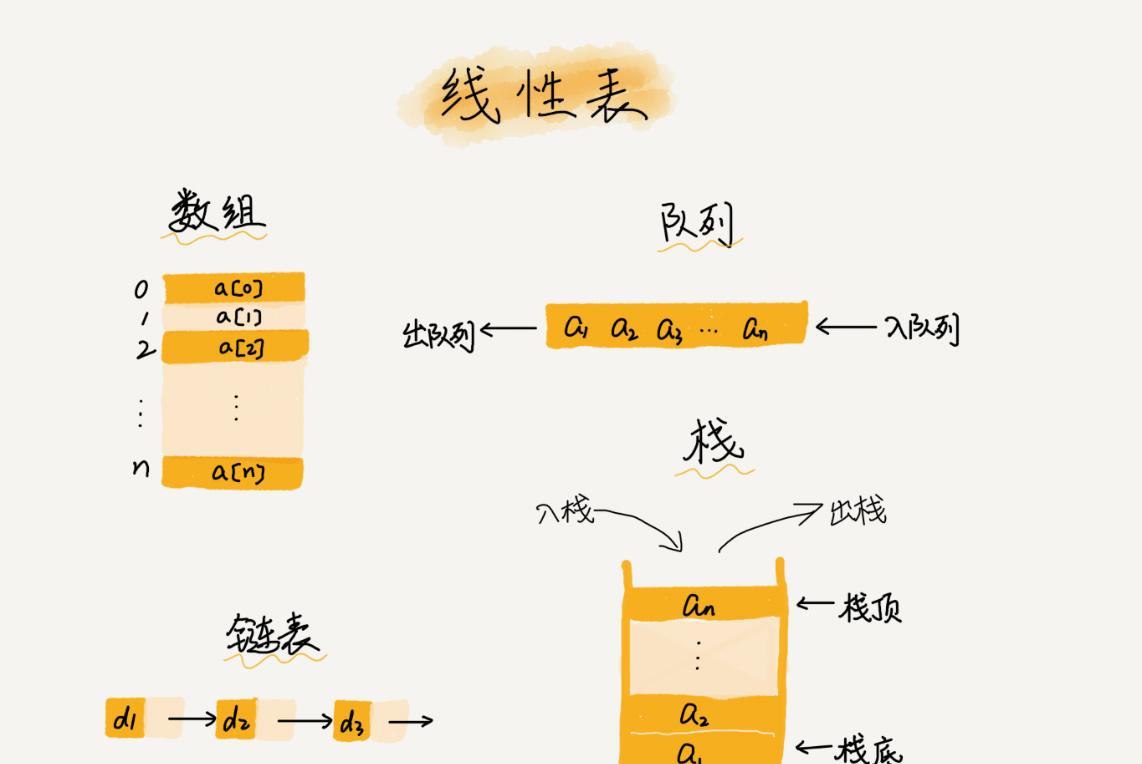
線性表 (Linear List)
線性表是指資料排成一個線型的結構。每個線性表上的資料最多隻有前後兩個方向。
除了數組之外,連結清單、隊列、棧也是線性表結構。
連續的記憶體空間和相同的資料類型
數組的随機通路(根據索引下标通路)時間複雜度為 O(1) 。其随機通路的實作原理是:
a[i]_address = base_address + i * data_type_size
為什麼大部分程式設計語言的數組下标是從 0 開始設計,而不是從 1 開始?
我們來思考另外一個問題,為什麼大部分程式設計語言的數組索引下标是從 0 開始,而不是從 1 開始?如果從 1 開始的話,上述的公式必須轉化為:
a[i]_address = base_address + ((i - 1) * data_type_size)
對比從 0 開始的方案,需要多做一次減法運算。是以大部分程式設計語言都選擇從 0 開始作為數組的初始下标。
低效的插入和删除操作
插入操作
假設數組的長度為 n ,我們需要将新元素 e 插入到數組中的第 k 個位置,那我們需要将後續的 n - k 個元素順序地往後進行移動,是以在這種場景下插入操作的時間複雜度為 O(n) 。
但是有一種特殊場景下:數組僅僅作為一種容器去存儲資料,而不用關心數組中存儲元素的順序,能夠将數組插入操作的算法複雜度提升為 O(1) 。
舉個例子,假設資料 a[10] 中存儲了 5 個元素: a、b、c、d、e 。我們将元素 x 插入到第三個位置,隻需要将原有的第三個元素 c 移動到最後,再将第三個元素替換為 x ,具體的實作代碼如下:
a[5] = c;
a[2] = x;
删除操作
與插入操作類似,如果我們要删除第 k 個位置的資料,為了記憶體的連續性,也需要搬移資料,是以數組的删除操作時間複雜度為 O(n) 。
有一種數組删除操作的優化方案是,不需要每一次删除操作時都移動資料,而是先将被删除的索引位置記錄下來,等到數組容量不足時,再一次性地從記憶體當中移除資料,并移動剩餘元素的位置。其核心思想與 JVM 的标記清除記憶體回收算法非常相似。
數組與容器類型的對比
許多程式設計語言中都提供了進階的容器類型,例如 Java 的 ArrayList , C++ 的 Vector 等,數組與這些進階容器類型相比,有哪些适合的應用場景了?
适合使用容器類型的場景
進階容器類型支援動态擴容,适合存儲元素的大小無法事先确定的場景。例如 ArrayList 會在存儲空間不足時,自動擴容 1.5 倍。需要注意的是,我們應該養成設定 ArrayList 初始容量的習慣,因為這樣能夠節省掉很多次記憶體配置設定空間和資料搬移的操作。
//假設從 db 當中擷取使用者的資料為 10000條
//指定初始容量為 10000 會比不指定容量獲得更好的性能
ArrayList<User> list = new ArrayList<User>(10000);
for (int i = 0; i < db.getUserList(); i++) {
list.add(db[i]);
}
适合使用數組的場景
ArrayList 無法存儲基本類型:int 、long 等,隻能存儲包裝類型: Integer 、Long ,而 Boxing 和 UnBoxing 會有一定的性能損耗,如果特别關注性能,就可以使用數組。
Java implemention
初步實作了類似于 ArrayList 的代碼。ref here
JDK 1.8 ArrayList 的實作代碼。ref here