XGBoost和Random-Forest(RF,随機森林)都屬于內建學習(Ensemble Learning),內建學習的目的是通過結合多個基學習器的預測結果來改善單個學習器的泛化能力和魯棒性,通過組合各個決策樹的輸出來進行預測(分類或回歸)。而內建學習按照個體學習器的生成方式,可以大緻分為兩類:一類是個體學習器之間存在強依賴關系,必須串行生成序列的方法;以及個體學習器之間不存在強依賴關系,可同時生成的并行化方法。前者的代表就是XGBoost,後者的代表是Random-Forest。
在這篇文章中,将嘗試解釋如何使用XGBoost和随機森林這兩種非常流行的貝葉斯優化方法,而不僅僅是比較這兩種模型的主要優點和缺點。
XGBoost vs Random Forest
XGBoost
XGBoost每次建構一個決策樹,每個新樹校正由先前訓練的決策樹産生的錯誤。
XGBoost應用示例
Addepto公司使用XGBoost模型來解決異常檢測問題,例如在監督學習方法中,XGB在這種情況下是非常有用的,因為異常檢測資料集通常是非常不平衡,比如手機APP中的使用者/消費者交易,能量消耗或使用者行為等,這些資料也經常用于推薦模型等訓練資料,XGBoost模型在推薦系統中也是經典模型之一。
優點
由于提升樹是通過優化目标函數得到的,是以XGB基本上可以用來解決幾乎所有可以求導的目标函數,包括排名和泊松回歸等内容,這是随機森林模型難以實作。
缺點
如果資料中存在噪聲,那麼XGB模型可能會對過拟合會更為敏感。由于樹模型是按順序建造的,是以訓練通常需要花費更長的時間。此外,XGB比随機森林更難調參,XGB通常有三個參數:樹的數量,樹的深度和學習率。一般而言,建構的每個樹通常是淺的。
随機森林
随機森林(RF)使用随機資料樣本獨立訓練每棵樹,這種随機性有助于使得模型比單個決策樹更健壯。由于這個原因,随機森林算法在訓練資料上不太可能出現過拟合現象。
随機森林應用示例
随機森林的差異性已被用于各種應用,例如基于組織标記資料找到患者群$[1]$。 在以下兩種情況下,随機森林模型對于這種應用非常實用:
- 目标是為具有強相關特征的高維問題提供高預測精度;
- 資料集非常嘈雜,并且包含許多缺失值,例如某些屬性是半連續的;
随機森林中的模型參數調整比XGBoost更容易。在随機森林中,隻有兩個主要參數:每個節點要選擇的特征數量和決策樹的數量。此外,随機森林比XGB更難出現過拟合現象。
随機森林算法的主要限制是大量的樹使得算法對實時預測的速度變得很慢。對于包含不同級别數的分類變量的資料,随機森林偏向于具有更多級别的屬性。
貝葉斯優化
貝葉斯優化是一種優化函數的技術,其評估成本很高$[2]$。它為目标函數建構後驗分布,并使用高斯過程回歸計算該分布中的不确定性,然後使用采集函數(acquisition function )來決定采樣的位置。貝葉斯優化專注于解決問題:
$max(_x∈AF(X))$
超參數的次元($x∈R_d$)一般設定為$d<20$。
通常設定A超矩形($x∈R^d$:$a_i≤x_i≤b_i$)。目标函數是連續的,這是使用高斯過程回歸模組化所需的。它也缺乏像凹函數或線性函數這類函數,這使得利用這類函數來提高效率的技術徒勞無功。貝葉斯優化由兩個主要組成部分組成:用于對目标函數模組化的貝葉斯統計模型和用于決定下一步采樣的采集函數。
在根據初始空間初始化實驗設計的評估目标後,疊代使用這些目标配置設定N個評估的預算的剩餘部分,如下所示:
- 觀察初始點;
- 當$n\leqN$ 時,使用所有可用資料更新後驗機率分布,并讓$x_n$作為采集函數的最大值時的取值。繼續觀察$y_n=f(x_n)$ ,增大$n$, 直到循環結束;
- 傳回一個解決方案:最大的評估點;
通過上述可以總結到,貝葉斯優化是為黑盒無導數全局優化而設計的,在機器學習中調整超參數中是非常受歡迎的。
下面是整個優化的圖形做總結:具有後驗分布的高斯過程以及觀察值和置信區間,以及效用函數(Utility Function),其中最大值表示下一個樣本點。
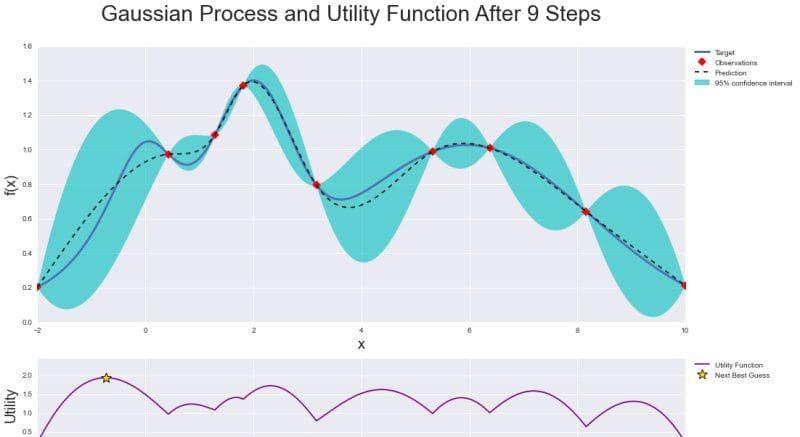
由于效用函數的存在,貝葉斯優化在機器學習算法的參數調整方面比網格(grid)或随機搜尋技術(random search)更有效,它可以有效地平衡“探索”和“開發”在尋找全局最優中的作用。
實踐
為了實作貝葉斯優化,使用Python編寫的
BayesianOptimization庫$[3]$來調整随機森林和XGBoost分類算法的超參數。首先需要通過pip安裝它:
pip install bayesian-optimization 現在開始訓練模型。首先導入所需要的依賴庫:
#Import libraries
import pandas as pd
import numpy as np
from bayes_opt import BayesianOptimization
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
import xgboost as xgb 下面定義了一個函數來運作給定資料的貝葉斯優化,以及要優化的函數及其超參數:
#Bayesian optimization
def bayesian_optimization(dataset, function, parameters):
X_train, y_train, X_test, y_test = dataset
n_iterations = 5
gp_params = {"alpha": 1e-4}
BO = BayesianOptimization(function, parameters)
BO.maximize(n_iter=n_iterations, **gp_params)
return BO.max 下面定義了優化函數,即随機森林分類器及其超參數$n\_estimators$,$max\_depth$和$min\_samples\_split$。另外,對給定資料集使用交叉驗證獲得分數的平均值:
def rfc_optimization(cv_splits):
def function(n_estimators, max_depth, min_samples_split):
return cross_val_score(
RandomForestClassifier(
n_estimators=int(max(n_estimators,0)),
max_depth=int(max(max_depth,1)),
min_samples_split=int(max(min_samples_split,2)),
n_jobs=-1,
random_state=42,
class_weight="balanced"),
X=X_train,
y=y_train,
cv=cv_splits,
scoring="roc_auc",
n_jobs=-1).mean()
parameters = {"n_estimators": (10, 1000),
"max_depth": (1, 150),
"min_samples_split": (2, 10)}
return function, parameters 類似地,為XGBoost分類器定義函數和超參數:
def xgb_optimization(cv_splits, eval_set):
def function(eta, gamma, max_depth):
return cross_val_score(
xgb.XGBClassifier(
objective="binary:logistic",
learning_rate=max(eta, 0),
gamma=max(gamma, 0),
max_depth=int(max_depth),
seed=42,
nthread=-1,
scale_pos_weight = len(y_train[y_train == 0])/
len(y_train[y_train == 1])),
X=X_train,
y=y_train,
cv=cv_splits,
scoring="roc_auc",
fit_params={
"early_stopping_rounds": 10,
"eval_metric": "auc",
"eval_set": eval_set},
n_jobs=-1).mean()
parameters = {"eta": (0.001, 0.4),
"gamma": (0, 20),
"max_depth": (1, 2000)}
return function, parameters
現在,基于選擇的分類器,可以對其進行優化并訓練模型:
#Train model
def train(X_train, y_train, X_test, y_test, function, parameters):
dataset = (X_train, y_train, X_test, y_test)
cv_splits = 4
best_solution = bayesian_optimization(dataset, function, parameters)
params = best_solution["params"]
model = RandomForestClassifier(
n_estimators=int(max(params["n_estimators"], 0)),
max_depth=int(max(params["max_depth"], 1)),
min_samples_split=int(max(params["min_samples_split"], 2)),
n_jobs=-1,
random_state=42,
class_weight="balanced")
model.fit(X_train, y_train)
return model 作為示例資料,使用來自AdventureWorksDW2017 SQL Server資料庫的視圖。在該資料庫中,根據個人資料,需要預測是否有人購買自行車。這裡隻給出貝葉斯優化在随機森林算法上的結果:
| ITER | AUC | max_depth | min_samples_split | n_estimators |
|---|---|---|---|---|
| 1 | 0.8549 | 45.88 | 6.099 | 34.82 |
| 2 | 0.8606 | 15.85 | 2.217 | 114.3 |
| 3 | 0.8612 | 47.42 | 8.694 | 306.0 |
| 4 | 0.8416 | 10.09 | 5.987 | 563.0 |
| 5 | 0.7188 | 4.538 | 7.332 | 766.7 |
| 6 | 0.8436 | 100.0 | 448.6 | |
| 7 | 0.6529 | 1.012 | 2.213 | 315.6 |
| 8 | 0.8621 | 10.0 | 1E + 03 | |
| 9 | 0.8431 | 154.1 | ||
| 0.653 | ||||
| 11 | 668.3 | |||
| 12 | 0.8437 | 867.3 | ||
| 13 | 0.637 | |||
| 14 | 0.8518 | |||
| 15 | 0.8435 | 317.6 | ||
| 16 | 559.7 | |||
| 17 | 89.86 | 82.96 | ||
| 18 | 0.8616 | 49.89 | 212.0 | |
| 19 | 0.8622 | 771.7 | ||
| 20 | 38.33 | 469.2 | ||
| 21 | 39.43 | 638.6 | ||
| 22 | 83.73 | 384.9 | ||
| 23 | 936.1 | |||
| 24 | 0.8428 | 54.2 | 2.259 | 122.4 |
| 25 | 0.8617 | 99.62 | 9.856 | 254.8 |
從上面的結果可以看到,貝葉斯優化在第23步疊代中找到了最佳參數,在測試資料集上得到0.8622 AUC分數。如果資料樣本更多,實驗結果可能會更好。優化的随機森林模型具有以下ROC-AUC曲線:
在機器學習研究$[4]$中,可以引入一種簡單的超參數調整方法——貝葉斯優化,貝葉斯優化比網格或随機搜尋政策能更快地找到最優值。
- https://www.researchgate.net/publication/225175169
- https://en.wikipedia.org/wiki/Bayesian_optimization
- https://github.com/fmfn/BayesianOptimization
- https://addepto.com/automated-machine-learning-tasks-can-be-improved/
作者資訊
文由阿裡雲開發者社群組織翻譯。
文章原标題《XGBoost and Random Forest with Bayesian Optimisation》
作者:Edwin Lisowski
譯者:海棠
文章為簡譯,更為詳細的内容,請檢視
原文