是以代碼附上GitHub: https://github.com/GreenArrow2017/DataStructure_Java/tree/master/out/production/DataStructure_Java/ApplicationOfAlgorithm
排序可視化
SelectionSort
選擇排序很簡單,所有的排序算法在前面的部落格都有講解:
https://www.jianshu.com/p/7fbf8671c742
選擇排序很簡單,周遊所有元素,檢視一下他們的之後最小的元素和目前元素交換即可。模闆函數使用上面的swing模闆。為了更清楚顯示出排序的過程,可以用不同顔色代表排好序和未排好序的。
int w = canvasWidth / data.N();
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.LightBlue);
for (int i = 0; i < data.N(); i++) {
if (i < data.orderIndex) {
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Red);
} else {
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Grey);
}
if (i == data.currentIndex) {
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Indigo);
}
if (i == data.currentComperent) {
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.LightBlue);
}
AlgorithmHelper.fillRectangle(graphics2D, i * w, canvasHeight - data.get(i), w - 1, data.get(i));
}
}
Frame的畫圖函數主要構成部分,其餘的都是模闆,為了抽象性,是以把selection的資料集中起來形成一個新的類,包括了生成資料等等。
public class SelectionSortData {
private int[] numbers;
public int orderIndex = -1;
public int currentIndex = -1;
public int currentComperent = -1;
public SelectionSortData(int N, int randomBound) {
numbers = new int[N];
for (int i = 0; i < N; i++) {
numbers[i] = (int) (Math.random() * randomBound) + 1;
//System.out.println(numbers[i]);
}
}
public void setData(int orderIndex, int currentComperent, int currentIndex){
this.currentIndex = currentIndex;
this.currentComperent = currentComperent;
this.orderIndex = orderIndex;
}
public int N(){
return numbers.length;
}
public int get(int index){
if (index < 0 || index >= numbers.length){
throw new IllegalArgumentException("index is illgel!");
}
return numbers[index];
}
public void swap(int i, int j){
int t = numbers[i];
numbers[i] = numbers[j];
numbers[j] = t;
}
}
在這個資料類裡面有三個屬性,分别是已經排好序的索引,目前最小值,目前正在比較的索引。在渲染過程中需要改變就是這幾個顔色了。是以動态的效果主要來源就是通過改變着幾個值即可。
private void run() {
data.setData(0,-1,-1);
frame.render(data);
AlgorithmHelper.pause(DELAY);
for (int i = 0; i < data.N(); i++) {
int midIndex = i;
data.setData(i, -1, midIndex);
frame.render(data);
AlgorithmHelper.pause(DELAY);
for (int j = i+1; j < data.N(); j++) {
data.setData(i, j, midIndex);
frame.render(data);
AlgorithmHelper.pause(DELAY);
if (data.get(j) < data.get(midIndex)){
midIndex = j;
data.setData(i, j, midIndex);
frame.render(data);
AlgorithmHelper.pause(DELAY);
}
}
data.swap(i, midIndex);
data.setData(i+1, -1, -1);
frame.render(data);
AlgorithmHelper.pause(DELAY);
}
data.setData(data.N(), -1,-1);
frame.render(data);
AlgorithmHelper.pause(DELAY);
}
檢視一下效果:
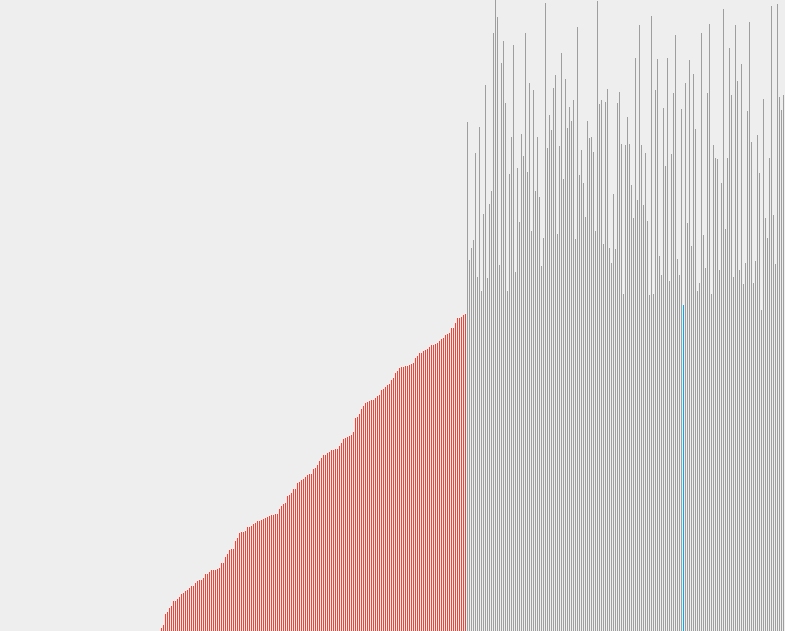
InsertionSort
插入排序也很簡單,沒有涉及到遞歸操作等等。每周遊一個元素,看看這個元素和之前比較過的位置是在那裡,像打牌的時候插排一樣。和之前的查找一樣,已經排好序的位置就直接用紅色表示,目前對比位置用藍色表示。首先是畫圖paintComponent:
int w = canvasWidth / data.N();
for (int i = 0; i < data.N(); i++) {
if (i < data.orderIndex){
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Red );
}else {
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Grey);
}
if (i == data.currentIndex){
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.LightBlue);
}
AlgorithmHelper.fillRectangle(graphics2D, i * w, canvasHeight - data.get(i), w - 1, data.get(i));
}
}
和上面的選擇排序差不多。
private void run() {
setData(-1, -1);
for (int i = 0; i < data.N(); i++) {
setData(i, i);
for (int j = i; j > 0 && data.get(j) < data.get(j - 1); j--) {
data.swap(j, j - 1);
setData(i+1, j-1);
}
setData(i, -1);
}
setData(data.N(), -1);
}
private void setData(int orderIndex, int currentIndex){
data.orderIndex = orderIndex;
data.currentIndex = currentIndex;
frame.render(data);
AlgorithmHelper.pause(DELAY);
}
都是正常操作。
MergeSort
歸并排序本身的思路,面對一個數組想要讓他排序,首先把數組分成兩部分,用同樣的算法把兩邊排序,最後歸并兩邊。在劃分的時候,劃分到不能再劃分為止。首先同樣要有一個歸并的資料類:
public class MergeData {
private int[] numbers;
public int l, r;
public int mergeIndex;
public MergeData(int N, int randomBound) {
numbers = new int[N];
for (int i = 0; i < N; i++) {
numbers[i] = (int) (Math.random() * randomBound) + 1;
//System.out.println(numbers[i]);
}
}
public int N(){
return numbers.length;
}
public int get(int index){
if (index < 0 || index >= numbers.length){
throw new IllegalArgumentException("index is illgel!");
}
return numbers[index];
}
public void set(int index, int num){
if (index < 0 || index >= numbers.length){
throw new IllegalArgumentException("index is illgel!");
}
numbers[index] = num;
}
public void swap(int i, int j){
int t = numbers[i];
numbers[i] = numbers[j];
numbers[j] = t;
}
}
用l和r來表示正在歸并的數組範圍,mergeIndex表示已經進行歸并了的集合。歸并整個過程前面的部落格有寫,不再複述了。
private void run() {
setData(-1, -1, -1 );
Merge(0, data.N()-1);
setData(0, data.N()-1, -1);
}
private void Merge(int l, int r) {
if (l >= r) {
return;
}
setData(l, r, -1);
int mid = (l + r) / 2;
Merge(l, mid);
Merge(mid + 1, r);
merge(l, r, mid);
}
private void merge(int l, int r, int mid) {
int[] array = new int[r - l + 1];
for (int i = l; i <= r; i++) {
array[i - l] = data.get(i);
}
int i = l, j = mid + 1;
int index = l;
while (i <= mid && j <= r) {
if (array[i - l] < array[j - l]) {
data.set(index, array[i - l]);
i++;
index++;
} else {
data.set(index, array[j - l]);
j++;
index++;
}
setData(l, r, index);
}
if (i <= mid) {
for (int k = i; k <= mid; k++) {
data.set(index, array[k - l]);
index++;
setData(l, r, index);
}
} else if (j <= r) {
for (int k = j; k <= r; k++) {
data.set(index, array[k - l]);
index++;
setData(l, r, index);
}
}
}
效果:
QuickSort
快速排序,快速排序是在平均情況下比較快的算法了。每一次把第一個元素作為标定的位置,把這個位置放到合适的位置即可。首先還是需要一個快拍資料類:
public class QuickSortData {
private int[] numbers;
public int l, r;
public int Index;
public QuickSortData(int N, int randomBound) {
numbers = new int[N];
for (int i = 0; i < N; i++) {
numbers[i] = (int) (Math.random() * randomBound) + 1;
//System.out.println(numbers[i]);
}
}
public int N(){
return numbers.length;
}
public int get(int index){
if (index < 0 || index >= numbers.length){
throw new IllegalArgumentException(index + "index is illgel!");
}
return numbers[index];
}
public void set(int index, int num){
if (index < 0 || index >= numbers.length){
throw new IllegalArgumentException("index is illgel!");
}
numbers[index] = num;
}
public void swap(int i, int j){
int t = numbers[i];
numbers[i] = numbers[j];
numbers[j] = t;
}
}
和前面的歸并排序一樣,l和r用不同的顔色。
private void run() {
setData(-1, -1, -1);
QuickSort(0, data.N() - 1);
setData(0, data.N() - 1, -1);
}
private void QuickSort(int l, int r) {
if (l >= r) {
return;
}
setData(l, r, -1);
int mid = partition(l, r);
QuickSort(l, mid - 1);
QuickSort(mid + 1, r);
frame.render(data);
AlgorithmHelper.pause(DELAY);
}
private int partition(int l, int r) {
int v = data.get(l);
int i = l + 1;
int j = r;
setData(l, r, l);
while (true) {
while (i <= r && data.get(i) < v) {
i++;
}
while (j >= l + 1 && data.get(j) > v) {
j--;
}
if (i > j) {
break;
}
data.swap(i, j);
setData(l, r, l);
i++;
j--;
}
data.swap(j, l);
setData(l, r, j);
return j;
}
和前面基本一緻。
走迷宮
顯示迷宮
迷宮生成等等再提,先看一下迷宮的讀取和顯示。
第一行是行數和列數,代表有101行101列,這個迷宮後面可以使用最小生成樹生成。讀進一個迷宮:
public class MazeData {
private char[][] maze;
private int N, M;
public static final char ROAD = '#';
public static final char WALL = ' ';
public MazeData(String fileName) {
if (fileName == null) {
throw new IllegalArgumentException("filename can't be null!");
}
Scanner scanner = null;
try {
File file = new File(fileName);
if (!file.exists()) {
throw new IllegalArgumentException("File is not exist!");
}
FileInputStream fileInputStream = new FileInputStream(file);
scanner = new Scanner(new BufferedInputStream(fileInputStream), "UTF-8");
String nm = scanner.nextLine();
String[] nmC = nm.trim().split("\\s+");
N = Integer.parseInt(nmC[0]);
M = Integer.parseInt(nmC[1]);
maze = new char[N][M];
for (int i = 0; i < N; i++) {
String line = scanner.nextLine();
if (line.length() != M) {
throw new IllegalArgumentException("Message of file is not completed!");
}
for (int j = 0; j < M; j++) {
maze[i][j] = line.charAt(j);
}
}
} catch (Exception e) {
e.printStackTrace();
} finally {
if (scanner != null) {
scanner.close();
}
}
}
public char getMaze(int i, int j) {
if (!inArea(i, j)) {
throw new IllegalArgumentException("out of range!");
}
return maze[i][j];
}
public boolean inArea(int x, int y) {
return x >= 0 && x < N && y >= 0 && y < M;
}
public int N() {
return N;
}
public int M() {
return M;
}
}
使用File來獲得目前檔案,如果沒有就要抛出異常。scanner獲得輸入流之後可以通過讀取下一行獲得每一行的内容,列數在前面已經提到了,是以要檢查每一行是不是M列,不是就沒得讀了。#就是牆,空格是路,可以設定兩個靜态變量表示。同時還需要各種輔助函數,比如是否是在整區域裡面的,傳回目前區域的值等等。然後就是顯示函數了:
int w = canvasWidth / data.M();
int h = canvasHeight / data.N();
for (int i = 0; i < data.N(); i++) {
for (int j = 0; j < data.M(); j++) {
if (data.getMaze(i, j) == MazeData.ROAD){
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.LightBlue);
}else {
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.White);
}
AlgorithmHelper.fillRectangle(graphics2D, j * w, i * h, w, h);
}
}
牆的寬度自适應,這樣整個螢幕剛剛夠。#号畫淺藍色,其餘的白色。之後就是再控制器裡面調用repaint即可。
迷宮問題
白色方塊是可以走的路徑,紅色的就是牆。迷宮的本質就是一個圖結構。可以把整個迷宮當成是一個圖,而走迷宮的過程就可以等價成是圖的周遊。從起始點開始周遊,直到周遊到了某一個終止點即可。如果周遊了所有點都沒有得到結果,那麼就可以确認無解了。
圖的周遊可以分成兩種周遊。深度優先周遊和廣度優先周遊,一種周遊是按照深度,先往一個方向深了走,沒有路了再回頭,而廣度是先廣度走一遍再一層一層下去。首先固定了每一個迷宮的出口和入口位置,從一開始,就需要從相鄰的四個方向走迷宮,如果可以就繼續,不能就回頭,其實就是遞歸實作。
深度優先
首先還是遞歸實作,遞歸比較友善,首先要準備遞歸函數,和上述的一樣,走四個方向,一個一個嘗試,如果下一個格子是在這個圖裡面,是一條路,而且還沒有被通路過,那麼久可以繼續走,否則就需要傳回。
private boolean go(int x, int y) {
if (!data.inArea(x, y)) {
throw new IllegalArgumentException("Paramenter is illgel!");
}
data.visited[x][y] = true;
setData(x, y, true);
if (x == data.getExitX() && y == data.getExitY()) {
return true;
} else {
for (int i = 0; i < 4; i++) {
int nexX = x + direction[i][0];
int nexY = y + direction[i][1];
if (data.inArea(nexX, nexY) &&
data.getMaze(nexX, nexY) == MazeData.ROAD &&
!data.visited[nexX][nexY]) {
if (go(nexX, nexY)) {
return true;
}
}
}
setData(x, y, false);
return false;
}
}
如果四個點都嘗試過了,都是走不了的,那麼還需要消除畫的格子。相對來說還是比較簡單的。再消除格子上這個步驟對于遞歸來說是相對友善,因為再回溯的過程中是有保留之前的點的資訊的,是以相對簡單。
這就是生成的結果了。
如果是非遞歸,用棧就可以模拟,因為遞歸本身就是用棧實作的。對于删除無用路徑的情況,其實有點難,因為無用的路徑是直接丢棄的,先前的遞歸可以是因為遞歸的棧保留了更加多的内容,而這裡隻是保留了點而已。
private boolean go_iteration() {
Stack<Position> stack = new Stack<>();
Position entrance = new Position(data.getEntanceX(), data.getEntanceY());
stack.push(entrance);
data.visited[entrance.getX()][entrance.getY()] = true;
while (!stack.isEmpty()) {
Position position = stack.pop();
setData(position.getX(), position.getY(), true);
for (int i = 0; i < 4; i++) {
int newX = position.getX() + direction[i][0];
int newY = position.getY() + direction[i][1];
if (newX == data.getExitX() && newY == data.getExitY()) {
setData(newX, newY, true);
return true;
}
Position newPosition = new Position(newX, newY, position);
if (data.inArea(newPosition.getX(), newPosition.getY()) &&
data.getMaze(newPosition.getX(), newPosition.getY()) == MazeData.ROAD
&& !data.visited[newPosition.getX()][newPosition.getY()]) {
stack.push(newPosition);
data.visited[newPosition.getX()][newPosition.getY()] = true;
}
}
}
return false;
}
廣度優先
廣度和深度在搜尋政策上是不同的。深度是走到死路才回頭,廣度是對于每一次都是齊頭并進。和周遊的深度優先的差別就是在于他們的資料結構不一樣,一個是隊列,一個是棧,其他的基本差不多。
private boolean go_level() {
Queue<Position> queue = new LinkedList<>();
Position position = new Position(data.getEntanceX(), data.getEntanceY());
queue.add(position);
data.visited[position.getX()][position.getY()] = true;
while (!queue.isEmpty()) {
Position position1 = queue.poll();
setData(position1.getX(), position1.getY(), true);
for (int i = 0; i < 4; i++) {
int newX = position1.getX() + direction[i][0];
int newY = position1.getY() + direction[i][1];
if (newX == data.getExitX() && newY == data.getExitY()) {
findPath(position1);
setData(newX, newY, true);
return true;
}
Position newPosition = new Position(newX, newY, position1);
if (data.inArea(newPosition.getX(), newPosition.getY()) &&
data.getMaze(newPosition.getX(), newPosition.getY()) == MazeData.ROAD
&& !data.visited[newPosition.getX()][newPosition.getY()]) {
queue.add(newPosition);
data.visited[newPosition.getX()][newPosition.getY()] = true;
}
}
}
return false;
}
如果迷宮有很多個解,深度優先周遊那麼久隻會搜尋到第一個碰到的解,搜尋到的解那麼就是一個随緣排序出來,廣度優先就是會查找最短的路徑。廣度優先可以找到無全圖的最短路徑。深度和廣度的非遞歸差不多,隻是使用的資料結構不同而已。
生成迷宮
剛剛是走迷宮,剛剛生成的那個用例其實就是生成的迷宮。對于一個迷宮,隻有一個入口一個出口,為了簡單化,入口就是第二行的第一個口,出口是倒數第二行的第一個口。而且隻有一個解,并且路徑是連續的,有些遊戲裡面的迷宮是有傳送點的,改變起來也很簡單。
首先迷宮其實就是一棵樹,每一個點都會有分支,任何一個葉子或者是節點都可以作為是一個入口,生成一個迷宮其實就是一個生成樹的過程。之前在資料結構有提到過一個最小生成樹,但是由于是一個随機的迷宮,是以應該是随機生成樹。無論是什麼樹,都是基于樹的。而圖的周遊結果就是一顆樹,每一個節點隻是通路一次,且沒有環,深度優先周遊的結果是一顆深度優先樹,廣度優先的結果是廣度優先樹。可以先把一張畫布分成很多很多小格子,然後每隔一個格子就挖空一個點,沒有挖空點的都是牆,用一種周遊方法來周遊這些點所生成的樹就是一個迷宮了。但是這樣的迷宮其實帶有偏見的,随機性不高,是以可以在選擇點的進行周遊的時候進行随機選擇。
@@@@@
@ _@ _ @
@ _ @ _@
可以看的出無論怎麼看,行和列一定要是基數,限制還是蠻多的。深度優先生成迷宮其實和之前的差不多,沒有上面打的差别。首先是要得到一個格子布。然後通過深度周遊把格子全部連接配接起來。遞歸實作:
private void run() {
setData(-1, -1);
go(data.getEntranceX(), data.getEntranceY() + 1);
setData(-1, -1);
}
private void go(int x, int y) {
if (!data.inArea(x, y)) {
throw new IllegalArgumentException("x or y is illegal!");
}
data.visited[x][y] = true;
for (int i = 0; i < 4; i++) {
int newX = x + direction[i][0] * 2;
int newY = y + direction[i][1] * 2;
if (data.inArea(newX, newY) &&
!data.visited[newX][newY]) {
setData(x + direction[i][0], y + direction[i][1]);
go(newX, newY);
}
}
}
這裡要注意每兩個格子之間的差距是2,因為中間都隔着一堵牆。go的參數是開始的參數,開始不能直接從入口開始,因為入口是我們新加的,不符合迷宮節點的規矩,比如每一個格子相差兩個點,但是出口和第一個點差一個而已。
int newX = x + direction[i][0] * 2;
int newY = y + direction[i][1] * 2;
乘上2的原因就是因為兩個格子之間相差了2。而渲染都放在了setData裡面處理。渲染的點就不是我們newX和newY了,因為那兩個點本來就是road,渲染的應該是兩個點之間的牆,是以是加1的。和前面深度搜尋對比差別就是,這裡沒有終止點,不是到了exit就退出,事實上是不一定有解的。因為我們這裡是要全部生成而不是生成到了終點就停止,是以是無終止條件的。但是for循環裡面是隐含了的。還有一個就是條件确認是不是一條路,這個決策是不必要的,因為就要生成路的。但是這樣導緻的迷宮很無随機性:
因為方向都是一樣的,從左上右下這樣。
這是遞歸方法,非遞歸方法:
private void go_iterator(){
Stack<Position> stack = new Stack<>();
Position firstPosition = new Position(data.getEntranceX(), data.getEntranceY() + 1);
stack.push(firstPosition);
data.visited[firstPosition.getX()][firstPosition.getY()] = true;
while (!stack.isEmpty()){
Position position = stack.pop();
for (int i = 0; i < 4; i++) {
int newX = position.getX() + direction[i][0] * 2;
int newY = position.getY() + direction[i][1] * 2;
if (data.inArea(newX, newY) &&
!data.visited[newX][newY]) {
setData(position.getX() + direction[i][0], position.getY() + direction[i][1]);
stack.push(new Position(newX, newY));
data.visited[newX][newY] = true;
}
}
}
}
不一樣的原因就是因為在加入棧的時候就已經上下左右看了,看看能不能走,走就直接把牆消去了,是以會出現鋸齒型。至于大體的trend的不一樣的因為兩個方向是相反的。
廣度周遊:之前提到過了和深度周遊差不多:
private void go_level(){
LinkedList<Position> stack = new LinkedList<>();
Position firstPosition = new Position(data.getEntranceX(), data.getEntranceY() + 1);
stack.addLast(firstPosition);
data.visited[firstPosition.getX()][firstPosition.getY()] = true;
while (stack.size() != 0){
Position position = stack.removeFirst();
for (int i = 0; i < 4; i++) {
int newX = position.getX() + direction[i][0] * 2;
int newY = position.getY() + direction[i][1] * 2;
if (data.inArea(newX, newY) &&
!data.visited[newX][newY]) {
setData(position.getX() + direction[i][0], position.getY() + direction[i][1]);
stack.addLast(new Position(newX, newY));
data.visited[newX][newY] = true;
}
}
}
}
生成的圖像都很規則。 一個很重要的原因的因為我們在資料結構的選擇過程中都是棧和隊列,可預期性太強了。我們隻需要在資料結構中加上随機性就好了。出隊或者是删除都是随機隊列。
public class RandomQueue<E> {
private ArrayList<E> queue;
public RandomQueue() {
queue = new ArrayList<>();
}
public void add(E e) {
queue.add(e);
}
public E remove() {
if (queue.size() == 0) {
throw new IllegalArgumentException("no elements!");
}
int randomIndex = (int) (Math.random() * queue.size());
E Ele = queue.get(randomIndex);
queue.set(randomIndex, queue.get(queue.size() - 1));
queue.remove(queue.size() - 1);
return Ele;
}
public boolean isEmpty(){
return queue.isEmpty();
}
}
在廣度優先裡面把隊列改一下:
這樣就有一定的随機性了。可以看到在很多空白的小格子很容易讓别人猜到我們是怎麼生成的。是以可以加上如果沒有周遊到的格子全部變黑色。
private void go_level(){
RandomQueue<Position> stack = new RandomQueue<>();
Position firstPosition = new Position(data.getEntranceX(), data.getEntranceY() + 1);
stack.add(firstPosition);
data.openMinst(firstPosition.getX(), firstPosition.getY());
data.visited[firstPosition.getX()][firstPosition.getY()] = true;
while (!stack.isEmpty()){
Position position = stack.remove();
for (int i = 0; i < 4; i++) {
int newX = position.getX() + direction[i][0] * 2;
int newY = position.getY() + direction[i][1] * 2;
if (data.inArea(newX, newY) &&
!data.visited[newX][newY]) {
data.openMinst(newX, newY);
setData(position.getX() + direction[i][0], position.getY() + direction[i][1]);
stack.add(new Position(newX, newY));
data.visited[newX][newY] = true;
}
}
}
}
但是其實還有一個問題,很多時候這個迷宮的路徑順序是都是斜向下的趨勢,是以有時候是可以猜到怎麼走的。可以通過改進随機隊列:
public void add(E e) {
if (Math.random() < 0.5){
queue.addFirst(e);
}else {
queue.addLast(e);
}
}
public E remove() {
if (queue.size() == 0) {
throw new IllegalArgumentException("no elements!");
}
// int randomIndex = (int) (Math.random() * queue.size());
// E Ele = queue.get(randomIndex);
// queue.set(randomIndex, queue.get(queue.size() - 1));
// queue.remove(queue.size() - 1);
// return Ele;
if (Math.random() < 0.5){
return queue.removeFirst();
}else {
return queue.removeLast();
}
}
這個時候随機性就更強了:
掃雷
開始的時候,會展開一片區域,這片區域随機找一個點點開,如果沒有雷,那麼就會展開一片區域,雷的個數是固定的。有些展開的地方會有數字,那麼就表面這個地方的周圍八個格子裡面有多少個雷。
格子和雷都使用圖檔表示。
public static void putImage(Graphics2D graphics2D, int x, int y, String imageURL) {
ImageIcon imageIcon = new ImageIcon(imageURL);
Image image = imageIcon.getImage();
graphics2D.drawImage(image, x, y, null);
}
在frame面版畫上:
int w = canvasWidth / data.getM();
int h = canvasHeight / data.getN();
for (int i = 0; i < data.getN(); i++) {
for (int j = 0; j < data.getM(); j++) {
if (data.isMine(i, j)){
AlgorithmHelper.putImage(graphics2D, j * w, i * h, MineSweeperData.mineImageURL);
}else {
AlgorithmHelper.putImage(graphics2D, j * w, i * h, MineSweeperData.blockImageURL);
}
}
}
}
測試一下。
随機雷區
首先是如何在掃雷區域中随機分布若幹個雷。我們要做的事情是要在雷區裡面随機配置設定雷。做法很簡單,就是x,y随機即可。
private void generateMines(int number) {
for (int i = 0; i < number; i++) {
while (true) {
int x = (int) (Math.random() * N);
int y = (int) (Math.random() * M);
if (!mines[x][y]) {
mines[x][y] = true;
break;
}
}
}
}
這樣其實是比較可行的,但是因為有一個死循環,如果盤面小,而且雷多的話,生成時間可能會很慢,因為生成相同區域的雷區就會很密集。為了避免出現這種情況,可以先生成,再排序。
for (int i = 0; i < number; i++) {
int x = i / M;
int y = i % M;
mines[x][y] = true;
}
int swapTime = 100;
for (int j = 0; j < swapTime; j++) {
int x1 = (int) (Math.random() * N);
int y1 = (int) (Math.random() * M);
int x2 = (int) (Math.random() * N);
int y2 = (int) (Math.random() * M);
swap(x1, y1, x2, y2);
}
這樣得到的結果很明顯還不夠随機,因為前面兩行的雷區太多了,有時候随機交換不到上面的行數。可以調大交換的次數。或者更保險的方法就是每一個空間都進行随機交換一次,這樣效果更好。其實這個就類似于洗牌算法,使得洗牌算法的結果能不能足夠亂。比如我們隊54張撲克牌進行洗牌,那麼就有54!種結果。一個好的洗牌算法就是要等機率的獲得54!種算法。
首先有一個問題,就是如何驗證一個算法足夠亂。可以使用蒙特卡洛方法來驗證,使用大樣本的結果來驗證。
有一種等概論的方法,首先使用随機算法從54張牌抽一張放在第一個位置,然後繼續餘下步驟。如果要維護每一個元素的抽取的可能性是等價的,就需要保留已經抽取元素的位置,這樣如果剩下的元素少了,那麼抽取到的可能性就會很低。
Fisher-Yates算法
首先把是以的元素都放在一個空間裡,然後随機一個元素,把随機出來的這個元素和第一個元素交換位置,那麼第一個元素就完成了;接着在剩下的位置繼續選擇,然後和第二個位置繼續交換,以此類推。
int swapTime = N * M;
for (int j = swapTime - 1; j >= 0; j--) {
int x1 = j / M;
int y1 = j % M;
int rangeNumber = (int) (Math.random() * (j + 1));
int x2 = rangeNumber / M;
int y2 = rangeNumber % M;
swap(x1, y1, x2, y2);
}
在這裡需要把一維坐标轉換成二維坐标,其他的就和上述一樣。這個時候得到的結果随機性不減,而且沒有死循環,時間上快了不少。
互動
加入滑鼠互動,隻需要在控制層添加滑鼠左右鍵判斷即可。
private class AlgoMouseListener extends MouseAdapter {
@Override
public void mouseClicked(MouseEvent event) {
event.translatePoint(-(int) (frame.getBounds().width - frame.getCanvasWidth()), -(int) (frame.getBounds().height - frame.getCanvasHeight()));
Point point = event.getPoint();
int w = frame.getCanvasWidth() / data.getM();
int h = frame.getCanvasHeight() / data.getN();
int x = point.y / h;
int y = point.x / w;
if (SwingUtilities.isLeftMouseButton(event)) {
System.out.println(x + " " + y);
setData(true, x, y);
} else if (SwingUtilities.isRightMouseButton(event)) {
setData(false, x, y);
}
}
}
private void setData(boolean isLeft, int x, int y) {
if (data.inArea(x, y)) {
if (isLeft) {
data.open[x][y] = true;
} else {
data.flags[x][y] = !data.flags[x][y];
}
}
frame.render(data);
AlgorithmHelper.pause(DELAY);
}
現在點選隻是會展開一個點,但實際上一個展開一片區域的。但是這個區域是不規則的,它的邊界是數字區域,也就是說如果目前的區域是數字,那麼就停止了,如果不是,那麼就會向外擴充。
FloodFill算法
比如現在有一個圖形,從某一點開始擴張直到邊界為止。這個填充方法其實就很像深度周遊或者廣度周遊這樣。
public void open(int x, int y) {
if (inArea(x, y) && !isMine(x, y)) {
open[x][y] = true;
if (numbers[x][y] > 0) {
return;
} else {
for (int i = x - 1; i <= x + 1; i++) {
for (int j = y - 1; j <= y + 1 ; j++) {
if (inArea(i, j) && !open[i][j] && !mines[i][j]){
open(i, j);
}
}
}
}
}
}
對上下左右斜方向的八個格子進行周遊搜尋。
基本的掃雷核心操作就全部完成了。
分形圖的繪制
首先,分形圖指在這個圖案上右自相似的部分。
每一個分支和樹本身是很相似的,可以看的出其實就是一個遞歸結構。
Vicsek Fractal
正方形的九宮格分形。每一次切分隻對中間和四個角落的正方形做繪制,這樣遞歸繪制下去。模闆還是使用之前的swing繪畫。
public class FractalData {
private int depth;
public FractalData(int depth){
this.depth = depth;
}
public int getDepth(){
return depth;
}
}
所有的繪畫邏輯都在frame繪畫裡面。
public void drawFractal(Graphics2D graphics2D, int x, int y, int w, int h, int depth) {
if (depth == data.getDepth()) {
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Indigo);
AlgorithmHelper.fillRectangle(graphics2D, x, y, w, h);
return;
}
if (w <= 1 || h <= 1) {
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Indigo);
AlgorithmHelper.fillRectangle(graphics2D, x, y, Math.max(w, 1), Math.max(h, 1));
return;
}
int w_3 = w / 3;
int h_3 = h / 3;
drawFractal(graphics2D, x, y, w_3, h_3, depth + 1);
drawFractal(graphics2D, x + 2 * w_3, y, w_3, h_3, depth + 1);
drawFractal(graphics2D, x + w_3, y + h_3, w_3, h_3, depth + 1);
drawFractal(graphics2D, x, y + 2 * h_3, w_3, h_3, depth + 1);
drawFractal(graphics2D, x + 2 * w_3, y + 2 * h_3, w_3, h_3, depth + 1);
}
這段代碼加入到frame的paintComponent即可。可以看到遞歸繪畫裡面隻有邊界條件才畫,也就是說隻有當分到了不可再分的時候才會畫,是以無論是多少層都是畫一些小點點。
這樣看不出主要的效果,我們需要的是固定視窗大小,然後正方形的大小與視窗所一緻。
是以需要改變一下,傳入的參數就是最大的深度,通過鍵盤來調整深度即可。其實畫的正方形有多大是有那幾個邊界條件覺定的:
if (depth == data.getDepth()) {
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Indigo);
AlgorithmHelper.fillRectangle(graphics2D, x, y, w, h);
return;
}
if (w <= 1 || h <= 1) {
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Indigo);
AlgorithmHelper.fillRectangle(graphics2D, x, y, Math.max(w, 1), Math.max(h, 1));
return;
}
是以隻需要改變深度即可。
private class AlgoKeyListener extends KeyAdapter {
@Override
public void keyReleased(KeyEvent keyEvent) {
if (keyEvent.getKeyChar() >= '0' &&
keyEvent.getKeyChar() <= '9') {
int depth = keyEvent.getKeyChar() - '0';
setData(depth);
}
}
}
設定一個鍵盤輸入,輸入數字就改變深度即可。
可以根據想要的形狀調整frame的畫圖函數即可:
Sierpinski carpet
這種分形和前面的性質有所不同,第一層是有一個大的正方形,第二層就會出現小正方形包圍着大正方形,下一層就會出現更小的正方形。
其他的都不用變,隻需要改一下frame的paint函數即可。
int w_3 = w / 3;
int h_3 = h / 3;
if (depth == data.getDepth()) {
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Amber);
AlgorithmHelper.fillRectangle(graphics2D, x + w / 3, y + h / 3, w / 3, h / 3);
return;
}
if (w <= 1 || h <= 1) {
return;
}
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (i == 1 && j == 1) {
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Amber);
AlgorithmHelper.fillRectangle(graphics2D, x + w / 3, y + h / 3, w / 3, h / 3);
} else {
drawFractal(graphics2D, x + i * w_3, y + j * h_3, w_3, h_3, depth + 1);
}
}
}
特殊情況,到了遞歸層數之後就不需要畫小正方形了,隻需要畫中間的大正方形即可,如果長和寬太小畫不下去,那麼不需要畫,因為就算是畫中間的大正方形也看不見,因為是要整數。接下來的兩層循環,1,1的情況就是大正方形中間的情況,直接畫,其他的就遞歸畫周邊小的即可。
把正方形換成其他形狀也是可以的。
Siepinski Triangle
把一個大三角形分成四個,中間的一個三角形不做繪制。
其實和之前是一樣的,隻是繪畫方式不一樣:
public void drawFractal_Triangle(Graphics2D graphics2D, int Ax, int Ay, int size, int depth) {
if (size <= 1) {
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Lime);
AlgorithmHelper.fillRectangle(graphics2D, Ax, Ay, 1, 1);
return;
}
int Bx = Ax + size;
int By = Ay;
int h = (int) (Math.sin(60.0 * Math.PI / 180.0) * size);
int Cx = Ax + size / 2;
int Cy = Ay - h;
if (depth == data.getDepth()) {
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Cyan);
AlgorithmHelper.fillTriangle(graphics2D, Ax, Ay, Bx, By, Cx, Cy);
return;
}
int AB_centerX = (Ax + Bx) / 2;
int AB_centerY = (Ay + By) / 2;
int AC_centerX = (Ax + Cx) / 2;
int AC_centerY = (Ay + Cy) / 2;
int BC_centerX = (Bx + Cx) / 2;
int BC_centerY = (By + Cy) / 2;
drawFractal_Triangle(graphics2D, Ax, Ay, size / 2, depth + 1);
drawFractal_Triangle(graphics2D, AC_centerX, AC_centerY, size / 2, depth + 1);
drawFractal_Triangle(graphics2D, AB_centerX, AB_centerY, size / 2, depth + 1);
}
首先是求出高,用高來求得這三個點的左邊,A點是三角形的左下角的坐标,然後逆時針依次是ABC。
Koch Snowflake
繪出雪花形狀的分形圖。
這是在水準時候的情況,如果是傾斜有角度的,隻需要加上角度即可。
上面那張手繪的圖檔是基礎形狀。首先是視窗的長度和寬度,由于60度,寬度就是3倍的side,高的話比side*sin(60)大就好了。要遞歸畫四條線:
public void drawSnow(Graphics2D graphics2D, double x1, double y1, double side, double angle, int depth) {
if (side <= 0) {
return;
}
if (depth == data.getDepth()) {
double x2 = x1 + side * Math.cos(angle * Math.PI / 180.0);
double y2 = y1 - side * Math.sin(angle * Math.PI / 180.0);
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.DeepOrange);
AlgorithmHelper.drawLine(graphics2D, x1, y1, x2, y2);
return;
}
double side_3 = side / 3;
double x2 = x1 + side_3 * Math.cos(angle * Math.PI / 180.0);
double y2 = y1 - side_3 * Math.sin(angle * Math.PI / 180.0);
drawSnow(graphics2D, x1, y1, side_3, angle, depth + 1);
double x3 = x2 + side_3 * Math.cos((angle + 60.0) * Math.PI / 180.0);
double y3 = y2 - side_3 * Math.sin((angle + 60.0) * Math.PI / 180.0);
drawSnow(graphics2D, x2, y2, side_3, angle + 60, depth + 1);
double x4 = x3 + side_3 * Math.cos((angle - 60.0) * Math.PI / 180.0);
double y4 = y3 - side_3 * Math.sin((angle - 60.0) * Math.PI / 180.0);
drawSnow(graphics2D, x3, y3, side_3, angle - 60, depth + 1);
drawSnow(graphics2D, x4, y4, side_3, angle, depth + 1);
return;
}
分别求出起始點即可,不需要求終點,因為side就是長度,可以求得終點。
最後的效果:
draw a tree
畫出的樹肯定是有一定規律的樹了,首先是從一條豎直的直線展開,然後一層一層按照某種角度展開,最後形成一條直線。整體上,第一層就是繪制一條直線;來到第一層的時候就會分叉,下半部分不變,上半部分再次分叉。
再分叉的過程中,兩邊對稱的話,左邊就是a度,右邊就是-a度。
如果分叉點是(x,y),那麼左端點就是(x - ssin(a), y - s * cos(a)),右半部分也是一樣(x-ssin(-a), y - s* cos(-a)),和之前的雪花是一樣的,需要累積這個偏差的角度。
可以看的出,這棵樹是由兩部分組成的,樹幹和樹,是以繪畫肯定不能再遞歸終止條件裡面的了。
double side_2 = side / 2;
if (side_2 <= 0) {
return;
}
if (depth == data.getDepth()) {
double x2 = x1 - side * Math.cos(angle * Math.PI / 180.0);
double y2 = y1 - side * Math.sin(angle * Math.PI / 180.0);
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Green);
AlgorithmHelper.drawLine(graphics2D, x1, y1, x2, y2);
return;
}
遞歸終止條件,就是畫葉子的了,按照一定的角度展開,angle是上面傳過來的參數。之後就是正式遞歸:
double x2 = x1 - side / 2 * Math.cos(angle * Math.PI / 180.0);
double y2 = y1 - side / 2 * Math.sin(angle * Math.PI / 180.0);
AlgorithmHelper.setColor(graphics2D, AlgorithmHelper.Brown);
AlgorithmHelper.drawLine(graphics2D, x1, y1, x2, y2);
畫樹幹,和上面的其實是一樣的,但是顔色不同而已。
drawTree(graphics2D, x2, y2, side / 2, angle + data.splitAngle / 2, depth + 1);
drawTree(graphics2D, x2, y2, side / 2, angle - data.splitAngle / 2, depth + 1);
之後就是畫分支的遞歸了,分支遞歸的角度是有一定變化的,左邊變化多少,右邊多少可以自己指定,然後層數加一。上面的公式在和上圖給出的角度不太一樣,是因為上圖的是垂直角度,而在計算的時候是水準角度。可以依照這個原理畫一些其他的樹。