前情提要——二叉樹
二叉樹之前已經提到過,二叉樹這種資料結構隻能有兩個子數,一左一右。
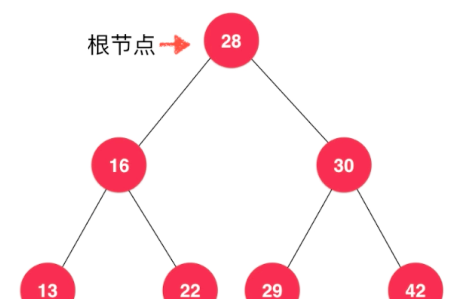
葉子節點就是左右孩子都是空的,但是并不是每一顆樹都像上圖所示的那樣這麼規整,有些樹樹可以隻有左孩子沒有右孩子的。二叉樹的節點一定會大于左節點的值小于右節點的值,每一個節點都要滿足,所有每一個節點下面拿出來的樹都可以作為一個二叉樹。既然有大于等于了,那麼這科樹的元素一定要有可比較性才可以。
Create a BST
package Tree.BST;
public class BST<E extends Comparable<E>> {
/**
* Binary Search Tree
*/
private class Node {
public E e;
public Node left, right;
public Node(E e) {
this.e = e;
left = right = null;
}
}
private Node root;
private int size;
public BST() {
root = null;
size = 0;
}
public int size(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
}
和上面描述的基本一緻的。
Insert an element
插入一個元素也很簡單,檢視目前元素是否是大于或者小于節點元素,如果是大于,那麼就右邊遞歸即可,二叉樹的插入非遞歸寫法和連結清單很像。
public void add(E e) {
root = add(root, e);
}
private Node add(Node node, E e) {
if (node == null) {
size++;
return new Node(e);
}
if (e.compareTo(node.e) < 0) {
node.left = add(node.left, e);
} else {
node.right = add(node.right, e);
}
return node;
}
Select an element
判斷一個元素和查找一個元素算法基本一緻,小于左邊找,大于右邊找即可。
···
public boolean contains(E e) {
return contains(root, e);
}
public boolean contains(Node node, E e) {
if (node == null) {
return false;
} else if (e.equals(node.e)) {
return true;
} else if (e.compareTo(node.e) < 0) {
return contains(node.left, e);
} else {
return contains(node.right, e);
}
}
Traversal
前中後序周遊都很簡單,代碼和前面C++都都是一樣的。對于中序周遊的非遞歸周遊。非遞歸周遊可以對比遞歸來實作,資料結構裡面有遞歸屬性的隻有棧了,是以可以用棧來實作。先把根元素壓進棧,由于前序周遊直接輸出第一個周遊到到元素,是以先出棧輸出之後再把出棧的元素的子節點壓進去,要注意的是右孩子先壓,左孩子再壓,因為周遊的順序是先周遊左邊再周遊右邊,以此類推,隻到空為止。
遞歸處理很簡單,幾行就好了,主要繁瑣到就是非遞歸周遊到過程,前序周遊的非遞歸。這個算算比較簡單到,因為先周遊到是一開始周遊到到點,再依次是左右子樹,沒有倒叙過程,都是有順序性到,是以可以直接用棧處理,先把跟節點扔進去,如果棧不為空,那麼就要出棧,直接輸出目前元素,在放入左右子樹即可,但是放入左右子樹需要注意,應當先放入右子樹再放入左子樹,因為是先周遊左子樹再周遊右子樹,而棧是反過來的。
public void preOrderNonRecur() {
Stack<Node> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
Node node = stack.pop();
System.out.print(node.e + " ");
if (node.right != null)
stack.push(node.right);
if (node.left != null)
stack.push(node.left);
}
System.out.println();
}
這就是前序周遊。中序的非遞歸周遊就有點複雜了,中序周遊是左中右,這個時候順序就不是都往下了,沒有辦法一次性就周遊完,棧裡面一開始存儲都應該是周遊一開始要拿出來輸出都元素,是以可以先把左邊子樹都周遊完存到棧裡面,然後以這些存到棧裡面的元素為起點周遊下去。每次出來一個元素都要看看這個元素的右子樹是否存在,如果存在就要周遊,但其實不必要這樣判斷,因為算法前面的大循環已經判斷了。
public void inOrderNonRecur() {
Stack<Node> stack = new Stack<>();
Node node = root;
while (node != null || !stack.isEmpty()) {
while (node != null) {
stack.push(node);
node = node.left;
}
if (!stack.isEmpty()) {
Node node1 = stack.pop();
System.out.print(node1.e + " ");
node = node1.right;
}
}
System.out.println();
對于後序周遊就是最複雜的了,由于後序周遊和前序周遊都是逆的,是以一開始也要先把左子樹放到棧裡面,出的時候在看看有沒有右子樹。但是這裡有個問題,這裡的右子樹是先輸出再到目前節點的,首先要拿到目前節點,然後再看看右子樹有沒有,有就周遊,等右子樹周遊完之後目前節點還在棧裡面,這個時候再拿出來的還是目前節點,這個時候就不知道右子樹有沒有被周遊過了,這就進入到了一個死循環,是以這裡要使用一個标記來看看有沒有通路了右子樹,如果通路了右子樹,就可以放心輸出了,因為while循環的時候已經到了最左邊的了,這個時候不會再有左子樹,隻需要考慮右子樹即可。
public void lastOrderNonRecur() {
Stack<Node> stack = new Stack<>();
Node node = root;
while (node != null || !stack.isEmpty()) {
while (node != null) {
stack.push(node);
node = node.left;
}
if (!stack.isEmpty()) {
Node node1 = stack.peek();
if (!node1.isright) {
node1.isright = true;
node = node1.right;
} else {
node = stack.pop();
System.out.print(node.e + " ");
node = null;
}
}
}
System.out.println();
}
中序周遊和後序周遊都從左邊擴散到右邊。
最後一個就是層序周遊,層序周遊就是廣度優先周遊,實作用隊列就好了,事實上大多數的廣度優先周遊基本都是要使用隊列的。之前的資料結構說過,直接給出代碼即可:
levelOrder(){
Queue<Node> nodes = new LinkedList<>();
nodes.add(root);
while (!nodes.isEmpty()){
Node node = nodes.remove();
System.out.print(node.e + " ");
if (node.left != null){
nodes.add(node.left);
}
if (node.right != null){
nodes.add(node.right);
}
}
System.out.println();
}
remove an specific element
删除一個元素有點麻煩,如果隻有一邊有元素,那麼就隻需要把一邊的移動上去替代即可,如果兩邊都有子樹,那麼就需要把右子樹最小的一個移動上去,當然,其實也可以把左子樹最大的移動上去,替代原來的即可。
private Node remove(Node node, E e) {
if (node == null) {
return null;
} else if (e.compareTo(node.e) < 0) {
node.left = remove(node.left, e);
return node;
} else if (e.compareTo(node.e) > 0) {
node.right = remove(node.right, e);
return node;
} else{
if (node.left == null){
Node node1 = node.right;
node.right = null;
size--;
return node1;
}else if (node.right == null){
Node node1 = node.left;
node.left = null;
size--;
return node1;
}else {
Node successor = new Node(minimum(node.right).e);
successor.left = node.left;
successor.right = removeMin(node.right);
node.left = node.right = null;
return successor;
}
}
}
集合Set
集合這種資料結構有點像高中數學那種集合,集合有一個特點,就是每一個元素隻能有一個,這個性質可以用來做去重工作。再上面實作的二分搜尋樹是不可以存放重複資料的,是以可以作為集合的一種底層實作方式。二叉樹的實作是有要求的,要求一定要是二叉樹的結構來實作,而集合隻是要求有這麼多功能就OK,是以集合屬于一種進階資料結構,沒有具體實作方法。
集合基本方法
Set建立一個集合,remove移除集合的一個元素,contains檢視集合是否包含這個元素,getSize獲得集合大小,isEmpty檢視集合是否為空,add添加一個元素,不能添加重複的元素。
集合的應用很廣,通路量的統計,詞彙量的統計等等都可以用到集合去重。首先是基于BST的集合,上面實作的BST完全包含了集合的功能。直接包裝一下即可。
Leecode804
Leecode804,摩斯碼的判斷:
這個題目非常簡單,直接替換一下扔到集合裡面就好了,這裡使用的就是treeSet,是使用的紅黑樹實作方式:
class Solution {
public int uniqueMorseRepresentations(String[] words) {
String [] codes = {".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."};
TreeSet<String> set = new TreeSet<>();
for (String word : words){
StringBuilder stringBuilder = new StringBuilder();
for (int i = 0; i < word.length(); i++) {
stringBuilder.append(codes[word.charAt(i) - 'a']);
}
set.add(stringBuilder.toString());
}
return set.size();
}
}
之前所實作的集合,二分搜尋樹,紅黑樹這些實作的集合都是有順序性的,因為這些結構實作的集合是很容易可以排序(中序周遊),找到下一個上一個等等,是屬于有序集合,而連結清單這些就屬于無序性的了。
優先隊列和堆
堆的基本結構, 這裡的堆實作也和樹有關系,二叉堆。二叉堆是一個完全二叉樹。
package Heap;
import Array.Array;
public class MaxHeap<E extends Comparable<E>> {
private Array<E> data;
public MaxHeap(int capacity) {
data = new Array<E>(capacity);
}
public MaxHeap() {
data = new Array<E>();
}
public int size() {
return data.getSize();
}
public boolean isEmpty() {
return data.isEmpty();
}
private int parent(int index) {
if (index == 0) {
throw new IllegalArgumentException("No parents when index equal zero!");
}
return (index - 1) / 2;
}
private int leftChild(int index) {
return index * 2 + 1;
}
private int rightChild(int index) {
return index * 2 + 2;
}
}
堆的實作之前的C++有寫過,對于插入一個元素,插入在數組的最後面,然後再按照規則慢慢的shiftUp上去,如果這個元素是大于它的父母,那麼就要浮上去,然後以父母為目前元素繼續循環判斷:
private void shiftUp(int index) {
while (index > 0 && data.get(index).compareTo(data.get(parent(index))) > 0) {
data.swap(index, parent(index));
index = parent(index);
}
}
輸出最大值的元素就隻需要把第一個元素輸出,把最後一個元素補上,再把新的第一個元素進行shiftDown操作:
private void shiftDown(int index){
while (leftChild(index) < data.getSize()){
int j = leftChild(index);
if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0){
j = rightChild(index);
}
if (data.get(index).compareTo(data.get(j)) >= 0){
break;
}
data.swap(index, j);
index = j;
}
}
堆還有一個replace操作,取出最大值,用另一個值替代,可以先輸出最大值,然後再添加另一個值,但是這樣這樣複雜度就是
。可以直接用新的元素替換最大值,然後做shiftDown操作即可。
public E replace(E e) {
E max = data.get(0);
data.set(0, e);
shiftDown(0);
return max;
}
如果存在一個數組,想要直接在數組上操作,使得這個數組直接變成一個堆,那就需要heapify操作了。從最後一個葉子節點開始不斷做shiftdown操作即可:
for (int i = parent(this.data.getSize() - 1); i >= 0; i --){
shiftDown(i);
}
基于堆的優先隊列就很簡單了,出隊列的時候就直接extract最大值即可。
優先隊列347
給定一個數組,數組元素可以重複,那麼數字就會出現重複這個問題,在這種情況下,就需要求出前N個頻率最高的元素,這就有點像優先隊列了。先用Treemap把頻率存儲到樹裡面,然後放到優先隊列裡面輸出即可:
package Queue.Leecode347;
import java.util.LinkedList;
import java.util.List;
import java.util.PriorityQueue;
import java.util.TreeMap;
class Solution {
private class Freq implements Comparable<Freq>{
int e, freq;
public Freq(int e, int freq){
this.e = e;
this.freq = freq;
}
@Override
public int compareTo(Freq another) {
if (this.freq < another.freq){
return -1;
}
else if (this.freq > another.freq){
return 1;
}else {
return 0;
}
}
}
public List<Integer> topKFrequent(int[] nums, int k) {
TreeMap<Integer, Integer> map = new TreeMap<>();
for (int n : nums) {
if (map.containsKey(n)) {
map.put(n, map.get(n) + 1);
} else {
map.put(n, 1);
}
}
PriorityQueue<Freq> priorityQueue = new PriorityQueue<>();
for(int key: map.keySet()){
if(priorityQueue.size() < k)
priorityQueue.add(new Freq(key, map.get(key)));
else if(map.get(key) > priorityQueue.peek().freq){
priorityQueue.remove();
priorityQueue.add(new Freq(key, map.get(key)));
}
}
List<Integer> linkedList = new LinkedList<>();
while (!priorityQueue.isEmpty()){
linkedList.add(priorityQueue.remove().e);
}
return linkedList;
}
public static void main(String[] args) {
int[] nums = {1,1,1,2,2,3};
Solution solution = new Solution();
System.out.println(solution.topKFrequent(nums, 2));
}
}
并查集
之前包括前面部落格所讨論的樹問題都是樹問題,這些樹問題都是由父親指向孩子,而這個并查集是孩子指向樹,可以由孩子找到跟節點。并查集可以用來回答連接配接問題。給出兩個點,看看這兩個點是否是連接配接的。前面部落格提到的就是找到根然後比較兩個根是不是一樣的即可。這裡的并查集主要實作兩個操作,Union和isConnected,連接配接兩個節點和檢視兩個節點是否是連接配接的。
并查集Quick Find
每個元素的下标都會有一個标記,如果标記相同那麼就是同一個類别,也就是連接配接在了一起。一開始每一個數字就是一個類别,是以一開始下标都是不一樣的。
private int find(int p) {
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of range!");
}
while (p != parent[p]) {
p = parent[p];
}
return p;
}
@Override
public int getSize() {
return parent.length;
}
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
@Override
public void unionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot){
return;
}
parent[pRoot] = qRoot;
}
這種情況下的的查找複雜度是很快的,但是合并就很慢了,需要
的複雜度。
基于樹的Quick union
每一個節點都指向上一個節點,最後指向的就是根,根的parent就是他自己,如果根相同,那麼這兩個節點就是相同的。
private int find(int p) {
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of range!");
}
while (p != parent[p]) {
p = parent[p];
}
return p;
}
@Override
public int getSize() {
return parent.length;
}
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
@Override
public void unionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot){
return;
}
parent[pRoot] = qRoot;
}
合并的時候直接把根節點合并就好了。但是這種合并有個弊端,如果合并的時候恰好把大的哪一組資料合并到了小的哪一組資料上,就容易出現類似連結清單那樣長長的資料段,這個時候就可以先做判斷,看看哪一邊的資料量大就把小資料的合并到大的一邊去即可。是以就需要一個記錄數量的數組。
@Override
public void unionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
if (sz[pRoot] < sz[qRoot]) {
parent[pRoot] = qRoot;
sz[qRoot] += sz[pRoot];
}else {
parent[qRoot] = pRoot;
sz[pRoot] += sz[qRoot];
}
}
其他都是一樣的。這樣其實不太嚴謹,如果資料都是分散開的,那麼就應該反着過來,是以應該以高度作為對比的條件:
@Override
public void unionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
if (rank[pRoot] < rank[qRoot]){
parent[pRoot] = qRoot;
}else if (rank[pRoot] > rank[qRoot]){
parent[qRoot] = pRoot;
}else {
parent[qRoot] = pRoot;
rank[pRoot] += 1;
}
路徑壓縮 Path Compression
如果這個并查集已經被壓縮成了長條型,就需要使用路徑壓縮來優化了:
這種情況下就隻需要指向父親的父親即可,隻要加上一行代碼就可以。
private int find(int p) {
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of range!");
}
while (p != parent[p]) {
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
哈希表HashTable
首先看一個簡單的問題:
傳回第一個不重複的字元。最簡單的處理方式就是使用一個映射,先計算一遍所有字元的頻率是多少,然後再周遊一遍所有的字元,看看第一個字元出現次數為一是索引下标是多少即可。
但是這樣比較麻煩,我們可以使用一個數組包含了二十六個字母。
class Solution {
public int firstUniqChar(String s) {
int[] freq = new int[26];
for (int i = 0; i < s.length(); i++) {
freq[s.charAt(i) - 'a']++;
}
for (int i = 0; i < s.length(); i++) {
if (freq[s.charAt(i) - 'a'] == 1) {
return i;
}
}
return -1;
}
}
在這個問題就隐藏着哈希表這種資料結構。上面的frequency數組就是一個哈希表,每一個字元都和一個索引對應。數組的查找是支援下表操作的,所有複雜度可以是
的複雜度。哈希其實就是使用一個下标來訓示一個數值或者是字元,然後解決哈希沖突。簡單的來說,哈希就展現了用空間換時間的思想。
鍵通過哈希函數得到的索引分布越均勻越好。對于一些特殊的領域,有特殊領域的哈希函數設計方式甚至有專門的論文。
首先是整型哈希函數的設計,小範圍整數直接使用,負整數就要進行偏移。對于大整數,就需要對這個大整數進行處理,使得變成一個計算機可以處理的資料。常用的方法就是取模了。但是有時候取模使得分布不會有均勻的分布,是以可以使用素數作為取模數值。
對于字元串的處理,就需要轉成整型處理
在Java裡面的HashCode是以整型為基準的,他隻是給出了hashcode,索引下标還是需要其他的計算。
hash沖突——鍊位址法
如果沒有沖突,那麼就按照下标直接存放,如果産生了沖突,也就是一個索引下有兩個相同的哈希值,那麼就用連結清單把他們都串起來,如果還是有相同的那麼繼續接上,是以每一個空間等于是存上了一個連結清單,也就是一個查找表,既然是查找表那麼久不一定是連結清單了,可以是樹結構,紅黑樹二叉樹都可以。在Java8之前,一直都是一個位置對應一個連結清單,Java8開始如果沖突達到了一定程度,也就是連結清單裡面元素過多了,那麼就會把每一個位置自動轉成紅黑樹。因為如果在資料量少的情況下,使用連結清單查找是更加快的,因為沒有紅黑樹的維護過程,而資料量多的時候就需要使用紅黑樹了。
public class Hash_Table<K, V> {
private TreeMap<K, V>[] hashtable;
private int M;
private int size;
public Hash_Table(int M) {
this.M = M;
size = 0;
hashtable = new TreeMap[M];
for (int i = 0; i < hashtable.length; i++) {
hashtable[i] = new TreeMap<>();
}
}
public Hash_Table() {
this(97);
}
private int hash(K key) {
return (key.hashCode() & 0x7fffffff) % M;
}
public int getSize() {
return size;
}
public void add(K key, V value) {
if (hashtable[hash(key)].containsKey(key)) {
hashtable[hash(key)].put(key, value);
} else {
hashtable[hash(key)].put(key, value);
size++;
}
}
public V remove(K key){
TreeMap<K, V> treeMap = hashtable[hash(key)];
V ret = null;
if (treeMap.containsKey(key)){
ret = treeMap.remove(key);
size--;
}
return ret;
}
public void set(K key, V value){
TreeMap<K, V> treeMap = hashtable[hash(key)];
if (!treeMap.containsKey(key)){
throw new IllegalArgumentException("no element!");
}else {
treeMap.put(key, value);
}
}
public boolean contains(K key){
return hashtable[hash(key)].containsKey(key);
}
public V get(K key){
return hashtable[hash(key)].get(key);
}
}
每一個位置都使用紅黑樹,插入的資料帶鍵值和資料,根據鍵值取哈希值然後求餘。過程很簡單。如果插入的資料是N個,哈希表大小是M,如果每一個位置是連結清單的話,那麼平均複雜度就是
,如果是平衡樹就是
。可以看到這個複雜度并沒有如期望的那樣,因為這是一個靜态數組,當N大于M的時候那麼就會趨向N了,複雜度就會回到連結清單的查找。是以可以考慮使用動态數組的方法進行擴充。也就是讓M産生變化,當N/M大于一定元素的時候就需要進行擴容,改變M了,當插入資料過少那麼久可以縮榮。
首先就是要實作一個resize方法了:
private void resize(int capacity){
TreeMap<K, V>[] newHashTable = new TreeMap[capacity];
for (int i = 0; i < capacity; i++) {
newHashTable[i] = new TreeMap<>();
}
int oldM = this.M;
this.M = capacity;
for (int i = 0; i < oldM; i++) {
TreeMap<K, V> treeMap = hashtable[i];
for (K key : treeMap.keySet()){
newHashTable[hash(key)].put(key, treeMap.get(key));
}
}
this.hashtable = newHashTable;
}
注意到M和新的M之間有一個陷阱,hash中用的是原來的M,而周遊的時候要周遊的是原來的M,是以應該要儲存一份。之後就隻需要在添加和移除兩個操作修改容量即可。
由于均攤複雜度是由
決定的,是以複雜度是在
。但事實上這樣擴容還有一個問題,乘上兩倍之後M就不是素數了,是以動态擴容的時候還需要選取素數的問題。
哈希表的均攤複雜度那麼久接近于
,很快,但是得到了什麼就會失去了什麼,這裡哈希表久犧牲了順序性,樹結構都是有順序性的,是以稍微慢一點。哈希表其實也是一個集合,有序集合可以用樹結構作為底層資料結構來實作,無序集合可以用哈希表來實作。
hash沖突——開放位址法
如果遇到了沖突,那麼就用線性探測的方法,加一看看有沒有空的,沒有繼續加一。但是這樣效率有時候是很低的,這裡就可以采用類似計算機網絡裡面的碰撞檢測方法,平方探測,一開始是1,又沖突了就4,9,16這樣既可。另外還可以使用二次哈希的方法。
最後附上所有GitHub代碼: https://github.com/GreenArrow2017/DataStructure_Java