二叉樹是資料結構中比較有意思的部分
二叉樹有兩種存儲形式
1: 線性表
2:指針
其實連結清單是很重要的,二叉樹就可以看為多條連結清單組合在一塊。在這裡主要是指針來實作的。 這裡基本的算法都用到了遞歸實作
那在二叉樹 中重要的算法如下:
a:建立一個二叉樹(采用前序,活着中序,活着後序)
b:周遊二叉樹(前序,中序,後序)
c:葉子結點的個數
d:樹的高度
e:度為一的節點數
f:度為二的節點數
g:有分枝的節點數
h:查找某個節點
可能剛開始不能了解遞歸,找一個二叉樹的圖像,根據程式走一遍就基本能了解。
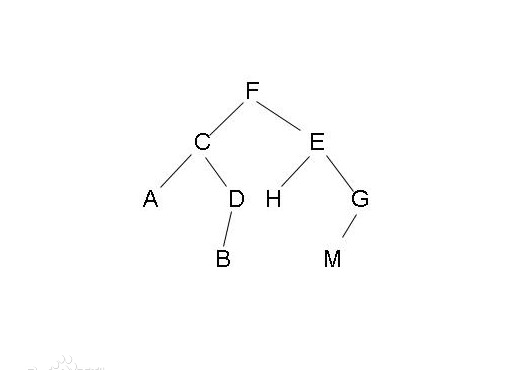
那這個二叉樹的前序周遊為。fcadbehgm
中序周遊為:acbdfehmg
後序周遊為:abdchmgef
//
// main.cpp
// 二叉樹,中序周遊
//
// Created by 劉小成 on 2018/10/20.
// Copyright © 2018 劉晨. All rights reserved.
//
include<iostream>
using namespace std;
typedef struct bitNode{
char data;
bitNode *lChild;
bitNode *rChild;
}bitNode;
class Tree{
private:
bitNode *head;
void creatBitNode(bitNode *& t);//建立一棵樹
void orderBitNode(bitNode *t);//中序周遊
void inorderBitNode(bitNode *t);//後序周遊
int countLeaf(bitNode *t);//葉子數量
int heightBitNodeTree(bitNode *t);//樹高
int oneBitNode(bitNode *t);//度為一 的節點
int twoBitNode(bitNode *t);//度為二的節點
int branchBitNode(bitNode *t);//有分枝的節點
public:
Tree(){head = NULL;}
void creatTree(){
bitNode *temp;
creatBitNode(temp);
head = temp;
}
void orderTree(){
bitNode *t = head;
cout<<"後序周遊的結果是: \t";
orderBitNode(t);
cout<<endl;
}
void inorderTree(){
bitNode *t = head;
cout<<"中序周遊的結果是: \t";
inorderBitNode(t);
cout<<endl;
}
void countLeafTree(){
bitNode *t = head;
cout<<"葉子節點的個數是:\t"<< countLeaf(t)<<endl;
}
void heightTree(){
bitNode *t = head;
cout<<"樹的高度是:\t"<< heightBitNodeTree(t)<<endl;
}
void oneBitNodeTree(){
bitNode *t = head;
cout<<"度為一的節點個數是:\t"<<oneBitNode(t)<<endl;
}
void twoBitNodeTree(){
bitNode *t = head;
cout<<"度為二的節點個數是:\t"<<twoBitNode(t)<<endl;
}
void branchTree(){
bitNode *t = head;
cout<<"有分枝的節點個數是:\t"<<branchBitNode(t)<<endl;
}
};
void Tree::creatBitNode(bitNode *&t){
char data;
cin>>data;
if(data == '.') t=NULL;
if(data != '.'){
t = new bitNode;
t->data = data;
creatBitNode(t->lChild);
creatBitNode(t->rChild);
}
}
void Tree::orderBitNode(bitNode *t){
if(t == NULL) return;
else {
orderBitNode(t->lChild);
orderBitNode(t->rChild);
cout<<t->data;
}
}
void Tree::inorderBitNode(bitNode *t){
if (t == NULL) return ;
if(t != NULL){
inorderBitNode(t->lChild);
cout<<t->data;
inorderBitNode(t->rChild);
}
}
int Tree::countLeaf(bitNode *t){
if(t == NULL) return 0;
else {
int m = countLeaf(t->lChild);
int n = countLeaf(t->rChild);
if( m+n == 0) return 1;
else return m+n;
}
}
int Tree::heightBitNodeTree(bitNode *t){
if(t == NULL) return 0;
else{
int m = 1+heightBitNodeTree(t->lChild);
int n = 1+heightBitNodeTree(t->rChild);
return m>n ? m:n;
}
}
int Tree::oneBitNode(bitNode *t){
if(t==NULL) return 0;
else {
if( (t->lChild !=NULL && t->rChild == NULL) || (t->lChild == NULL && t->rChild !=NULL) ){
int m = oneBitNode(t->lChild);
int n = oneBitNode(t->rChild);
return 1+m+n;
}
else{
int m = oneBitNode(t->lChild);
int n = oneBitNode(t->rChild);
return m+n;
}
}
}
int Tree::twoBitNode(bitNode *t){
if( t== NULL) return 0;
else{
if( t->lChild != NULL && t->rChild != NULL){
int m = twoBitNode(t->lChild);
int n = twoBitNode(t->rChild);
return 1+m+n;
}
else{
int m = twoBitNode(t->lChild);
int n = twoBitNode(t->rChild);
return m+n;
}
}
}
int Tree:: branchBitNode(bitNode *t){
if (t == NULL) return 0;
else{
if(t->lChild != NULL || t->rChild != NULL){
int m = branchBitNode(t->lChild);
int n = branchBitNode(t->rChild);
return 1+m+n;
}
else{
int m = branchBitNode(t->lChild);
int n = branchBitNode(t->rChild);
return m+n;
}
}
}
int main(int argc, const char * argv[]) {
cout<<"先序建立一棵樹\t\t 用"."表示NULL \n";
cout<<"輸入\n";
Tree a ;
a.creatTree();
a.inorderTree();
a.orderTree();
a.countLeafTree();
a.heightTree();
a.oneBitNodeTree();
a.twoBitNodeTree();
a.branchTree();
return 0;
} 在私有方法裡面建立遞歸函數,在公有函數裡面調用遞歸函數。這樣做的目的是不會産生多餘的變量,變量連接配接緊密。
在建立遞歸函數的時候要考慮好函數的出口,好讓函數可以傳回。然後就要考慮遞歸函數裡面遞歸的内容,将問題細小化。比如在統計葉子結點有多少個,
那函數的出口就是 這個節點是不是為空,若是空 ,就傳回,
函數的遞歸内容就是。 對一個節點來說,先統計一個它的左子樹的節點,在統計一下右子樹的節點, 如果兩邊都是0,那他就是葉子結點,那就葉子結點,傳回1,否則就不是葉子結點, 那就傳回這個樹的左邊葉子結點數+右邊的節點數。
那在對于樹的高度函數來講
image.png
在建立二叉樹的時候要規定一個輸入值,當這個值輸入的時候那他就NULL。在上面中 作者規定的是“.”,
二叉的這些算法中對于遞歸的要求比較高。
那對于二叉樹的度為一的節點的遞歸函數思想如下:
那度為二的節點其實和上面的思路是一樣的。還有有分枝的節點。