Morris周遊

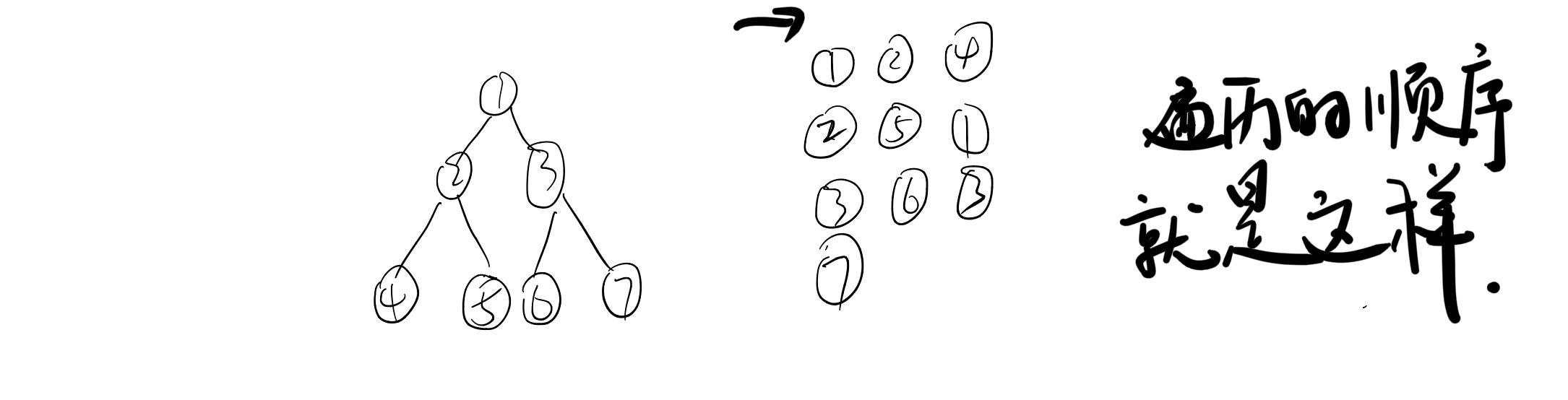
二叉樹遞歸周遊的實質是，隻要這個節點不為空，那麼這個節點一定會周遊3次，先序中序後續隻不過是列印的時機不同。先序是第一次到達這個節點，中序是第二次，後序是第三次。Morris周遊高度模仿這個過程。Morris周遊，如果這個節點有左子樹，那麼能到達這個節點兩次，沒有左子樹，隻能到達這個節點一次。Morris周遊的時間複雜度為O(n)，空間複雜度為O(1)。

morris.jpg

Morris周遊的規則如下

• 來到的目前節點記為cur（引用）， 如果cur無左孩子，cur向右移動，cur = cur.right。

• 如果cur有左孩子，找到cur左子樹最右的節點，記作mostRight

  1）如果mostRight的right指針指向空，讓其指向cur，cur向左移動

  （cur = cur.left）。

  2）如果mostRight的right指針指向cur，讓其指向空，cur向右移動。

然後，值得注意的是，Morris周遊可以寫成二叉樹的先中後，相關的方法會在代碼中注釋

public class MorrisTraversal {

    public static  class Node{
        public int value;
        public Node left;
        public Node right;

        public Node(int value){
            this.value = value;
        }
    }

    //morris周遊
    public void morris(Node head){
        if(head == null)
            return;
        Node cur = head;
        Node mostRight = null;
        while(cur != null){
            mostRight = cur.left;
            //左孩子不為空的情況
            if(mostRight != null){
                //找到最右的節點
                while(mostRight.right != null && mostRight.right != cur)
                    mostRight = mostRight.right;

                if(mostRight.right == null){
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                }else {
                    mostRight.right = null;
                }
            }
            System.out.print(cur.value + " ");
            cur = cur.right; //左孩子為空，直接向右移動
        }
        System.out.println();
    }

    //Morris前序周遊
    public void morrisPre(Node head){
        if(head == null)
            return;
        Node cur = head;
        Node mostRight = null;
        while(cur != null){
            mostRight = cur.left;
            //左孩子不為空的情況
            if(mostRight != null){
                //找到最右的節點
                while(mostRight.right != null && mostRight.right != cur)
                    mostRight = mostRight.right;

                if(mostRight.right == null){
                    mostRight.right = cur;
                    System.out.print(cur.value + " ");
                    cur = cur.left;
                    continue;
                }else {
                    mostRight.right = null;
                }
            }else {
                System.out.print(cur.value + " ");
            }
            
            cur = cur.right; //左孩子為空，直接向右移動
        }
        System.out.println();
    }


    
    //後面的太複雜了，暫時先放着。。。
    //Morris中序周遊


    //Morris後續周遊

    public static void main(String[] args) {
        Node head = new Node(4);
        head.left = new Node(2);
        head.right = new Node(6);
        head.left.left = new Node(1);
        head.left.right = new Node(3);
        head.right.left = new Node(5);
        head.right.right = new Node(7);
        new MorrisTraversal().morris(head);
    }
}