Motivation
《Time, Clocks, and the Ordering of Events in a Distributed System》大概是在分布式領域被引用的最多的一篇Paper了。
這篇Paper自己去年讀過兩次,最近嘗試翻譯了一下。第一是覺得太經典了,分布式領域必讀論文;第二是想再加深下自己的了解。
英文水準有限,有興趣還是建議讀一下原文。
Abstract
本文審視了在分布式系統中,一個事件發生在另一個事件之前(“happening before”)的概念,并用它描述了事件的偏序關系。 給出了一種分布式算法,該算法用于同步邏輯時鐘系統,邏輯時鐘系統可以用于确定事件的全序關系。 全序關系的用途被作為一種解決同步問題的方法給出。 這個方法之後被專門用于解決同步實體時鐘,并且限定同步時鐘的誤差。
Introduction
在我們的思維中,時間是一個非常基礎的概念。它來源于更基礎的概念——時間的發生順序。我們說事件發生在3:15,假如時鐘已經走到3:15但是每到3:16。事件的時間順序的概念貫穿于我們對系統的思考。比如,在航空預定系統中,如果預定操作在航班滿員之前,那麼預定操作需要被允許。但是,在分布式系統中,我們需要仔細的重新審視這個概念。
分布式系統由一系列空間上分離,通過交換資訊來通信的程序組成。一個換聯網的計算機網絡,如ARPA,是一個分布式系統。單台計算機也可以被看做是由中心控制單元,記憶體單元,輸入輸出等不同的程序組成的分布式系統。如果與單個程序内事件發生的間隔時間相比,系統中消息的傳遞延遲不可以被忽略,那麼這個系統可以被認為是一個分布式系統。
我們主要關注空間上分離的計算機。但是我們的很多結論能被廣泛的應用。特别是因為不可預知的事件發生順序,單個計算機上的多處理系統涉及的問題和分布式系統的問題非常相似。
在一個分布式系統中,有時候無法确定一個事件發生于另一個事件之前。而“發生之前”的關系隻是系統中事件的一個偏序關系。我們發現由于人們沒有弄清楚這一點而導緻一些問題問題的出現。
在這篇論文中,我們讨論偏序關系,并給出一個分布式算法将其拓展為所有事件的全序關系。這個算法能夠提供有效的機制來實作一個分布式系統。我們通過一個解決同步問題的簡單方法來說明它的用法。不幸的是,如果通過這個算法得出的順序和用于感覺的不一樣,可能會發生異常的行為。這可以通過引入真實的實體時鐘來避免。我們描述了同于同步這些時鐘的簡單方法,并且推導出了時鐘偏差的範圍。
The Partial Ordering
大部分人會認為事件a發生于事件b之前,如果事件a發生的時間早于事件b。他們可能通過實體理論事件來證明這個定義。但是,如果一個系統需要正确的符合規範,那麼必須根據系統中可觀察的時間給出該規範。假如規範是在實體時間的條款下給出的,那麼系統中必須包含一個真實的時鐘。即使真的包含實體時鐘,依舊會存在問題,因為時鐘會存在誤差。是以我們将不通過實體時鐘來定義“事件a發生于事件b之前”。換言之,單個程序中的事件是有預先的順序關系的。這看起來符合單程序的實際情況。當然,我們可以對我們的定義進行拓展,進而将當個程序劃分為多個子程序,但我們沒有必要這麼做。
我們假設發送和接收一條消息時一個程序中的一個事件。我們将“a發生于b之前”的關系定義為a→b,即→表示“發生于...之前”。
定義→關系需要滿足一下三個條件:(1)如果事件a、b在一個程序中,a發生于b之前,那麼a→b;(2)如果a是發送一條消息的事件,而b是接收這條消息的事件,那麼a→b;(3)假如a→b成立,且b→c成立,那麼a→c成立。如果兩個事件a、b不滿足a→b或者b→a,那麼認為a、b兩個事件是并發的。
我們假設a→a是不成立的(一個事件發生于自己之前顯得沒有什麼意義),那麼→是不具備自反性的偏序關系。
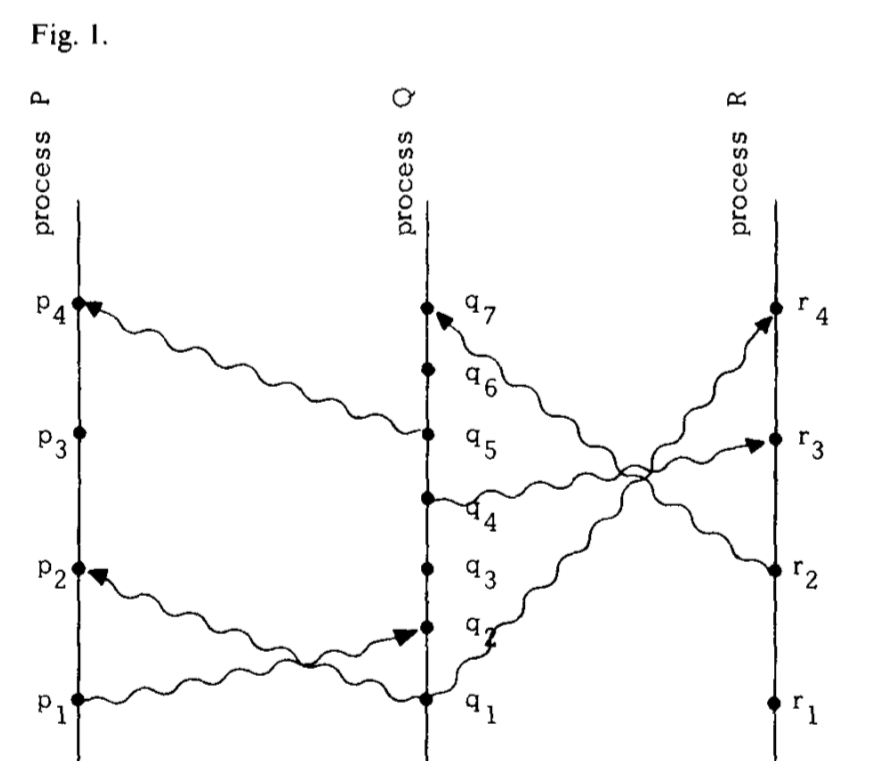
通過圖1這樣的“時空圖”對了解這個定義是非常有幫助的。水準方向表示空間,垂直方向表示時間——越遲的時間在垂直方向上的位置更高。點表示事件,垂直線表示程序,波浪線表示消息。顯而易見的,a→b意味着可以沿着程序線和消息線從a點到達b點。比如圖一中的p1→r4(p1→q2→q4→r3→r4)。
也可以換一種方式來了解該定義,比如可以認為a->b意味着是事件a導緻了事件b的發生。如果兩個事件互相之間沒有因果關系,我們就認為它們是并行發生的。比如圖1中的p3和q3就是concurrent的。盡管圖畫地讓人覺得q3比p3發生的實體時間要早,但是程序P在p4那一點收到消息之前是根本不知道程序Q何時執行了q3的。(在事件p4之前,P程序最多能知道計劃要在q3做的事情)。
這個定義對于那些熟悉狹義相對論時空觀的人應該會顯得比較自然。在相對論中,事件間的順序是通過可能被消息來定義的。但是,我們采用了更實用的方法,隻考慮那些實際中真的被發送的消息。當然如果知道了那些實際發生的事件,我們就可以判斷系統是否工作正常,而不需要知道那些可能會發生的事件。
Logical Clocks
現在我們将邏輯時鐘引入到系統中。我們将邏輯時鐘抽象成隻是給事件配置設定編号,編号代表事件發生的時間。更準确的說,我們為程序Pi定義一個時鐘Ci為程序中的每個事件配置設定一個編号Ci<a>。系統的全局時鐘為C,對任意事件b,它的時間為C<b>,如果b是程序j中的事件,那麼C<b>=Cj<b>。目前為止,對Ci我們沒有引入任何實體時鐘的依賴,是以我們可以認為Ci是邏輯上的時鐘,和實體時鐘無關。它可以采用計數器的方式實作而不需要任何計時機制。
我們現在來考慮對于這樣一個時鐘系統的正确性的涵義。我們不能将定義的正确性基于實體時間之上,因為這需要引入持有實體時間的時鐘。我們的定義必須基于事件發生的順序。合理的條件是,如果事件a發生在另一個事件b之前,那麼a發生的時間應該早于b。将該條件更形式化地表述如下:
*Clock Condition.* For any event a and b:
if a → b then C<a> < C<b>
需要注意的是我們不能期望這個條件的逆命題成立,即C<a> < C<b>并不意味着a → b。因為如果相反的條件也成立,那麼意味着并發的事件必須發生在同一時間(命題和逆命題都成立的條件下,并發就隻能是C<a>=C<b>)。比如圖1中,p2、p3都和q3并行,如果逆命題成立,那麼p2、p3發生在同一時間,這和實際p2→p3的關系沖突。
從我們隊“→”關系的定義可以看出,如果滿足一下兩個條件,那麼久滿足Clock Condition:
- 如果a、b是同一個程序中的事件,且a發生在b之前,那麼C<a> < C<b>
- 如果a、b是不同程序中的事件,且a是發送一條消息的事件,而b是接收這條消息的事件,那麼C<a> < C<b>
從時空圖的角度考慮時鐘。我們假設程序的時鐘在每個事件之間tick,且每次tick增加1。比如a、b是Pi程序中的事件,如果Ci<a> = 4,C1<b> = 7,那麼這兩個事件之間時鐘會走過5、6、7。如果我們通過虛線(時間線)将所有tick的點連接配接起來,那麼圖1看起來會類似圖2。Condition C1意味着同一個程序中任何兩個事件之間都有一條虛線;Condition C2意味着消息線必然和虛線交叉。
我們可以将時間線作為空間時間上一些笛卡爾坐标系的時間坐标線。我們可以将圖2中的時間線拉直,那麼可以得到圖3。圖3是對圖2的另一種更好了解的描述。在沒有引入實體時間的情況下,沒有辦法判斷這3幅圖哪一幅圖更好的表示了系統的狀态。
讀者會發現如果将程序想象成一個二維的網絡圖,那麼将産生一個三維的時空圖。程序和消息仍然由線表示,時間線則變成了一個二維的平面。
現在讓我們假設這些程序是一些算法,事件表示算法執行過程中的一些行為。我們将如何進入滿足Clock Condition的時鐘。程序Pi的時鐘由Ci表示,Ci<a>表示Pi中a發生的時間,Ci的值在發生事件時會改變,Ci的改變本身不包含事件。
為了滿足Clock Condition,我們需要確定滿足C1、C2條件。C1非常簡單,程序隻需要按照以下步驟:
IR1:任何一個程序Pi在兩個成功事件之間遞增Ci
為了滿足C2,我們需要每條消息m包含一個時間戳Tm,Tm表示消息被發送的時間。收到該消息的程序需要将時鐘調整到大于Tm。更準确的,需要滿足一下規則:
IR2:(a) 如果事件a表示Pi程序發送消息m,那麼m包含一個時間戳Tm,Tm=Ci<a>。(b)程序Pj收到消息m,Pj需要将Cj設定為等于或大于目前值,且大于Tm的值。
在IR2中,我們認為代表消息m被接收的時間在設定Cj之後(其實含義是需要将時間進行調整,之後再處理這條消息)。很明顯,IR2保證了條件C2的滿足。是以,IR1和IR2保證了Clock Condition的滿足,這樣它們就保證了得到的是一個正确的邏輯時鐘系統。
Ordering the Events Totally
我們可以使用滿足Clock Condition的時鐘系統來擷取系統中所有事件的全序關系。我們簡單的将他們按照發生的時間進行排序。為了打破僵局,我們使用系統的任意一個全序關系:“<”。更精确的,我們定義一個關系"=>":對于Pi中的事件a和Pj中的事件b,如果C<a> < C<\b>或C<a> = C<\b>,且Pi < Pj,那麼a=>b。顯而易見的,這是一個全序關系,同時如果a->b,那麼a=>b。換言之,=>将“發生于...之前”的偏序關系變成了全序關系。
=>的順序關系依賴于系統的時鐘Ci,并且不是唯一的。選擇滿足Clock Condition的不同系統時鐘将得到不同的全序關系。對于給定的全序關系,一定會有一個滿足Clock Condition的系統時鐘。隻有偏序關系是由系統的事件唯一決定的。
能确定事件的全序關系對實作分布式系統是非常有用的。實際上,實作一個系統邏輯時鐘的目的就是為了獲得全序關系。我們将通過解決版本互斥的問題來說明全序關系的使用。考慮一個由多個程序組成,且貢獻一個資源的系統。一個時刻隻能有一個線程使用資源,是以線程間需要同步來避免沖突。我們希望尋找一個滿足如下三個條件的算法來将資源配置設定給線程:1. 資源在配置設定給其他程序前,需要擷取了資源的程序進行釋放資源的操作;2. 資源的請求必須按照請求的發生順序進行配置設定;3. 如果每個被授予資源的程序最終都釋放了資源,那麼每個請求最終都會被授予資源。
我們假設初始狀态資源隻會被配置設定給一個程序。
這些事非常自然的需求。他們準确的定義了什麼樣的解決方案是正确的。觀察這些條件是如何涉及到事件順序的。對于條件2,它并沒指定對于并發請求的授權順序。
認識到這是一個不平凡的問題非常重要。采用中心程序來統一授權的方式并不能解決這個問題,除非添加額外的假設。來看這樣的場景,P0為中心授權的程序;如果P1像P0發起申請資源的請求,之後給P2程序發送消息;P2程序收到後也想P0程序申請資源;P2的請求可能先于P1的請求到達P0,那麼條件2将被違反(沒有按照請求發生的時間來授權)。
為了解決這個問題,我們實作了一個滿足IR1和IR2的系統時鐘,然後用它來定義一個全序關系=>。這提供了所有request和release操作的順序。利用這個順序就可以比較容易的找到一個解。它隻需要確定每個程序知道其他程序的操作。
為了簡化問題,我們做了一些假設。這些假設不是必須的,但是引入他們可以避免陷入細節的讨論當中。首先,我們假設所有任何兩個程序Pi和Pj,所有從Pi發送到Pj的消息都将按照他們的發送順序被Pj接收。其次,我們假設所有的消息都會被接收(這些假設可以避免引入消息序号和确認機制)。最後,我們假設一個程序能直接的向所有的其他程序發送消息。
每個程序會維護一個它自己的,對其他程序不可見的請求隊列。我們假設請求隊列初始狀态隻有一個消息T0:P0資源請求,P0代表初始時刻獲得資源授權的程序,T0小于任意時鐘初始值。
算法由以下5個規則定義。友善起見,假設每個規則定義的行為為一個獨立的事件。
- 為了申請資源,Pi發送資源申請請求Tm:Pi給所有其他的程序,并将消息放入自己的請求隊列。Tm表示消息的時間。
- 當Pj收到Tm:pi的請求,将其放入請求隊列并發送一個帶有時間戳的ACK給Pi。
- 釋放資源時,Pi将Tm:Pi從請求隊列中移除,并發送一個帶有時間戳的Pi釋放資源的消息給所有的其他程序。
- 當Pj接收到Pi釋放資源的消息時,它将Tm:Pj請求資源的消息從請求隊列中移除。
- 當以下兩個條件被滿足時Pi獲得資源:(a)按=>的順序,Tm:Pi的消息在請求隊列的最前面;(b)Pi從其他每個程序至少收到了一條時間戳大于Tm的消息。
條件5中的(a)、(b)都隻需要在Pi本地進行驗證。
很容易驗證滿足以上規則的算法滿足之前的資源配置設定算法的1、2、3條件(1. 資源在配置設定給其他程序前,需要擷取了資源的程序進行釋放資源的操作;2. 資源的請求必須按照請求的發生順序進行配置設定;3. 如果每個被授予資源的程序最終都釋放了資源,那麼每個請求最終都會被授予資源)。首先觀察規則5的條件b,假設消息是順序接收的,就可以保證Pi已經收到了所有排在它目前請求之前的所有請求。隻有規則3和規則4會從請求隊列中删除消息,是以可以很容易的看出條件1是滿足的。條件2可以通過如下事實得出:全序關系=>是對偏序關系->的拓展。規則2保證了在Pi發出資源請求後,規則5的條件(b)最終一定會成立。規則3和4意味着如果擷取了資源授權的所有程序最終釋放掉資源後,那麼規則5的條件(a)最終也一定會成立,這就證明了條件(3)。
這是一個分布式算法。每個獨立的程序遵循這些規則,算法中沒有中心同步程序,也沒有中心儲存設備。該方法可以被通用化,來實作分布式的多程序系統所需要的任意同步機制。同步過程可以通過狀态機來描述,該狀态機包含一個指令集合C,一個可能的狀态集合S,以及一個函數e:C×S->S。關系e(C,S)=S’的含義是,在處于狀态S的狀态機執行指令C,将會使狀态機轉移到狀态S’。在我們的例子中,C包括所有的Pi資源請求和資源釋放指令,狀态包括一個處于等待狀态的請求指令隊列,同時處于隊列頂端的那個請求就是要被授權的那個。請求指令的執行将會将該請求添加到隊列末尾,釋放指令的執行将會從隊列中删除一個指令。
每個程序獨立地通過使用所有程序産生的指令來驅動該狀态機的執行。所有的程序按照指令的時間戳激進行排序,是以所有的程序都會使用相同的指令序列。當一個程序收到所有的其他程序發出的小于或者等于T的指令之後他就能執行T的指令。具體的算法已經很明了了,是以我們不再進行描述。
該方法使得我們可以在分布式系統中實作多程序的同步。但是,該算法要求所有程序都參與其中。每個程序需要知道所有其他程序的所有指令,是以單個程序的故障将使其他程序的狀态機無法正确變更,進而導緻系統停止工作。
錯誤處理是一個很困難的問題,同時對它進行細節性的讨論已經超出了本篇文章的範圍。隻是需要指出的是,failure這個概念隻有在實體時間上下文中才有意義。如果沒有實體時間,就沒有辦法去區分程序是出錯了還是隻是處于事件之間的間歇。使用者隻能通過系統很長時間都沒有響應來判斷系統出了問題。在程序或通信線路出錯時也能正常工作的方法,我們将會在[3]中進行描述。(Lamport, L. The implementation of reliable distributed multiprocess systems. To appear in Computer Networks.)
Anomalous Behavior
我們的資源排程算法按照全序關系對請求進行排序。這允許下面這種異常行為的發生。考慮一個由互相連接配接的計算機組成的全國性系統。假設某人在計算機A上産生了一個請求A,然後他打電話告訴住在另一個城市裡的朋友B,讓它在計算機B上産生一個請求B。對于請求B來說很有可能會獲得一個更小的時間戳然後被排在A前面。這是有可能發生的,因為系統沒有辦法知道A實際上發生在B之前,因為該資訊是基于位于系統外部的消息的。
讓我們更深入地考察下該問題産生的根源。令∮代表所有系統事件組成的集合,然後我們再引入一個包含了∮中的事件以及所有其他外部事件(比如上面例子中的打電話)的集合∮’。令->(注意這個是加粗的->,與前面的->不同)表示∮’中的happen before關系。在上面的例子中,有A->B,但是A!->B。很明顯一個完全基于∮中的事件,而對的∮’中的其他事件沒有任何聯系的算法,是無法保證請求A會被排在請求B前面的。
有兩種可能的方式可以避免這種異常行為。第一種方式是将關于->順序的必要資訊顯式地引入到系統中。比如在上面的例子中,該使用者在産生請求A時可以擷取它在系統中的時間戳T,然後他可以在打電話通知他朋友的時候,告訴他這個時間戳,然後在他朋友産生請求B的時候,告知系統産生一個晚于T的時間戳。這樣就将這種異常行為交給使用者自己來負責。
第二種方法就是構造一個滿足如下條件的時鐘系統:
Strong Clock Condition.對于∮’中的任意兩個事件,如果a->b,那麼C<a> < C<b>。
該條件要比之前的Clock Condition強,因為->比->要強。通常我們的邏輯時鐘無法滿足該條件。
如果我們令∮’表示實體時空中真實事件的集合,令->代表由狹義相對論所定義的事件偏序關系。在我們所在的宇宙中,是有可能構造出一個由互相之間獨立運作的多個實體時鐘構成的滿足Strong Clock Condition的時鐘系統的。是以我們可以使用實體時鐘來避免這種異常行為。下面我們就将注意力轉移到這類時鐘之上。
Physical Clocks
現在我們将實體時間引入到我們的時空圖中,令Ci(t)表示在實體時間t所讀取到的時鐘Ci的值。為了友善數學表述,我們假設時鐘是以連續而非離散的滴答走動的。更準确地說,我們假設Ci(t)是一個在時間t上的連續的可微分函數,除了那些時鐘被重置時的孤立突變點之外。dCi(t)/dt代表了時鐘在時間t時的速率。
如果将時鐘Ci作為一個真實的實體時鐘,那麼它還必須以一個近似正确的速率來運作。也就是說,必須要保對于所有的t,dCi(t)/dt≈1。更準确地說,我們要保證滿足如下條件:
PC1.存在一個常數k,對于所有的i:| dCi(t)/dt -1|<k
對于典型的由晶體控制的時鐘來說,k<=10^-6.
如果時鐘隻是單單地以近似正确的速率運作是不夠的。它們還必須是同步的,即對于所有的i,j,t來說,Ci(t)≈Cj(t)。更準确地說,必須存在一個足夠小的常數e,滿足如下條件:
PC2.對于所有的i,j:| Ci(t)-Cj(t)|<e.
如果我們讓圖2中的垂直距離來表示實體時間的話,那麼PC2意味着單個滴答線上的高度差異要小于e。
由于兩個不同的時鐘永遠都不會以相同的速率走動,這意味着它們之間的偏差會越來越大。但是,首先我們來看一下k和e要多小才能避免異常行為。我們必須要保證系統∮’中的所有相關事件都滿足Strong Clock Condition。首先我們假設我們的時鐘滿足普通的Clock Condition,那麼隻需要保證∮’中那些不滿足a->b的事件滿足Strong Clock Condition。是以我們隻需要考慮發生在不同程序中的事件。
令u表示滿足如下條件的值:如果事件a發生在實體時間t,同時b是發生在另一個程序中的滿足a->b事件,那麼b肯定發生在實體時間t+u之後。換句話說,u需要小于程序間消息傳輸的最短時間。我們可以用程序間的距離除以光速的值作為u的值。當然,這取決于∮’中消息是如何傳輸的,u的值也可以很大。
為避免異常行為,我們必須保證對于任意i,j,t:Ci(t+u)-Cj(t)>0,再結合PC1和PC2,我們就可以建立起所需要的最小的k和e值與u之間的關系。同時我們假設時鐘被重置時,它的時間隻會超前而絕不會後退(後退會導緻條件C1被違反)。PC1意味着Ci(t+u)-Ci(t)>(1-k)u。再結合PC2,就可以很容易地得出如果如下不等式成立,那麼Ci(t+u)-Cj(t)>0就成立:e(1-k) <= u。該不等式再加上PC1和PC2就可以保證異常行為不會發生。
現在我們來描述下用來保證PC2成立的算法。令m表示一個在實體時間t發送和時間t’被接收的消息。我們定義Vm=t’-t來表示消息m的總延遲。當然,接收消息m的程序并不知道該延遲。但是我們假設接收程序知道某個最小延遲取值Um>=0,并且Um<=Vm。我們稱Em=Vm-Um為消息的不可預測的延遲部分。
現在我們将規則IR1和IR2針對實體時鐘修改如下:
IR1’.對于每個i,如果Pi在實體時間t未收到消息,那麼Ci是在時間t就是可微分的并且dCi(t)/dt>0.
IR2’.(a)如果Pi在實體時間t發送了一個消息m,那麼m将包含一個時間戳Tm=Ci(t).(b)當在時間t’接收到消息m時,程序Pj将設定Cj(t’)等于max(Cj(t’-0),Tm+Um).(注:Cj(t’-0)=[limCj(t’-|&|),&->0])
盡管這些規則的描述使用的都是實體時間,程序隻需要知道它自己的時鐘值以及它接收到的消息中的時間戳即可。為了數學描述的友善,我們假設事件均發生在一個精确的實體時間點上,同時相同程序的不同僚件發生在不同的時間。這些規則僅僅是針對規則IR1和IR2的一個特化版本,是以我們的時鐘系統是滿足Clock Condition的。實際上,由于真實的事件都會持續一段有限的時間,這就使得該算法實作起來沒有什麼困難。實作唯一需要注意的是要確定離散的時鐘滴答是足夠頻繁的,可以保證滿足C1。
現在我們來展示一下如何用該時鐘同步算法來保證條件PC2的滿足。我們假設該系統可以用一個有向圖來表示,圖中從程序Pi到程序Pj的邊表示一個通信線路,消息可以直接通過該線路從Pi發送到Pj。同時我們假設每τ秒就會有一條消息通過該線路,這樣對于任意的時間t,在實體時間t到t+τ之間,Pi至少發送了一條消息到Pj。有向圖的直徑是滿足如下條件的最小值d:對于任意的兩個程序Pj,Pk,都存在一條從Pj到Pk的路徑,該路徑最多具有d條邊。
除了建立起了PC2,下面的定理還給出了系統首次啟動時令時鐘達到同步狀态所花時間的上界。
THEOREM假設一個半徑為d的由多個程序組成的強連通圖始終滿足規則IR1’和IR2’。同時對于任意消息m,Um<=某常數U,以及任意時刻t>=t0來說:(a)PC1成立.(b)存在常數τ和ε,每τ秒都會有一個消息在不可預測的延遲部分小于ε的情況下在每條邊上傳送。那麼PC2就能被滿足,同時對于所有的t>t0+τd,e≈d(2kτ+ε),這裡我們假設U+ε<<τ。
該定理的證明令人吃驚地困難,詳細證明過程見附錄。目前針對實體時鐘的同步問題人們已經進行了大量的研究。推薦讀者閱讀[4]了解下這個問題(Ellingson, C, and Kulpinski, R.J. Dissemination of system-time. 1EEE Trans. Comm. Com-23, 5 (May 1973), 605-624.)。該領域提出的很多方法,都可以用來估計消息傳輸Um以及調整時鐘頻率dCi/dt(适用于那些允許進行調整的時鐘)。但是,看起來時鐘不能回退的這個要求使得我們的場景與之前被研究的那些有所不同,同時我們相信該定理是一個全新的結論。
Conclusion
可以看到“happening before”定義了分布式系統中事件的一個偏序關系。我們描述了一個可以将偏序關系拓展為某個全序關系的算法,同時展示了這個算法如何去解決簡單的同步問題。我們将會在未來的一篇paper裡展示如何對這種方法進行擴充以用來解決任意的同步問題。
該算法定義的全序關系有些随意。當系統與使用者觀察到的順序不一緻時會産生異常行為。該問題可以通過使用一個被正确同步的實體時鐘系統來避免。我們的定理還展示了時鐘可以被同步到怎樣的程度。
在分布式系統中,認識到事件的發生順序是隻是一個偏序關系是非常重要的。我們認為這個觀點對了解所有多程序的系統非常有幫助。它可以幫助人們了解多程序系統中的基本問題,撇開那些用于解決這些問題的各種機制。
如果本文對您有幫助,點一下右下角的“推薦”