決策樹的算法可謂是貼近我們的生活,通過下面的案例,你就會發現我們每天都在有意無意的使用着決策樹算法(好厲害的樣子)。
小明同學每天早上都要去學校,可步行、乘公交和坐隔壁老王叔叔的車(皮一下很開心)。這時,小明就開始做決策了:首先看天氣,不下雨時就選擇步行去學校;下雨時就看隔壁老王叔叔是否有空,有空就乘老王的車去學校,沒空就選擇乘公交去學校。如圖所示。
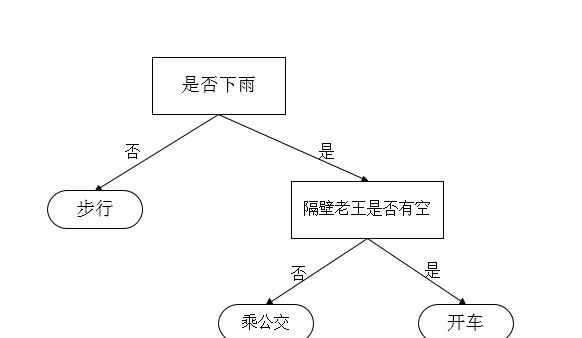
決策樹定義
通過上述案例,就可以對決策樹下定義了:上圖就是決策樹(嗯。。。有點敷衍)。決策樹由結點和有向邊組成。結點有兩種類型:内部節點和葉節點,内部節點表示一個特征或屬性(天氣,是否有空),葉節點表示一個類(步行、乘公交和坐隔壁老王叔叔的車)。
決策樹算法原理
那怎麼通過決策樹算法來構造這棵樹呢?(難道是上帝之手麼?)上述案例較簡單,我們現在提出一個很經典的案例,如圖所示,我們首先到底是通過天氣、濕度還是風級來進行決策了?這裡就要提出熵和資訊增益。
熵
首先,我們看什麼是熵。簡單來說,熵是描述事物的混亂程度的(也可以說是不确定性)。例如:中國足球進入世界杯,這個不确定性可能是0,是以熵可能就是0;6面的色子的不确定性比12面色子的要低,是以熵也會比其低。現在就來看熵的公式:H = -∑ni=1p(xi)log2p(xi)
那6面色子的熵:1/6*log21/6的6倍,也就是2.585
以此類推,那12面的熵就是:3.585
最後,我們計算下該案例的資訊熵:不打球為5,打球為9,是以熵計算為:
-(5/14 * log(5/14,2) + 9/14 * log(9/14,2))
0.940
資訊增益
到底先按哪個特征劃分資料集呢?我們有個原則,就是将無序的資料變得有序,換句話說,就是讓熵變小,變的越小越好。而資訊增益就是劃分資料集前後熵的變化,這裡就是要讓資訊增益越大越好。
我們以天氣為例,計算劃分後的資訊增益:
- 晴天時:2/5打球,3/5不打球,熵為:
-(2/5 * log(2/5,2) + 3/5 * log(3/5,2))
0.971
- 陰天熵:0
- 雨天熵:0.971
機器學習實戰之決策樹 天氣
天氣為晴天、陰天和雨天的機率為5/14,4/14和5/14,是以劃分後的熵為:5/14 * 0.971+4/14 * 0+5/14 * 0.971得0.693,資訊增益為0.940-0.693為0.247,同理可以求出其他特征的資訊增益。
這裡的天氣資訊增益最大,是以選擇其為初始的劃分依據。
選擇完天氣做為第一個劃分依據後,能夠正确分類的就結束劃分,不能夠正确分類的就繼續算其餘特征的資訊增益,繼續前面的操作,結果如圖所示。
結果機器學習實戰之決策樹
僞代碼
是以決策樹是一個遞歸算法,僞代碼如下:
def createBranch():
檢測資料集中的所有資料的分類标簽是否相同:
If so return 類标簽
Else:
尋找劃分資料集的最好特征(劃分之後資訊熵最小,也就是資訊增益最大的特征)
劃分資料集
建立分支節點
for 每個劃分的子集
調用函數 createBranch (建立分支的函數)并增加傳回結果到分支節點中
return 分支節點
決策樹之海洋生物分類
問題描述與資料
資料為判斷是否為魚類,有兩個特征:
- 在水中是否生存
- 是否有腳蹼 這裡需要我們自己手動構造資料:
機器學習實戰之決策樹
def creatDataSet():
dataSet = [
[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']
]
labels = ['no surfacing', 'flippers']
return dataSet, labels
這裡的dataSet為資料,labels是兩個特征的名稱。
計算熵
這裡我們定義一個計算資料集熵的函數:
from math import log
def calcshannon(dataSet):
num = len(dataSet)
labelCounts = {}
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannon = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/num
shannon -= prob * log(prob, 2)
return shannon
這個代碼比較簡單,就是對傳入的資料,以最後一列(也就是分類label)求熵。
劃分資料集
首先設定一個劃分資料集的函數,參數為:待劃分的資料,劃分的特征和傳回的特征值,該函數會在choose函數中被調用,用于計算最好的劃分特征。
def splitDataSet(dataSet, axis, value):
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value:
reduce = featVec[:axis]
reduce.extend(featVec[axis+1:])
retDataSet.append(reduce)
return retDataSet
def choose(dataSet):
numfeature = len(dataSet[0]) - 1
baseEntropy = calcshannon(dataSet)
bestinfogain = 0.0
bestfeature = -1
for i in range(numfeature):
featlist = [example[i] for example in dataSet]
vals = set(featlist)
newEntropy = 0.0
for value in vals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob*calcshannon(subDataSet)
infoGain = baseEntropy - newEntropy
if (infoGain > bestinfogain):
bestinfogain = infoGain
bestfeature = i
return bestfeature
建立樹
在所有特征使用完時,也沒法對資料進行徹底的劃分時,就需要使用多數表決來确定葉子節點的分類,代碼如下,類似前文中KNN中的排序。
import operator
def majority(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
sortedcount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedcount[0][0]
最後就是建立樹的代碼:
def createTree(dataSet, labels):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList):
return classList[0]
if len(dataSet[0]) == 1:
return majority(classList)
bestFeat = choose(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
del (labels[bestFeat])
Vals = [example[bestFeat] for example in dataSet]
uvals = set(Vals)
for value in uvals:
sublabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), sublabels)
return myTree
這裡有兩個終止遞歸的條件:一是所有類别能正确的劃分了,二是特征使用完成。
算法優缺點
- 優點:利于了解
- 缺點:容易過拟合