Hello 大家好,今天給大家帶來一份關于定位的概述入門性質的文章,看完這篇文章,你将了解Location的意義,以及一個最基本1D直方圖濾波的Demo,如果你隻是需要源代碼,請直接往下翻!
一、Location的意義
在機器人導航任務中,location 可以告訴機器人目前位置,以友善閉環控制或者軌迹規劃。一般情況下,Location 可以通過
GPS,WIFI 等方式完成。GPS的定位精度在3.5米左右,WIFI則大于10米。對于機器人、無人汽車而言,這樣的精度顯然是不可接受的。雷射雷達在10m的距離可以達到cm的精度,雙目視覺在4m可以達到10cm的精度,與GPS相比有一定優勢,此外,這種非線上的定位方式可以在室内使用。
Location 最大的難度來自于測量誤差。裡程計的計數誤差,測量與裡程計的不統一等。是以我們需要一種算法,能夠較高精度的确定機器人的位姿。
image
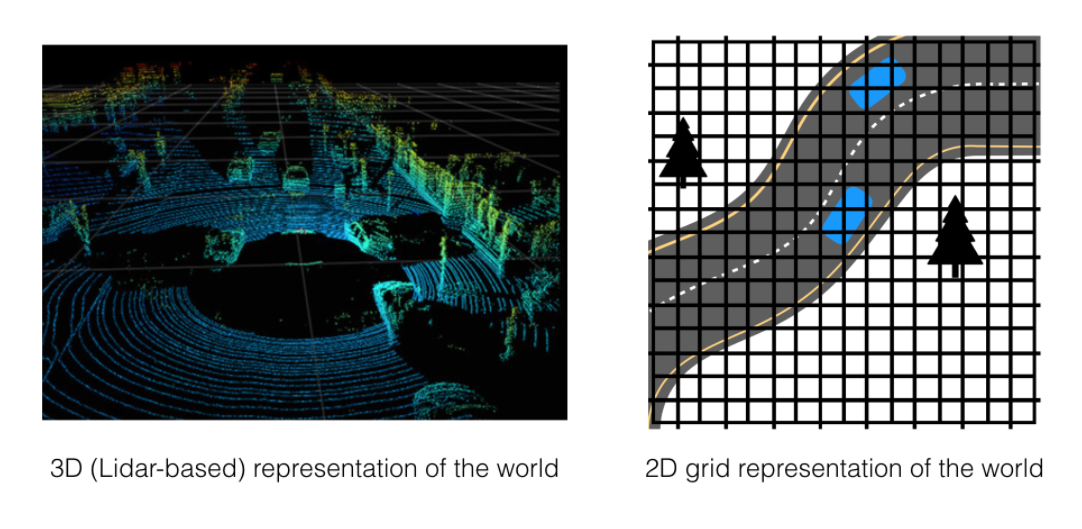
如上圖所示,那些環境的網格是一個個離散的單元,将連續的環境離散化,面對的是一個離散的機率分布,這樣子就意味着機器人可能處于的位置總數是有限的。下面我們将執行個體講解一個最基本的基于一維空間的網格Location的直方圖濾波算法,以初步定性的了解機器人Location算法。
下面的列子Udacity上的課程 https://cn.udacity.com/course/artificial-intelligence-for-robotics –cs373/
二、直方圖濾波
定義一個一維的網格空間
首先我們定義一個一維的網格空間,如下圖所示, 機器人就在這裡糾結自己處于哪一個格子;
初始化機率分布
接着我們需要初始化相應的機率分布:
初始機率
p=[0.2, 0.2, 0.2, 0.2, 0.2]
world=['green', 'red', 'red', 'green', 'green']
我們首先初始化沒一個網格的機率都占
0.2
的均勻分布,定義每一個網格的顔色,這樣子這個一維的網格地圖就初始化完畢了。
接着我們需要加入傳感器的資訊,以及機器人運動機率資訊。
加入傳感器與運動
measurements = ['red', 'red']
motions = [1,1]
pHit = 0.6
pMiss = 0.2
pExact = 0.8
pOvershoot = 0.1
pUndershoot = 0.1
在機器人運動過程中,我們首先定義機器人的運動模式
motions
分别是 -1 和 1,即移動方向左(-)右(+),假定格子是循環的(首尾聯通);
接着我們定義
pHit
和
pMiss
,他們分别代表的是實際值與測量值相同的機率和不同的機率,這個怎麼了解喃,我們來看一下下面這張圖:
如圖所示,機器人測量到的資訊是
red
, 真實的顔色分别是
['green', 'red', 'red', 'green', 'green']
,那麼機器人處于各個位置的機率就應該這樣計算,首先如果處于第一個網格,那麼表示機器人檢測錯了,則處于一個網格的值應該為:
0.2 * 0.2 = 0.04
,那麼同理可得,若處于第二個網格,就表明檢測對了,則相應的網格值為:
0.6 * 0.2 = 0.12
。
最終得到下面的數值分布:
['0.04', '0.12', '0.12', '0.04', '0.04', '0.04']
;
注意,這裡還不是機率分布,因為和不等于1,我們需要進行歸一化處理,需要知道具體的代碼實作請繼續往下看。
然後,我們定義了機器人自己運動正确到達每個位置的機率, 即使我們已經可以預測他到達的位置,但是實際運動總是存在誤差,可能是輪子打滑,遇到障礙物,中途沒電,等等,是以我們有不足/超調的三種情況:
- pExact = 0.8
- pOvershoot = 0.1
- pUndershoot = 0.1
就這樣我們定義了所有的機率分布,接着讓我們實作具體的算法吧。
算法主體包含兩個部分,測量值的更新和運動更新,最終得到各個網格的機率分布。
測量值更新
# update measurement
def sense(p, Z):
q=[]
for i in range(len(p)):
hit = (Z == world[i])
q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
s = sum(q)
# Normalized Sense
for i in range(len(q)):
q[i] = q[i] / s
return q
我們首先需要擷取所有的測量值:
for i in range(len(p)):
,之後分别與實際的
world[i]
比較,之後乘上相應的
pHit / pMiss
之後通過
sum
函數擷取總和用于皈依化處理,得到測量的機率分布。
運動更新
def move(p, U):
q = []
for i in range(len(p)):
s = pExact * p[(i-U) % len(p)]
s = s + pOvershoot * p[(i-U-1) % len(p)]
s = s + pUndershoot * p[(i-U+1) % len(p)]
q.append(s)
return q
我們通過
len(p)
擷取運動的次數,之後分别計算正确/超調/不足的機率,并且求和以得到運動之後的機率分布。
可視化:
然後我們需要可視化我們的得到的分布:
def display_map(grid, bar_width=1):
if(len(grid) > 0):
x_labels = range(len(grid))
plt.bar(x_labels, height=grid, width=bar_width, color='b')
plt.xlabel('Grid Cell')
plt.ylabel('Probability')
plt.ylim(0, 1) # range of 0-1 for probability values
plt.title('Probability of the robot being at each cell in the grid')
plt.xticks(np.arange(min(x_labels), max(x_labels)+1, 1))
plt.show()
else:
print('Grid is empty')
通過python的
matplotlib
庫可以輕松的實作可視化,我們可以通過定義如下的
main
函數,整合上述的工作:
def main():
global p
for k in range(len(measurements)):
p = sense(p, measurements[k])
p = move(p, motions[k])
print (p)
display_map(p)
if __name__ == '__main__':
main()
我們甚至可以開啟matplotlib實時顯示功能,觀察如果我們運動1000次會有什麼結果:
def main():
global p
plt.ion()
for k in range(len(measurements)):
p = sense(p, measurements[k])
for i in range(1000):
p = move(p, motions[k])
plt.pause(0.05)
display_map(p, 0.9)
print (p)
Peek 2018-10-09 04-10.gif
三、總結一下
通過今天的這篇文章,我們介紹了一個最基本用于機器人定位的算法模型,并且使用結合了
Python
與
機率論
的隻是具體實作了它,别小看這個算法,他可是自動駕駛汽車定位的核心思想!
如果這篇文章幫助到了你,,請務必分享!!
四、源代碼擷取
請在下面留言郵箱或者關注公衆号背景回複郵箱即可。
不足之處,敬請斧正; 若你覺得文章還不錯,請關注微信公衆号“SLAM 技術交流”繼續支援我們,筆芯:D。