》介紹了TopK的四種解法,其中随機選擇 (randomized select) 最為經典,用減治法 (Reduce & Conquer) 的思想,将資料規模急速降低,總體複雜度為O(n)。
結尾挖了一個坑:求TopK,有沒有比随機選擇更快的方法呢?
空間換時間,是算法優化中最常見的手段,如果有相對充裕的記憶體,可以有更快的算法。
畫外音:即使記憶體不夠,也可以水準切分,使用分段的方法來操作,減少每次記憶體使用量。
TopK問題描述
從arr[1, 12]={5,3,7,1,8,2,9,4,7,2,6,6} 這n=12個數中,找出最大的k=5個。
比特位圖(bitmap)法
bitmap,是空間換時間的典型代表。它是一種,用若幹個bit來表示集合的資料結構。
例如,集合S={1,3,5,7,9},容易發現,S中所有元素都在1-16之間,于是,可以用16個bit來表示這個集合:存在于集合中的元素,對應bit置1,否則置0。
畫外音:究竟需要多少存存儲空間,取決于集合中元素的值域,在什麼範圍之内。
上述集合S,可以用1010101010000000這樣一個16bit的bitmap來表示,其中,第1, 3, 5, 7, 9個bit位置是1。
假設TopK的n個元素都是int,且元素之間沒有重複,隻需要申請2^32個bit,即4G的記憶體,就能夠用bitmap表示這n元素。
掃描一次所有n個元素,以生成bitmap,其時間複雜度是O(n)。生成後,取TopK隻需要找到最高位的k個bit即可。算法總時間複雜度也是O(n)。
僞代碼為:
bitmap[4G] = make_bitmap(arr[1, n]);
return bitmap[top k bits]; bitmap算法有個缺點,如果集合元素有重複,相同的元素會被去重,假設集合S中有5個1,最終S制作成bitmap後,這5個1隻對應1個bit位,相當于4個元素被丢掉了,這樣會導緻,找到的TopK不準。該怎麼優化呢?
比特位圖計數
優化方法是,每個元素的1個bit變成1個計數。
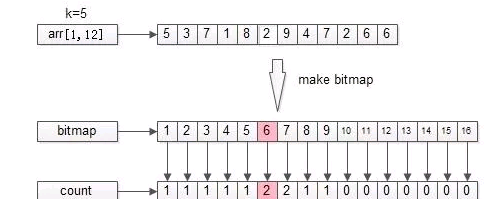
如上圖所示,TopK的集合經過比特位圖計數處理後,會記錄每個bit對應在集合S中出現過多少次。
接下來,找TopK的過程,就是bitmap從高位的計數開始,往低位的計數掃描,得到count之和等于k,對應的bit就是TopK所求。
如上圖所示,k=5:
(1)第一個非0的count是1,對應的bit是9;
(2)第二個非0的count也是1,對應的bit是8;
(3)第三個非0的count是2,對應的bit是7;
(4)第四個非0的count是2,對應的bit是6,但TopK隻缺1個數字了,故隻有1個6入選;
故,最終的TopK={9, 8, 7, 7, 6}。
結論:通過比特位圖精準計數的方式,求解TopK,算法整體隻需要不到2次掃描,時間複雜度為O(n),比減治法的随機選擇會更快。
為了鞏固今天的内容,例行挖個坑。
面試中,還有個問題問得比較多:求一個正整數的二進制表示包含多少個1?
例如:7的二進制表示是111,即7的二進制表示包含3個1。
畫外音:我面試過程中從不問這個問題。
最常見的解法是:
uint32_t count_one(uint32_t n){
uint32_t count=0;
while(n){
count ++;
n &= (n-1);
}
return count;
} 提問:還有多少種更快的方法呢?
原文釋出時間為:2018-09-25
本文作者:58沈劍
本文來自雲栖社群合作夥伴“
架構師之路”,了解相關資訊可以關注“
”