[劍指offer] 數組中的逆序對

本文首發于我的個人部落格： 尾尾部落

題目描述

在數組中的兩個數字，如果前面一個數字大于後面的數字，則這兩個數字組成一個逆序對。輸入一個數組,求出這個數組中的逆序對的總數P。并将P對1000000007取模的結果輸出。 即輸出P%1000000007

輸入描述:

題目保證輸入的數組中沒有的相同的數字

資料範圍：

對于%50的資料,size<=10^4

對于%75的資料,size<=10^5

對于%100的資料,size<=2*10^5
           

示例1

輸入

1,2,3,4,5,6,7,0

輸出

7

解題思路

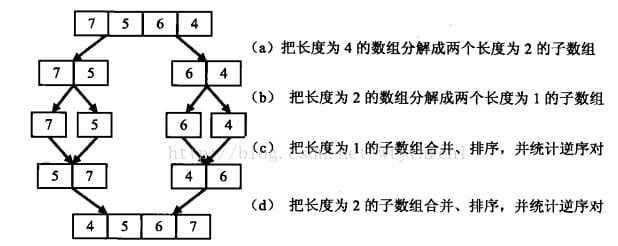
很容易想到的方法就是周遊每一個元素，讓其與後面的元素對比，如果大于則count++，但是這樣的時間複雜度是O(n^2)，是以，我們可以用歸并排序思路。

image

例如7,5,4,6可以劃分為兩段7,5和4,6兩個子數組

1. 在7,5中求出逆序對，因為7大于5是以有1對
2. 在6,4中求出逆序對，因為6大于4是以逆序對再加1，為2
3. 對7,5和6,4進行排序，結果為5,7,和4,6
4. 設定兩個指針分别指向兩個子數組中的最大值，p1指向7，p2指向6
5. 比較p1和p2指向的值，如果大于p2，因為p2指向的是最大值，是以第二個子數組中有幾個元素就有幾對逆序對(目前有兩個元素，逆序對加2,2+2=4)，7>6,比較完之後将p1指向的值放入輔助數組裡，輔助數組裡現在有一個數字7，然後将p1向前移動一位指向5
6. 再次判斷p1和p2指向的值，p1小于p2，因為p1指向的是第一個子數組中最大值，是以子數組中沒有能和目前p2指向的6構成逆序對的數，将p2指向的值放入輔助數組，并向前移動一位指向4，此時輔助數組内為6,7
7. 繼續判斷p1(指向5)和p2(指向4)，5>4,第二個子數組中隻有一個數字，逆序對加1，4+1=5，為5對，然後将5放入輔助數組，第一個子數組周遊完畢，隻剩下第二個子數組，目前隻有一個4，将4也放入輔助數組，函數結束。輔助數組此時為4,5,6,7.逆序對為5.

參考代碼

public class Solution {
    public int InversePairs(int [] array) {
        int len = array.length;
        if(array== null || len <= 0){
            return 0;
        }
        return mergeSort(array, 0, len-1);
    }
    public int mergeSort(int [] array, int start, int end){
        if(start == end)
            return 0;
        int mid = (start + end) / 2;
        int left_count = mergeSort(array, start, mid);
        int right_count = mergeSort(array, mid + 1, end);
        int i = mid, j = end;
        int [] copy = new int[end - start + 1];
        int copy_index = end - start;
        int count = 0;
        while(i >= start && j >= mid + 1){
            if(array[i] > array[j]){
                copy[copy_index--] = array[i--];
                count += j - mid;
                if(count > 1000000007){
                    count %= 1000000007;
                }
            }else{
                copy[copy_index--] = array[j--];
            }
        }
        while(i >= start){
            copy[copy_index--] = array[i--];
        }
        while(j >= mid + 1){
            copy[copy_index--] = array[j--];
        }
        i = 0;
        while(start <= end) {
            array[start++] = copy[i++];
        }
        return (left_count+right_count+count)%1000000007;
    }
}