0.參考資料
尊重他人的勞動成果,貼上參考的資料位址,本文僅作學習記錄之用。
- https://www.codeproject.com/Articles/869059/Topological-sorting-in-Csharp
- https://songlee24.github.io/2015/05/07/topological-sorting/
- https://www.cnblogs.com/skywang12345/p/3711483.html
1.介紹
自己之前并沒有接觸過拓撲排序,頂多聽說過拓撲圖。在寫前一篇文章的時候,看到 Abp 架構在處理子產品依賴項的時候使用了拓撲排序,來確定頂級節點始終是最先進行加載的。第一次看到覺得很神奇,看了一下維基百科頭也是略微大,自己的水準也是停留在冒泡排序的層次。ヽ(≧□≦)ノ
看了第二篇參考資料才大緻了解,在此記錄一下。
2.原理
先來一個基本定義:
在圖論中,拓撲排序(Topological Sorting)是一個有向無環圖(DAG, Directed Acyclic Graph)的所有頂點的線性序列。且該序列必須滿足下面兩個條件:
- 每個頂點出現且隻出現一次。
- 若存在一條從頂點 A 到頂點 B 的路徑,那麼在序列中頂點 A 出現在頂點 B 的前面。
有向無環圖(DAG)才有拓撲排序,非DAG圖沒有拓撲排序一說。
例如,有一個集合它的依賴關系如下圖:
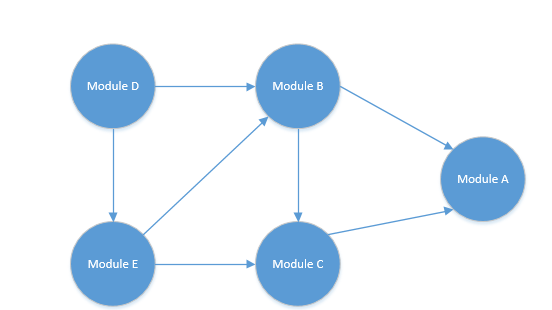
可以看到他有一個依賴關系:
- Module D 依賴于 Module E 與 Module B 。
- Module E 依賴于 Module B 與 Module C 。
- Module B 依賴于 Module A 與 Module C 。
- Module C 依賴于 Module A 。
- Module A 無依賴 。
這個就是一個 DAG 圖,我們要得到它的拓撲排序,一個簡單的步驟如下:
- 從 DAG 圖中選擇一個沒有前驅的頂點并輸出。
- 從 DAG 圖中删除該頂點,以及以它為起點的有向邊。
- 重複步驟 1、2 直到目前的 DAG 圖為空,或者目前圖不存在無前驅的頂點為止。
按照以上步驟,我們來進行一個排序試試。
最後的排序結果就是:
Module D -> Module E -> Module B -> Module C -> Module A
emmmm,其實一個有向無環圖可以有一個或者多個拓撲序列的,因為有的時候會存在一種情況,即以下這種情況:
這個時候你就可能會有這兩種結果
D->E->B->C->F->A
D->E->B->F->C->A
因為 F 與 C 是平級的,他們初始化順序即便不同也沒有什麼影響,因為他們的依賴層級是一緻的,不過細心的朋友可能會發現這個順序好像是反的,我們還需要将其再反轉一次。
3.實作
上面這種方法僅适用于已知入度的時候,也就是說這些内容本身就是存在于一個有向無環圖之中的,如果按照以上方法進行拓撲排序,你需要維護一個入度為 0 的隊列,然後每次疊代移除入度為 0 頂點所指向的頂點入度。
例如有以下圖:
按照我們之前的算法,
- 首先初始化隊列,将 5 與 4 這兩個入度為 0 的頂點加入隊列當中。
- 執行 While 循環,條件是隊列不為空。
- 之後首先拿出 4 。
- 然後針對其指向的頂點 0 與 頂點 1 的入度減去 1。
- 減去指向頂點入度的時候同時判斷,被減去入度的頂點其值是否為 0 。
- 這裡 1 入度被減去 1 ,為 0 ,添加到隊列。
- 0 頂點入度減去 1 ,為 1。
- 隊列現在有 5 與 1 這兩個頂點,循環判斷隊列不為空。
- 5 指向的頂點 0 入度 減去 1,頂點 0 入度為 0 ,插入隊列。
這樣反複循環,最終隊列全部清空,退出循環,得到拓撲排序的結果4, 5, 2, 0, 3, 1 。
4.深度優先搜尋實作
在參考資料 1 的代碼當中使用的是深度優先算法,它适用于有向無環圖。
有以下有向環圖 G2:
對上圖 G2 進行深度優先周遊,首先從入度為 0 的頂點 A 開始周遊:
它的步驟如下:
- 通路 A 。
- 通路 B 。
-
通路 C 。
在通路了 B 後應該是通路 B 的另外一個頂點,這裡可以是随機的也可以是有序的,具體取決于你存儲的序列順序,這裡先通路 C 。
- 通路 E 。
-
通路 D 。
這裡通路 D 是因為 B 已經被通路過了,是以通路頂點 D 。
-
通路 F 。
因為頂點 C 已經被通路過,是以應該回溯通路頂點 B 的另一個有向邊指向的頂點 F 。
- 通路 G 。
是以最後的通路順序就是 A -> B -> C -> E -> D -> F -> G ,注意順序還是不太對哦。
看起來跟之前的方法差不多,實作當中,其
Sort()
方法内部包含一個 visited 字典,用于标記已經通路過的頂點,sorted 則是已經排序完成的集合清單。
在字典裡 Key 是頂點的值,其 value 值用來辨別是否已經通路完所有路徑,為
true
則表示正在處理該頂點,為
false
則表示已經處理完成。
現在我們來寫實作吧:
public static IList<T> Sort<T>(IEnumerable<T> source, Func<T, IEnumerable<T>> getDependencies)
{
var sorted = new List<T>();
var visited = new Dictionary<T, bool>();
foreach (var item in source)
{
Visit(item, getDependencies, sorted, visited);
}
return sorted;
}
public static void Visit<T>(T item, Func<T, IEnumerable<T>> getDependencies, List<T> sorted, Dictionary<T, bool> visited)
{
bool inProcess;
var alreadyVisited = visited.TryGetValue(item, out inProcess);
// 如果已經通路該頂點,則直接傳回
if (alreadyVisited)
{
// 如果處理的為目前節點,則說明存在循環引用
if (inProcess)
{
throw new ArgumentException("Cyclic dependency found.");
}
}
else
{
// 正在處理目前頂點
visited[item] = true;
// 獲得所有依賴項
var dependencies = getDependencies(item);
// 如果依賴項集合不為空,周遊通路其依賴節點
if (dependencies != null)
{
foreach (var dependency in dependencies)
{
// 遞歸周遊通路
Visit(dependency, getDependencies, sorted, visited);
}
}
// 處理完成置為 false
visited[item] = false;
sorted.Add(item);
}
}
頂點定義:
// Item 定義
public class Item
{
// 條目名稱
public string Name { get; private set; }
// 依賴項
public Item[] Dependencies { get; set; }
public Item(string name, params Item[] dependencies)
{
Name = name;
Dependencies = dependencies;
}
public override string ToString()
{
return Name;
}
}
調用:
static void Main(string[] args)
{
var moduleA = new Item("Module A");
var moduleC = new Item("Module C", moduleA);
var moduleB = new Item("Module B", moduleC);
var moduleE = new Item("Module E", moduleB);
var moduleD = new Item("Module D", moduleE);
var unsorted = new[] { moduleE, moduleA, moduleD, moduleB, moduleC };
var sorted = Sort(unsorted, x => x.Dependencies);
foreach (var item in sorted)
{
Console.WriteLine(item.Name);
}
Console.ReadLine();
}
結果: