歡迎探讨,如有錯誤敬請指正
如需轉載,請注明出處 http://www.cnblogs.com/nullzx/
相關部落格:
從2-3-4樹到紅黑樹(中)
從2-3-4樹到紅黑樹(下)
1. 2-3-4樹的定義
2-3-4樹是一種階為4的B樹。它是一種自平衡的資料結構,可以保證在O(lgn)的時間内完成查找、插入和删除操作。它主要滿足以下性質:
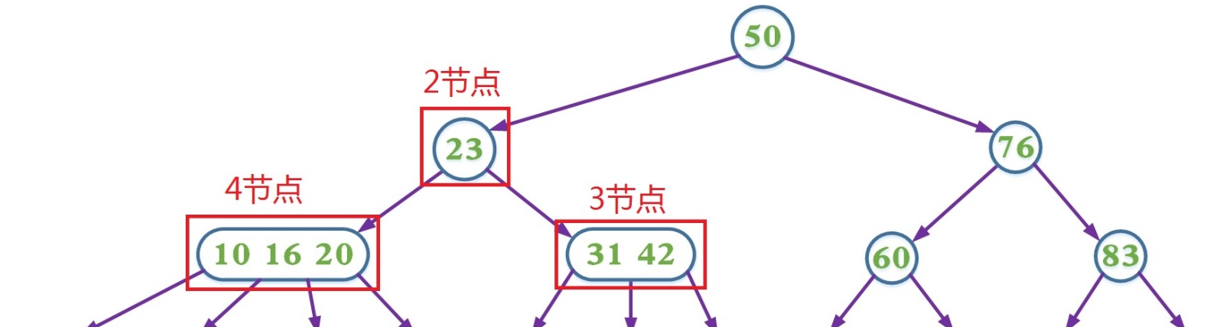
(1)每個節點每個節點有1、2或3個key,分别稱為2(孩子)節點,3(孩子)節點,4(孩子)節點。
(2)所有葉子節點到根節點的長度一緻(也就是說葉子節點都在同一層)。
(3)每個節點的key從左到右保持了從小到大的順序,兩個key之間的子樹中所有的
key一定大于它的父節點的左key,小于父節點的右key。
2. 插入操作
(1)如果2-3-4樹中已存在目前插入的key,則插入失敗,否則最終一定是在葉子節點中進行插入操作
(2)如果待插入的節點不是4節點,那麼直接在該節點插入
(3)如果待插入的節點是個4節點,那麼應該先分裂該節點然後再插入。一個4節點可以分裂成一個根節點和兩個子節點(這三個節點各含一個key)然後在子節點中插入,我們把分裂形成的根節點中的key看成向上層插入的key,然後重複第2步和第3步。
如果是在4節點中進行插入,每次插入會多出一個分支,如果插入操作導緻根節點分裂,則2-3-4樹會生長一層。
3. 删除操作
(1)如果2-3-4樹中不存在目前需要删除的key,則删除失敗。
(2)如果目前需要删除的key不位于葉子節點上,則用後繼key覆寫,然後在它後繼
key所在的子支中删除該後繼key。
(3)如果目前需要删除的key位于葉子節點上:
(3.1)該節點不是2節點,删除key,結束
(3.2)該節點是2節點,删除該節點:
(3.2.1)如果兄弟節點不是2節點,則父節點中的key下移到該節點,兄弟節點中的一個key上移
(3.2.2)如果兄弟節點是2節點,父節點是個3節點或4節點,父節點中的key與兄弟節點合并
(3.2.3)如果兄弟節點是2節點,父節點是個2節點,父節點中的key與兄弟節點中的key合并,形成一個3節點,把此節點看成目前節點(此節點實際上是下一層的節點),重複步驟3.2.1到3.2.3
如果是在2節點(葉子節點)中進行删除,每次删除會減少一個分支,如果删除操作導緻根節點參與合并,則2-3-4樹會降低一層。
4. 帶有預分裂的插入操作
上面的插入以及删除操作在某些情況需要不斷回溯來調整樹的結構以達到平衡。為了消除回溯過程,在插入操作過程中我們可以采取預分裂的操作,即我們在插入的搜尋路徑中,遇到4節點就分裂(分裂後形成的根節點的key要上移,與父節點中的key合并)這樣可以保證找到需要插入節點時可以直接插入(即該節點一定不是4節點)
5. 帶有預合并的删除操作
在删除過程中,我們同樣可以采取預合并的操作,即我們在删除的搜尋路徑中(除根節點,因為根節點沒有兄弟節點和父節點),遇到目前節點是2節點,如果兄弟節點也是2節點就合并(該節點的父節點中的key下移,與自身和兄弟節點合并);如果兄弟節點不是2節點,則父節點的key下移,兄弟節點中的key上移。這樣可以保證,找到需要删除的key所在的節點時可以直接删除(即要删除的key所在的節點一定不是2節點)。
這裡包含key為60的節點也可以選擇讓父節點中的key 76下移和兄弟節點中的83合并,兩種方式都能達到B樹的平衡,這也是在2-3-4樹對應的紅黑樹中使用的方式。