21.偏差和方差舉例
前提:對于人類而言,可以達到近乎完美的表現(即人類去做分類是誤差可以接近0)。
(1)假設算法的表現如下:訓練誤差率:1%,開發誤差率:11%;此時即為高方差(high variance),也被稱為過拟合(overfitting)。
(2)假設算法的表現如下:訓練誤差:15&,開發誤差率:16%;此時即為高偏差(high bias),也被稱為欠拟合(underfitting)。
(3)假設算法的表現如下:訓練誤差:15%,開發誤差率:30%;此時即為高偏差和高方差。
(4)假設算法的表現如下:訓練誤差:0.5%,開發誤差率:1%;此時算法已經非常完美。
22.與最優誤差率比較
舉例:當一個連人類都很難完成(如很多噪音的語音識别)的分類任務,人類的誤差率達到14%,此時最完美的誤差為14%,該誤差稱為最優誤差率,也稱為貝葉斯錯誤率(Bayes error rate)。以上的最優錯誤率是可以确定的,但是有些問題如電影推薦,很難去确定其最優誤差率是多少。
此時偏差和進一步細化:偏差=最優誤差率+可避免偏差;其中可避免偏差高時才值得去優化。
23..處理偏差和方差
(1)如果具有較高的可避免偏差,那麼可以加大模型的規模(例如增加神經元的層數、每層神經元的個數)。
(2)如果具有較高的方差,那麼可以向訓練集增加資料。
其他(3)改變網絡的架構,這樣會帶來新的結果。
在增大網絡模型時,會帶來高方差的風險,但隻要通過适當的正則化(如L2),或者dropout等政策,就不會出現這樣的問題。
24.偏差和方差間的均衡
在現如今,往往可以獲得足夠的資料,并且足夠的算力來支撐非常大的網絡,是以不會出現此消彼長的情況。
25.減少可避免偏差的技術
(1)加大模型規模(例如層數/神經元個數),此時加入正則化可以抵消方差的增加。
(2)根據誤差分析結果修改輸入特征。
(3)減少或者去除正則化。這種方式會增加方差。
(4)修改模型架構。這項技術會同時影響方差和偏差。
26.訓練集誤差分析
在訓練集上也做類似于開發集上的誤差分析。
27.減少方差的技術
(1)添加更多的訓練資料。
(2)加入正則化(L1,L2,Dropout),該項會增大偏差。
(3)加入提前終止(比如根據開發集提前終止梯度下降),這項技術會增加偏差,一些學者将其歸入正則化技術之一。
(4)通過特征選擇減少特征的數量和種類,當資料集很小時,特征選擇非常有用。
(5)減小模型規模,謹慎使用。
以下兩種方式和減少偏差的政策相同
(6)根據誤差分析結果修改輸入特征。
(7)修改模型架構。
28.診斷偏差與方差:學習曲線
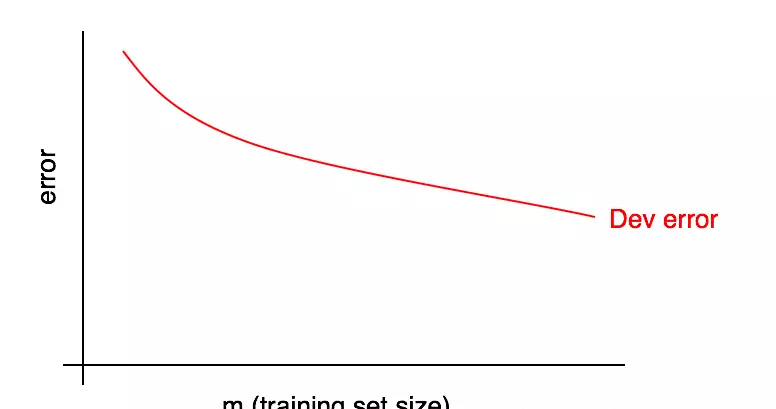
學習1曲線:誤差随資料量增加的變化趨勢。
學習曲線有一個缺點:當資料量變得越來越多是,将很難預測後續紅色曲線的走向。
29.繪制訓練誤差曲線
訓練誤差上升說明:比如兩張圖檔算法很容易就分辨出來,其誤差為0,當增加到100張時,就不一定都能正确識别了。
30.解讀學習曲線:高偏差
觀察結果:
(1)随着我們添加更多的訓練資料,訓練誤差隻會變得更糟,是以藍色的訓練誤差曲線隻會保持不動或上升,這表明它隻會遠離期望的性能水準(綠色的線)。
(2)紅色的開發誤差曲線通常要高于藍色的誤差曲線,是以隻要訓練誤差高于期望性能水準,通過添加更多資料來讓紅色開發誤差曲線下降到期望性能水準之下也基本不可能。
之前我們讨論的都是曲線的最右端,而通過學習曲線則更加的群面了解算法。