In Part II, we saw how Alice can blindly evaluate the hiding E(P(s)) of her polynomial P of degree d, at a point s belonging to Bob. We called this “blind” evaluation, because Alice did not learn s in the process.
在第二部分,我們知道了Alice如何在屬于Bob的 s 點,去盲評她d階多項式P的匿數E(P(s))。我們将其稱為 “盲” 評估,因為 Alice 在這個過程中并不知道 s。
However, there was something missing in that protocol – the fact that Alice is able to compute E(P(s)) does not guarantee she will indeed send E(P(s)) to Bob, rather than some completely unrelated value.
然而,在那項協定中有瑕疵 – 雖然Alice 能夠計算出 E(P(s)) ,但并不能確定她将正确 E(P(s)) 發送給 Bob,而非一些完全不相關的值。
Thus, we need a way to “force” Alice to follow the protocol correctly. We will explain in part IV precisely how we achieve this. In this post, we focus on explaining the basic tool needed for that – which we call here the Knowledge of Coefficient (KC) Test.
是以,我們需要一種 “強制” Alice 正确地遵從協定的方式。我們将在第四部分詳細解釋我們如何實作這一點。在本文中,我們專注在解釋實作這一功能需要用到的基礎工具 – 我們将其稱為 “知識系數(KC)測試”。
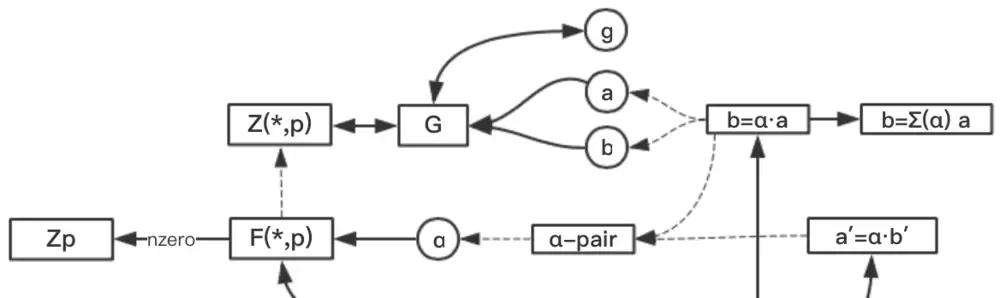
As before, we denote by g a generator of a group G of order |G|=p where the discrete log is hard. It will be convenient from this post onwards to write our group additively rather than multiplicatively. That is, for α ∈ Fp, α⋅g denotes the result of summing α copies of g.
正如之前一樣,我們使用 g 表示一個階為|G|=p的群G的生成器,對于該群,離散對數是困難的。在文章開始時使用加法而不是乘法解釋起來更加友善。 那就是,對于 α∈Fp ,α⋅g 表示 α 個 g 的求和結果。
THE KC TEST
知識系數(KC)測試
For α ∈ F(∗,p) [1], let us call a pair of elements (a,b) in G an α-pair if a,b≠0 and b=α⋅a.
[1] F(∗,p) denotes the non-zero elements of Fp. It is the same as Z(∗,p) described in Part I.
The KC Test proceeds as follows.
- Bob chooses random α ∈ F(∗,p) and a ∈ G. He computes b=α⋅a.
- He sends to Alice the “challenge” pair (a,b). Note that (a,b) is an α-pair.
- Alice must now respond with a different pair (a′,b′) that is also an α-pair.
- Bob accepts Alice’s response only if (a′,b′) is indeed an α-pair. (As he knows α he can check if b′=α⋅a′.)
對于 α∈F(∗,p)[1], 如果 a,b≠0 和 b=α⋅a 同時成立,則我們稱 G 中的一組元素 (a,b) 為 α-pair。
- F(∗,p) 表示 Fp 中的非零元素組成的集合,它與第一部分描述的 Z(∗,p) 相類似。
知識系數(KC)測試按照如下的步驟進行:
- Bob 随機選擇一個 α∈F(∗,p) 和 a∈G 。他計算出 b=α⋅a 。
- 他發送 “挑戰” 數對 (a,b) 給 Alice。注意,(a,b) 是一個 α-pair 。
- Alice 現在必須回複一個不同的數對 (a′,b′) 同時也必須是 α-pair 。
- 如果 (a′,b′) 确實是一個 α-pair ,則 Bob 接受 Alice 的回複。(由于他知道 α ,他可以檢查 b′=α⋅a′是否成立。)
Now, let’s think how Alice could successfully respond to the challenge. Let’s assume for a second that she knew α. In that case, she could simply choose any a′ in G, and compute b′=α⋅a′; and return (a′,b′) as her new α-pair.
現在,讓我們思考 Alice 如何成功地回複挑戰。 讓我們假設一下,她知道 α 。 在這種情況下,她便可以在 G 中簡單地挑選出 a′,并計算出 b′=α⋅a′; 同時傳回 (a′,b′) 作為她得到的新 α-pair 。
However, as the only information about α she has is α⋅a and G has a hard discrete log problem, we expect that Alice cannot find α.
然而,由于 Alice 唯一擁有關于α的資訊的載體是α⋅a ,并且 G 具有難離散對數問題,我們可以預計 Alice 并不能得到 α。
So how can she successfully respond to the challenge without knowing α?
是以,如何讓 Alice 在不知道 α 的前提下成功回複挑戰呢?
Here’s the natural way to do it: Alice simply chooses some γ∈F∗p,γ∈Fp∗, and responds with (a′,b′)=(γ⋅a,γ⋅b).(a′,b′)=(γ⋅a,γ⋅b).
In this case, we have:
b′=γ⋅b=γα⋅a=α(γ⋅a)=α⋅a′,b′=γ⋅b=γα⋅a=α(γ⋅a)=α⋅a′,
so indeed (a′,b′)(a′,b′) is an αα-pair as required.
以下是實作這一目标的自然做法: Alice 簡單地選擇一些 γ∈F(∗,p),并且回複 (a′,b′)=(γ⋅a,γ⋅b) 。
在這種情況下,我們有:
b′=γ⋅b=γα⋅a=α(γ⋅a)=α⋅a′,
是以(a′,b′)确實是這裡需要的 α-pair 。
Note that if Alice responds using this strategy, she knows the ratio between a and a′. That is, she knows the coefficient γ such that a′=γ⋅a.
注意到,如果 Alice 使用這種政策進行回複,她就知道 a 和 a′ 之間的比率。 也就是說,她知道系數 γ 滿足 a′=γ⋅a 。
The Knowledge of Coefficient Assumption [2] (KCA) states that this is always the case, namely:
This is typically called the Knowledge of Exponent Assumption in the literature, as traditionally it was used for groups written multiplicatively.
KCA: If Alice returns a valid response (a′,b′) to Bob’s challenge (a,b) with non-negligible probability over Bob’s choices of a,α, then she knows γ such that a′=γ⋅a.
The KC Test and Assumption will be important tools in Part IV.
知識系數假設 [2] (KCA) 指出,情況總是像這樣:
- 它的書面名稱通常為知識系數假設,傳統上被用在字面乘法性質的群上。
KCA: 如果 Alice 對于Bob選擇的a,α,以不可忽略的可能性,對Bob的挑戰(a,b)**給出一個有效的回複 (a′,b′),此時,她所知道的 γ ,可以滿足 a′=γ⋅a 。
知識系數(KC)測試和假設将是第四部分的重要工具。
WHAT DOES “ALICE KNOWS” MEAN EXACTLY
“ALICE知道”的确切意義是什麼
You may wonder how we can phrase the KCA in precise mathematical terms; specifically, how do we formalize the notion that “Alice knows γ” in a mathematical definition?
你也許會好奇我們如何将 KCA 用準确地數學形式表達出來;具體來說,我們如何用數學定義将 “Alice 知道 γ” 的意義形式化出來?
This is done roughly as follows: We say that, in addition to Alice, we have another party which we call Alice’s Extractor. Alice’s Extractor has access to Alice’s inner state.
我們通過下面這樣粗略的方式說明: 我們說,除了 Alice 之外,我們有一個被稱為 Alice的提取器 的角色。 Alice的提取器可以通路 Alice 的内部狀态。
We then formulate the KCA as saying that: whenever Alice successfully responds with an α-pair (a′,b′), Alice’s Extractor outputs γ such that a′=γ⋅a. [3]
[3]The fully formal definition needs to give the Extractor “a little slack” and states instead that the probability that Alice responds successfully but the Extractor does not output such γ is negligible.
我們這時便可以這樣形式化 KCA: 當 Alice 使用一個 α-pair (a′,b′) 成功回複時,Alice的提取器 輸出的 γ 滿足 a′=γ⋅a. [3]
- 完整正式定義需要讓提取器 “稍微松懈一下”,并反過來聲明,Alice 成功回複但是提取器無法正常輸出這樣的 γ 的可能性可以忽略不計。
譯者總結
數學關系
互動模型