Abstract
上一節:z-buffer & 紋理映射
從正交投影到透視投影。
如果你對投影幾何沒什麼概念,可以移步 這裡 。
Reference :
- https://github.com/ssloy/tinyrenderer/wiki/Lesson-4-Perspective-projection
在移步到投影幾何之前,回憶之前渲染的場景,是基于正交投影計算的。
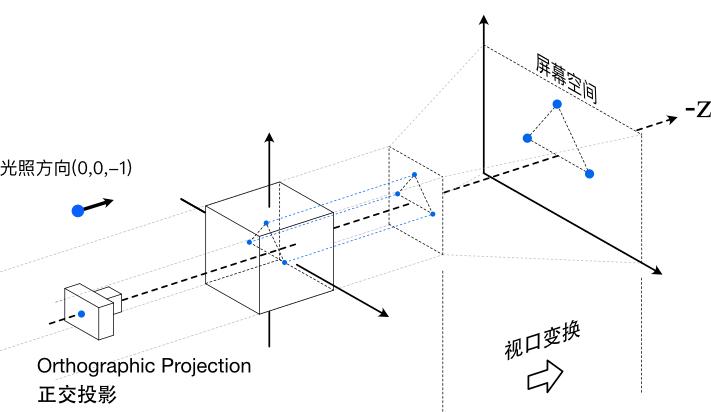
也即,導入模型的頂點已經在 \([-1, 1]^{3}\) 範圍中,隻需要将頂點映射至螢幕空間再光栅化即可。
但對于更真實的情況 --- 人眼或者說相機的實際成像原理為透視投影。
線性變換
線性變換的原理
普通笛卡爾平面上的線性變換可由一個對應的矩陣表示。設有 \(P^2\) 平面的笛卡爾坐标 \((x, y)\),它的線性變換可以寫成:
\(\left[\begin{array}{cc} a & b \\ c & d \end{array}\right]\left[\begin{array}{c} x \\ y \end{array}\right] = \left[\begin{array}{c} ax + by \\ cx + dy \end{array}\right]\)
最簡單的變換由機關矩陣表示:
\(\left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{c} x \\ y \end{array}\right] = \left[\begin{array}{c} x \\ y \end{array}\right]\)
矩陣左對角線上的系數會對線性空間的基産生縮放作用:
\(\left[\begin{array}{cc} 1.5 & 0 \\ 0 & 1.5 \end{array}\right]\left[\begin{array}{c} x \\ y \end{array}\right] = \left[\begin{array}{c} 1.5x \\ 1.5y \end{array}\right]\)
讓我們用代碼來感受一下線性變換的魅力。這裡有另一個"正方體"(之是以打引号,是因為它缺少一個右上角)obj模型,我們将它的正面放在螢幕空間的中心并繪制出來,為了展現“中心”,再畫出 \(xy\) 坐标軸。
檢查一下它的頂點,正好是CVV空間的邊界:(你若對CVV沒什麼概念,請移步 這裡 ,在标準圖形管線流程中,預備映射到螢幕空間上的頂點是處于一個 \([-1, 1]^3\) 的正方體中的,就像本篇開頭的那個示意圖一樣)
v -1 -1 1
v 1 -1 1
v 1 0 1
v 0 1 1
v -1 1 1
v 1 1 0
v -1 -1 -1
v 1 -1 -1
v 1 1 -1
v -1 1 -1
也就是說,如果将這個"正方體"進行視區變換後,它的邊界會正好處于圖像邊緣,看不太清楚:
但是若将視區變換修改一下,也即将視區範圍縮小一點,就能适合觀察了。在我們現在的代碼中,視區變換現在由矩陣運算來完成:(若你對視區變換概念不強,請移步此文章的後半部分推導)
// 将[-1,1]^2中的點變換到以(x,y)為原點,w,h為寬與高的螢幕區域内
Matrix viewport(int x, int y, int w, int h) {
Matrix m = Matrix::identity(4);
m[0][3] = x + w/2.f;
m[1][3] = y + h/2.f;
m[2][3] = depth/2.f;
m[0][0] = w/2.f;
m[1][1] = h/2.f;
m[2][2] = depth/2.f;
return m;
}
目前顯示不清楚的視區矩陣調用是這樣的:
Matrix VP = viewport(0, 0, width, height);
也即将 \([-1, -1]^2\) 這個正方形範圍的中心移至螢幕空間中心,其寬高縮放為和螢幕一樣:
但若将矩陣調用修改一下:
Matrix VP = viewport(width/4, height/4, width/2, height/2);
視區便會被正确縮小:
當繪制結果利于觀察後,我們便可以嘗試一下對“正方體”進行兩個線性變換(黃線繪制的為其變換後結果):
- 縮放1.5倍
Matrix T = zoom(1.5);
- 平移并繞z軸旋轉
Matrix T = translation(Vec3f(.33, .5, 0))*rotation_z(cos(10.*M_PI/180.), sin(10.*M_PI/180.));
- Shear 錯切操作
效果是讓圖像往某個坐标軸上的方向傾斜。
\(\left[\begin{array}{cc} 1 & \frac{1}{3} \\ 0 & 1 \end{array}\right]\left[\begin{array}{c} x \\ y \end{array}\right] = \left[\begin{array}{c} x + \frac{y}{3} \\ y \end{array}\right]\)
Matrix T = Matrix::identity(4);
T[0][1] = 0.333;
用透視投影來表示3D空間
在TinyRender此節,我們使用一種特殊的透視投影,将投影平面設為 \(z = 0\)。
設投影機坐标 \((0, 0, c)\) ,待投影點 \(P(x, y, z)\) ,投影點 \(P^{'}(x^{'}, y^{'}, z^{'})\)。
由相似三角形:
\(\frac{x}{c - z} = \frac{x^{'}}{c},\ \ \ (1)\\\\
\frac{y}{c - z} = \frac{y^{'}}{c},\ \ \ (2)\)
可推出 \(x^{'} = \frac{x}{1 - \frac{z}{c}}\) ;\(y^{'} = \frac{y}{1 - \frac{z}{c}}\)
那麼便可以在将頂點變為螢幕坐标之前為它們乘一個透視變換矩陣:
\(\left[\begin{array}{cccc}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & -\frac{1}{c} & 1\end{array}\right]\)
它正好可以将頂點變成我們推導的 \(P^{'}\) 那樣。
不過值得注意的是,這種透視投影計算方式,僅考慮了 \(z \ge 0\) 内的頂點,\(z \lt 0\) 的點同樣會受到變換矩陣影響,但由于它們根本沒在我們數學模組化範圍内,是以變成什麼樣根本沒人知道。
但幸好有 z-buffer,\(z\) 值不受透視變換的影響,是以計算覆寫關系的時候 \(z \ge 0\) 内的頂點 一定能覆寫後面的點,是以出錯的點不會被我們看到。
掃描線算法用來進行 \(uv\) 插值
重心坐标配合包圍盒來進行插值與光栅化是較為常見的手段,現在介紹用掃描線算法進行插值的思想。
回憶 三角形光栅化 此章。我們得到三角形的三個頂點後,用掃描線三線性插值法來得到三角形内部的所有點。
這對于 \(uv\) 插值同樣适用,因為三角形三個頂點同樣對應三個 \(uv\) 坐标,隻需為 \(uv\) 坐标采取同樣的采樣算法即可。(注意掃描線算法要對三頂點 \(y\) 的順序進行排序,對它們對應的 \(uv\) 同樣需要)
void triangle(Vec3i t0, Vec3i t1, Vec3i t2, Vec2i uv0, Vec2i uv1, Vec2i uv2, TGAImage &image, float intensity, int *zbuffer) {
if (t0.y==t1.y && t0.y==t2.y) return; // 處理三角形退化情況
if (t0.y>t1.y) { std::swap(t0, t1); std::swap(uv0, uv1); }
if (t0.y>t2.y) { std::swap(t0, t2); std::swap(uv0, uv2); }
if (t1.y>t2.y) { std::swap(t1, t2); std::swap(uv1, uv2); }
int total_height = t2.y-t0.y;
for (int i=0; i<total_height; i++) {
bool second_half = i>t1.y-t0.y || t1.y==t0.y;
int segment_height = second_half ? t2.y-t1.y : t1.y-t0.y;
float alpha = (float)i/total_height; // 第一次線性插值
float beta = (float)(i-(second_half ? t1.y-t0.y : 0))/segment_height; // 第二次線性插值
Vec3i A = t0 + Vec3f(t2-t0 )*alpha;
Vec3i B = second_half ? t1 + Vec3f(t2-t1 )*beta : t0 + Vec3f(t1-t0 )*beta;
Vec2i uvA = uv0 + (uv2-uv0)*alpha;
Vec2i uvB = second_half ? uv1 + (uv2-uv1)*beta : uv0 + (uv1-uv0)*beta;
if (A.x>B.x) { std::swap(A, B); std::swap(uvA, uvB); }
for (int j=A.x; j<=B.x; j++) {
float phi = B.x==A.x ? 1. : (float)(j-A.x)/(float)(B.x-A.x); // 第三次線性插值
Vec3i P = Vec3f(A) + Vec3f(B-A)*phi;
Vec2i uvP = uvA + (uvB-uvA)*phi;
int idx = P.x+P.y*width;
if (zbuffer[idx]<P.z) {
zbuffer[idx] = P.z;
TGAColor color = model->diffuse(uvP);
image.set(P.x, P.y, TGAColor(color.r*intensity, color.g*intensity, color.b*intensity));
}
}
}
}
最後,應用了透視投影法後,可以得到一個較為真實的渲染視角
輸出相應的 z-buffer :
可以看到,離螢幕較近的部分越亮,離螢幕越遠的部分越暗,這符合深度緩存的原理。