八、随機性
原文: Randomness 譯者: 飛龍 協定: CC BY-NC-SA 4.0 自豪地采用 谷歌翻譯
在前面的章節中,我們開發了深入描述資料所需的技能。 資料科學家也必須能夠了解随機性。 例如,他們必須能夠随機将個體配置設定到實驗組和對照組,然後試圖說明,觀察到的兩組結果之間的差異是否僅僅是由于随機配置設定,或真正由于實驗所緻。
在這一章中,我們開始分析随機性。 首先,我們将使用 Python 進行随機選擇。 在
numpy
中有一個叫做
random
的子子產品,它包含許多涉及随機選擇的函數。 其中一個函數稱為
choice
。 它從一個數組中随機選取一個項目,選擇任何項目都是等可能的。 函數調用是
np.random.choice(array_name)
,其中
array_name
是要從中進行選擇的數組的名稱。
是以,下面的代碼以 50% 的幾率求值為
treatment
,50% 的機率為
control
。
two_groups = make_array('treatment', 'control')
np.random.choice(two_groups)
'treatment' 上面的代碼和我們迄今運作的所有其他代碼之間的巨大差異在于,上面的代碼并不總是傳回相同的值。 它可以傳回
treatment
或
control
,我們不會提前知道會選擇哪一個。 我們可以通過提供第二個參數來重複這個過程,它是重複這個過程的次數。
np.random.choice(two_groups, 10)
array(['treatment', 'control', 'treatment', 'control', 'control',
'treatment', 'treatment', 'control', 'control', 'control'],
dtype='<U9') 随機事件的根本問題是它們是否發生。 例如:
- 個體是否被配置設定到實驗組?
- 賭徒是否會赢錢?
- 一個民意調查是否做出了準确的預測?
一旦事件發生,你可以對所有這些問題回答“是”或“否”。 在程式設計中,通常通過将語句标記為
True
False
來執行此操作。 例如,如果個體被配置設定到實驗組,那麼“個體被配置設定到實驗組”的陳述将是真的。 如果不是,那将是假的。
布爾值和比較
在 Python 中,布爾值(以邏輯學家 George Boole 命名)表示真值,并隻有兩個可能的值:
True
和
False
。 無論問題是否涉及随機性,布爾值通常都由比較運算符産生。 Python 包含了各種比較值的運算符。 例如,
3
大于
1 + 1
3 > 1 + 1
True True
表示比較是有效的;Python 已經證明了
3
1 + 1
的關系的這個簡單事實。 下面列出了一整套通用的比較運算符。
| 比較 | 運算符 | True 示例 | False 示例 |
|---|---|---|---|
| 小于 | | | |
| | | |
| 小于等于 | | | |
| 大于等于 | | | |
| 等于 | | | |
| 不等于 | | | |
注意比較中的兩個等号
==
用于确定相等性。 這是必要的,因為 Python 已經使用
=
來表示名稱的指派,我們之前看到過。 它不能将相同的符号用于不同的目的。 是以,如果你想檢查
5
是否等于
10/2
,那麼你必須小心:
5 = 10/
2傳回一個錯誤資訊,因為 Python 假設你正試圖将表達式
10/2
的值賦給一個名稱,它是數字
5
。相反,你必須使用
5 == 10/2
,其計算結果為
True
5 = 10/2
File "<ipython-input-4-5c7d3e808777>", line 1
5 = 10/2
^
SyntaxError: can't assign to literal
5 == 10/2
True 一個表達式可以包含多個比較,并且它們都必須滿足,為了整個表達式為真。 例如,我們可以用下面的表達式表示
1 + 1
在
1
3
之間。
1 < 1 + 1 < 3
True 兩個數字的平均值總是在較小的數字和較大的數字之間。 我們用下面的數字
x
y
來表示這種關系。 你可以嘗試不同的
x
y
值來确認這種關系。
x = 12
y = 5
min(x, y) <= (x+y)/2 <= max(x, y)
True 字元串比較
字元串也可以比較,他們的順序是字典序。 較短的字元串小于以較短的字元串開頭的較長的字元串。
'Dog' > 'Catastrophe' > 'Cat' 我們回到随機選擇。 回想一下由兩個元素組成的數組
two_groups
,
treatment
control
。 為了看一個随機配置設定的個體是否去了實驗組,你可以使用比較:
np.random.choice(two_groups) == 'treatment'
False 和以前一樣,随機選擇并不總是一樣的,是以比較的結果也不總是一樣的。 這取決于是選擇
treatment
還是
control
。 對于任何涉及随機選擇的單元格,多次運作單元格來獲得結果的變化是一個好主意。
比較數組和值
回想一下,我們可以對數組中的很多數字執行算術運算。 例如,
make_array(0, 5, 2)*2
等同于
make_array(0, 10, 4)
。 以類似的方式,如果我們比較一個數組和一個值,則數組的每個元素都與該值進行比較,并将比較結果求值為布爾值數組。
tosses = make_array('Tails', 'Heads', 'Tails', 'Heads', 'Heads')
tosses == 'Heads'
array([False, True, False, True, True], dtype=bool) numpy
方法
count_nonzero
計算數組的非零(即
True
)元素的數量。
np.count_nonzero(tosses == 'Heads')
3 條件語句
在許多情況下,行動和結果取決于所滿足的一組特定條件。例如,随機對照試驗的個體如果被配置設定給實驗組,則接受實驗。賭徒如果赢了賭注就賺錢。
在本節中,我們将學習如何使用代碼來描述這種情況。條件語句是一個多行語句,它允許 Python 根據表達式的真值選擇不同的選項。雖然條件語句可以出現在任何地方,但它們通常出現在函數體内,以便根據參數值執行可變的行為。
條件語句總是以
if
開頭,這是一行,後面跟着一個縮進的主體。隻有當
if
後面的表達式(稱為
if
表達式)求值為真時,才會執行主體。如果
if
表達式的計算結果為
False
,則跳過
if
的主體。
讓我們開始定義一個傳回數字元号的函數。
def sign(x):
if x > 0:
return 'Positive'
sign(3)
'Positive' 如果輸入是正數,則此函數傳回正确的符号。 但是,如果輸入不是正數,那麼
if
false
,是以
return
語句被跳過,函數調用沒有值(為
None
)。
sign(-3) 是以,讓我們改進我們的函數來傳回負數,如果輸入是負數。 我們可以通過添加一個
elif
子句來實作,其中
elif
是 Python 的
else, if
的縮寫。
def sign(x):
if x > 0:
return 'Positive'
elif x < 0:
return 'Negative' 現在當輸入為
-3
時,
sign
傳回正确答案。
sign(-3)
'Negative' 那麼如果輸入是
呢?為了處理這個情況,我們可以添加
elif
子句:
def sign(x):
if x > 0:
return 'Positive'
elif x < 0:
return 'Negative'
elif x == 0:
return 'Neither positive nor negative'
sign(0)
'Neither positive nor negative' 與之等價,我們可以用
else
子句替換最後的
elif
子句,隻有前面的所有比較都是
false
,才會執行它的正文。 也就是說,輸入值等于
的時候。
def sign(x):
if x > 0:
return 'Positive'
elif x < 0:
return 'Negative'
else:
return 'Neither positive nor negative'
sign(0)
'Neither positive nor negative' 一般形式
條件語句也可以有多個具有多個主體的子句,隻有其中一個主體可以被執行。 多子句的條件語句的一般格式如下所示。
if <if expression>:
<if body>
elif <elif expression 0>:
<elif body 0>
elif <elif expression 1>:
<elif body 1>
...
else:
<else body> 總是隻有一個
if
子句,但是可以有任意數量的
elif
子句。 Python 将依次求解頭部的
if
elif
表達式,直到找到一個真值,然後執行相應的主體。
else
子句是可選的。 當提供
else
頭部時,隻有在前面的子句的頭部表達式都不為真時才執行
else
頭部。
else
子句必須總是在最後(或根本沒有)。
示例:”另一個”
現在我們将使用條件語句來定義一個看似相當虛假和對立的函數,但是在本章後面的章節中會變得友善。 它需要一個數組,包含兩個元素(例如,
red
blue
),以及另一個用于比較的元素。 如果該元素為
red
,則該函數傳回
blue
。 如果元素是(例如)
blue
,則函數傳回
red
。 這就是為什麼我們要将函數稱為
other_one
def other_one(x, a_b):
"""Compare x with the two elements of a_b;
if it is equal to one of them, return the other one;
if it is not equal to either of them, return an error message.
"""
if x == a_b.item(0):
return a_b.item(1)
elif x == a_b.item(1):
return a_b.item(0)
else:
return 'The input is not valid.'
colors = make_array('red', 'blue')
other_one('red', colors)
'blue'
other_one('blue', colors)
'red'
other_one('potato', colors)
'The input is not valid.' 疊代
程式設計中經常出現這樣的情況,特别是在處理随機性時,我們希望多次重複一個過程。 例如,要檢查
np.random.choice
是否實際上是随機選取的,我們可能需要多次運作下面的單元格,以檢視
Heads
是否以大約 50% 的幾率出現。
np.random.choice(make_array('Heads', 'Tails'))
'Heads' 我們可能希望重新運作代碼,帶有稍微不同的輸入或其他稍微不同的行為。 我們可以多次複制粘貼代碼,但是這很枯燥,容易出現拼寫錯誤,如果我們想要這樣做一千次或一百萬次,忘記它吧。
更自動化的解決方案是使用
for
語句周遊序列的内容。 這被稱為疊代。
for
語句以單詞
for
開頭,後面跟着一個名字,我們要把這個序列中的每個項目賦給它,後面跟着單詞
in
,最後以一個表達式結束,它求值為一個序列。 對于序列中的每個項目,
for
語句的縮進主體執行一次。
for i in np.arange(3):
print(i)
0
1
2 想象一下,沒有
for
語句的情況下,完全實作
for
語句功能的代碼,這樣很有幫助。 (這被稱為循環展開。)
for
語句簡單地複制了内部的代碼,但是在每次疊代之前,它從給定的序列中将我們選擇的名稱賦為一個新的值。 例如,以下是上面循環的展開版本:
i = np.arange(3).item(0)
print(i)
i = np.arange(3).item(1)
print(i)
i = np.arange(3).item(2)
print(i)
0
1
2 譯者注:實際的實作方式不是這樣,但是效果一樣。這裡不做深究。
請注意,我的名字是任意的,就像我們用
=
指派的名字一樣。
在這裡我們用一個更為現實的方式使用
for
語句:我們從數組中列印
5
個随機選項。
coin = make_array('Heads', 'Tails')
for i in np.arange(5):
print(np.random.choice(make_array('Heads', 'Tails')))
Heads
Heads
Tails
Heads
Heads 在這種情況下,我們隻執行了幾次完全相同的(随機)操作,是以我們
for
語句中的代碼實際上并不涉及到
i
擴充數組
雖然上面的
for
語句确實模拟了五次硬币投擲的結果,但結果隻是簡單地列印出來,并不是我們可以用來計算的形式。 是以,
for
語句的典型用法是建立一個結果數組,每次都擴充它。
numpy
中的
append
方法可以幫助我們實作它。 調用
np.append(array_name,value)
将求出一個新的數組,它是由
value
擴充的
array_name
。在使用
append
時請記住,數組的所有條目必須具有相同的類型。
pets = make_array('Cat', 'Dog')
np.append(pets, 'Another Pet')
array(['Cat', 'Dog', 'Another Pet'],
dtype='<U11') 這會使
pets
數組保持不變。
pets
array(['Cat', 'Dog'],
dtype='<U3') 但是在擴充數組的時候,通常使用
for
循環來修改它很友善。 這通過将擴充後的數組賦給原始數組的相同名稱來實作。
pets = np.append(pets, 'Another Pet')
pets
array(['Cat', 'Dog', 'Another Pet'],
dtype='<U11') 示例:計算正面的數量
現在我們可以模拟一個硬币的五次投擲,并把結果放入一個數組中。 我們将從建立一個空數組開始,然後附加每次投擲的結果。
coin = make_array('Heads', 'Tails')
tosses = make_array()
for i in np.arange(5):
tosses = np.append(tosses, np.random.choice(coin))
tosses
array(['Tails', 'Heads', 'Tails', 'Heads', 'Tails'],
dtype='<U32') 讓我們将
for
語句展開,重寫單元格。
coin = make_array('Heads', 'Tails')
tosses = make_array()
i = np.arange(5).item(0)
tosses = np.append(tosses, np.random.choice(coin))
i = np.arange(5).item(1)
tosses = np.append(tosses, np.random.choice(coin))
i = np.arange(5).item(2)
tosses = np.append(tosses, np.random.choice(coin))
i = np.arange(5).item(3)
tosses = np.append(tosses, np.random.choice(coin))
i = np.arange(5).item(4)
tosses = np.append(tosses, np.random.choice(coin))
tosses
array(['Heads', 'Heads', 'Tails', 'Tails', 'Heads'],
dtype='<U32') 通過将結果捕獲到數組中,我們自己有能力使用數組方法進行計算。 例如,我們可以使用
np.count_nonzero
來計算五次投擲中的正面數量。
np.count_nonzero(tosses == 'Heads')
2 疊代是一個強大的技術。 例如,通過為 1000 次投擲運作完全相同的代碼,而不是
5
次,我們可以計算
1000
次投擲的正面數量。
tosses = make_array()
for i in np.arange(1000):
tosses = np.append(tosses, np.random.choice(coin))
np.count_nonzero(tosses == 'Heads')
481 示例:100 次投擲中的正面數量
預測 100 次硬币投擲中有 50 個正面是很自然的,或多或少。
但多少是“或多或少”呢? 獲得正好 50 個正面的幾率是多少? 像資料科學這樣的問題,不僅因為它們涉及随機性的有趣方面,而且因為它們可以用于分析試驗,其中實驗和控制組的配置設定由硬币的投擲決定。
在這個例子中,我們将模拟以下實驗的 10,000 次重複:
- 擲硬币 100 次,記錄正面數量。
我們的結果的直方圖會讓我們了解有多少個正面。
作為一個預熱,請注意,
np.random.choice
接受可選的第二個參數來指定選擇的數量。 預設情況下,選擇使用替換來進行。 這裡是一個硬币 10 次投擲的模拟:
np.random.choice(coin, 10)
array(['Tails', 'Heads', 'Heads', 'Tails', 'Tails', 'Heads', 'Tails',
'Tails', 'Heads', 'Tails'],
dtype='<U5') 現在我們來研究 100 次投擲。 我們将首先建立一個名為
heads
的空數組。 然後,在每個一萬次重複中,我們會抛硬币 100 次,計算正面的數量,并将其附加到
heads
上。
N = 10000
heads = make_array()
for i in np.arange(N):
tosses = np.random.choice(coin, 100)
heads = np.append(heads, np.count_nonzero(tosses == 'Heads'))
heads
array([ 46., 64., 59., ..., 56., 54., 56.]) 讓我們将結果收集到表格中,并繪制直方圖:
results = Table().with_columns(
'Repetition', np.arange(1, N+1),
'Number of Heads', heads
)
results | Repetition | Number of Heads |
|---|---|
| 1 | 46 |
| 2 | 64 |
| 3 | 59 |
| 4 | 57 |
| 5 | 54 |
| 6 | 47 |
| 7 | 45 |
| 8 | 50 |
| 9 | 44 |
| 10 |
(省略了 9990 行)
這裡是資料的直方圖,桶的寬度為 1,中心為每個正面數量的值。
results.select('Number of Heads').hist(bins=np.arange(30.5, 69.6, 1)) 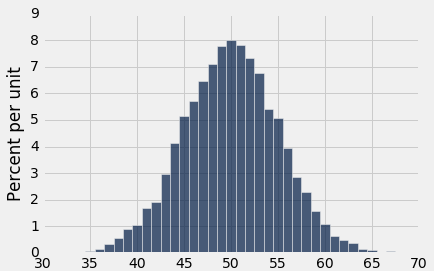
毫不奇怪,直方圖看起來大約關于 50 個正面左右對稱。 50 處的條形的高度大約是每機關 8%。 由于每個條形的寬度都是 1 個機關,這就是說,8% 的重複正好産生了 50 個正面。 這不是一個很大的百分比,但是與其他數量的正面相比,這是最大的。
直方圖還顯示,在幾乎所有的重複中,100 次投擲的正面數量在 35 到 65 之間。事實上,大部分的重複産生 45 到 55 個正面數量。
理論上,正面數量可能在 0 到 100 之間,但模拟顯示可能值的範圍要小得多。
這是一個更普遍現象的例子,關于擲硬币中的變化,我們将在後面看到。
Monty Hall 問題
多年來這個問題已經使許多人感到困惑,包括數學家在内。 讓我們看看我們是否可以解決。
這個設定來源于一個名為“讓我們做個交易”(Let’s Make a Deal)的電視遊戲節目。Monty Hall 在二十世紀六十年代主持了這個節目,從此産生了一些副産品。 這個節目令人興奮的一部分是,雖然參賽者有機會赢得大獎,但他們可能最終會選擇不那麼理想的“zonks”。 這就是現在所謂的 Monty Hall 問題的基礎。
這個設定是一個遊戲節目,參賽者面對三個閉着的門。 在其中一扇門的後面是一輛奇特的汽車,另外兩扇門後面有一隻山羊。 參賽者不知道汽車的位置,必須按照以下規則進行嘗試。
- 參賽者進行初步選擇,但不打開那個門。
- 其他兩個門中至少有一個門的後面必須有一隻山羊。Monty 打開這些門之一來展示山羊, 維基百科 中顯示了他所有的榮耀。
- 還剩下兩個門,其中一個是參賽者的原始選擇。 其中一扇門後面有車,另一扇有一隻山羊。 參賽者現在可以選擇打開兩扇門中的哪一扇。
參賽者需要作出決定。 如果她想要這輛車,她應該選擇打開哪扇門? 她應該堅持最初的選擇,還是轉向另一個門? 這是 Monty Hall 問題。
解法
在涉及幾率的任何問題中,重要的随機性的假設。 假設有三分之一的幾率,參賽者的最初選擇是後面有車的門,這是合理的。
在這個假設下,解決這個問題的方法非常簡單,盡管簡單的解決方案并不能說服每個人。 無論如何就是這樣。
- 汽車在原來選擇的門後面的幾率是 1/3。
- 汽車在原來選擇的門後面或者剩餘的門後面。 它不能在其他地方。
- 是以,汽車在剩餘的門後的幾率是 2/3。
- 是以,選手應該更改選擇。
- 就是這樣,故事結束了。
不相信? 那麼讓我們模拟遊戲,看看結果如何。
模拟
我們開始建立兩個實用的數組,
doors
goats
,這會讓我們區分三個門和兩隻山羊。
doors = make_array('Car', 'Goat 1', 'Goat 2')
goats = make_array('Goat 1', 'Goat 2') 現在我們定義一個函數
monty_hall
來模拟遊戲,并按照這個順序傳回含有三個字元串的數組:
- 參賽選手的原始選擇的什麼
- Monty 排除了什麼
- 剩下的門是什麼
如果選手的原始選擇是帶山羊的門,蒙蒂必須扔掉另一隻山羊,剩下的就是這輛車。 如果最初的選擇是帶車的門,蒙蒂必須扔掉兩隻山羊中的一隻,剩下的就是另一隻羊。
是以很顯然,在前一節中定義的函數将是有用的。 它需要一個字元串和一個兩個元素的數組; 如果字元串等于其中一個元素,則傳回另一個元素。
def other_one(x, a_b):
if x == a_b.item(0):
return a_b.item(1)
elif x == a_b.item(1):
return a_b.item(0)
else:
return 'Input Not Valid' 如果選手的原始選擇是山羊,遊戲的結果是這二者之一:
original = 'Goat 1'
make_array(original, other_one(original, goats), 'Car')
array(['Goat 1', 'Goat 2', 'Car'],
dtype='<U6')
original = 'Goat 2'
make_array(original, other_one(original, goats), 'Car')
array(['Goat 2', 'Goat 1', 'Car'],
dtype='<U6') 現在我們可以把所有這些代碼放到
monty_hall
函數中,來模拟一次遊戲的結果。 該函數不帶任何參數。
參賽者的原始選擇将是三門之中随機選擇的門。
為了檢查原始選擇是否是山羊,我們首先寫一個名為
is_goat
的小函數:
def is_goat(door_name):
""" Check whether the name of a door (a string) is a Goat.
Examples:
=========
>>> is_goat('Goat 1')
True
>>> is_goat('Goat 2')
True
>>> is_goat('Car')
False
"""
if door_name == "Goat 1":
return True
elif door_name == "Goat 2":
return True
else:
return False
def monty_hall():
""" Play the Monty Hall game once
and return an array of three strings:
original choice, what Monty throws out, what remains
"""
original = np.random.choice(doors)
if is_goat(original):
return make_array(original, other_one(original, goats), 'Car')
else:
throw_out = np.random.choice(goats)
return make_array(original, throw_out, other_one(throw_out, goats)) 讓我們玩幾次這個遊戲。這裡是一個結果。你應該運作幾次單元格來觀察結果如何變化。
monty_hall()
array(['Car', 'Goat 2', 'Goat 1'],
dtype='<U6') 為了衡量不同結果發生的頻率,我們必須玩多次遊戲并收集結果。 為此,我們将使用
for
循環。
我們将首先定義三個空數組,每個數組對應原始選擇,Monty 排除了什麼,剩下的是什麼。然後我們将玩這個遊戲 N 次并收集結果。我們已經将 N 設為 10,000,但是你可以改變它。
# Number of times we'll play the game
N = 10000
original = make_array() # original choice
throw_out = make_array() # what Monty throws out
remains = make_array() # what remains
for i in np.arange(N):
result = monty_hall() # the result of one game
# Collect the results in the appropriate arrays
original = np.append(original, result.item(0))
throw_out = np.append(throw_out, result.item(1))
remains = np.append(remains, result.item(2))
# The for-loop is done! Now put all the arrays together in a table.
results = Table().with_columns(
'Original Door Choice', original,
'Monty Throws Out', throw_out,
'Remaining Door', remains
)
results | Original Door Choice | Monty Throws Out | Remaining Door |
|---|---|---|
| Car | Goat 1 | Goat 2 |
為了看看選手是否應該堅持原來的選擇或更改,讓我們看看她的兩個選項後面的車的頻率。
results.group('Original Door Choice') | count | |
|---|---|
| 3312 | |
| 3382 | |
| 3306 |
results.group('Remaining Door') | 6688 | |
| 1640 | |
| 1672 |
我們的解決方案說明了,這輛車有三分之二的幾率在剩下的門後面,這是相當不錯的近似值。 如果參賽者更改了她的選擇,她有兩倍的可能性會得到車。
為了使結果可視化,我們可以将上面的兩個表格連接配接在一起并繪制疊加的條形圖。
results_o = results.group('Original Door Choice')
results_r = results.group('Remaining Door')
joined = results_o.join('Original Door Choice', results_r, 'Remaining Door')
combined = joined.relabeled(0, 'Item').relabeled(1, 'Original Door').relabeled(2, 'Remaining Door')
combined | Item | Original Door | |
|---|---|---|
combined.barh(0) 注意三條藍色條形幾乎相等 - 原始選擇有同等可能是三個可用條目中的任何一條。 但是,汽車對應的金色條形是藍色條形的兩倍。
模拟證明了,如果參賽者改變選擇,她有兩倍的可能性獲勝。
發現機率
幾個世紀以來,對于什麼是機率存在哲學争論。有些人認為機率是相對頻率;其他人認為他們是長期的相對頻率較長;還有一些人認為機率是個人不确定性程度的主觀測量。
在這個課程中,大多數機率将是相對頻率,盡管許多人會有主觀的解釋。無論如何,在不同的解釋中,機率計算群組合的方式是一緻的。
按照慣例,機率是介于 0 和 1 之間的數字,或者 0% 和 100% 之間。不可能的事件機率為 0。确定的事件機率為 1。
數學是準确發現機率的主要工具,盡管計算機也可用于此目的。模拟可以提供出色的近似,具有很高的機率。在本節中,我們将以非正式方式制定一些簡單的規則來管理機率的計算。在随後的章節中,我們将回到模拟來近似複雜事件的機率。
我們将使用标準符号
來表示“事件”發生的機率,我們将交替使用“幾率”和“機率”兩個字。
事件不會發生的時候
如果事件發生的機率是 40%,不發生的幾率就是 60%。這個自然的計算可以這樣秒速:
所有結果等可能的時候
如果你投擲一個普通的骰子,一個自然的假設是,所有六個面都是等可能的。 那麼一個面出現的機率可以很容易地計算出來。 例如,骰子顯示偶數的幾率是:
與之相似:
通常:
前提是所有的結果都是等可能的。
并非所有的随機現象都像骰子一樣簡單。 下面的兩個主要的機率規則甚至允許數學家在複雜的情況下找到機率。
兩個事件必須同時發生時
假設你有一個盒子,包含三張紙條:一張紅色,一張藍色和一張綠色。 假設你随機抽兩張紙條而不放回;也就是你把三張紙條打亂,抽一張,打亂其餘兩張,再從這兩張中抽出一張。 你先得到綠色紙條,然後是紅色紙條的幾率是多少?
有六種可能的顔色對:RB,BR,RG,GR,BG,GB(我們已經縮寫了每種顔色的名字,就是它的第一個字母)。 所有這些都是抽樣方案是等可能的,隻有其中一個(GR)使事件發生。是以:
但是還有另外一種方法來得到答案,可以用兩個階段來思考這個事件。 必須首先抽取綠色紙條。幾率是 1/3,也就是說在所有實驗的大約 1/3 的重複中,先抽取了綠色紙條,但事件還沒完成。在這 1/3 的重複中,必須再次抽取紅色紙條。這個發生在大約 1/2 的重複中,是以:
這個計算通常按照事件順序,像這樣:
因數 1/2 叫做“假設第一次出現了綠色紙條,第二次出現紅色紙條的條件幾率”。
通常,我們擁有乘法規則:
兩個事件同時發生的機率,等于第一個事件發生的機率,乘上第一個事件發生的情況下第二個事件發生的機率。
是以,這裡有兩個條件 - 一個事件必須發生,另一個也是 - 幾率是分數的分數,這比兩個因數的任何一個都要小。 滿足的條件越多,滿足的可能性就越小。
事件以兩種不同的方式發生
相反,假設我們希望兩張紙條中的一張是綠色的,另一張是紅色的。 此事件不指定顔色必須出現的順序。是以他們可以以任何順序出現。
解決這樣的問題的一個好方法就是對事件進行劃分,以便它正好能夠以幾種不同的方式之一發生。 “一綠一紅”的自然劃分是:GR,RG。
根據上面的計算,GR 和 RG 每個的幾率都是 1/6。是以你可以通過把它們相加來計算一綠一紅的機率。
通常,我們擁有加法規則:
事件發生的機率,等于以第一種方式發生的機率,加上以第二種方式發生的機率。
隻要事件正好以兩種方式之一發生。
是以,當事件以兩種不同的方式之一發生時,發生的幾率是一些幾率的總和,是以比任何一種方式的幾率都大。
乘法規則可以自然擴充到兩個以上的事件,我們将在下面看到。 是以這個加法規則也有自然的擴充,事件可以以幾種不同的方式之一發生。
我們将所有這些規則組合成示例,并用示例來結束該部分。
至少有一個成功
資料科學家經常使用來自人群的随機樣本。 有時候問題就來了,就是人群中的一個特定個體選進樣本的可能性。為了找出幾率,這個人被稱為“成功”,問題是要找到樣本包含成功的幾率。
要看看如何計算這樣的幾率,我們從一個更簡單的設定開始:投擲硬币兩次。
如果你投擲硬币兩次,有四個等可能的結果:HH,HT,TH 和 TT。 我們把正面縮寫為 H ,反面縮寫為 T。至少有一個正面的幾率是 3/4。
得出這個答案的另一種方法是,弄清楚如果你不能得到至少一個正面,會發生什麼事情:這兩次投擲都必須是反面。是以:
要注意根據乘法規則:
這兩個觀察使我們能夠在任何給定數量的投擲中找到至少一個正面的幾率。 例如:
而現在我們有能力找到在骰子的投擲中,六點至少出現一次的幾率:
下表展示了,這些機率随着投擲數量從 1 增加到 50 而增加。
rolls = np.arange(1, 51, 1)
results = Table().with_columns(
'Rolls', rolls,
'Chance of at least one 6', 1 - (5/6)**rolls
)
results | Rolls | Chance of at least one 6 |
|---|---|
| 0.166667 | |
| 0.305556 | |
| 0.421296 | |
| 0.517747 | |
| 0.598122 | |
| 0.665102 | |
| 0.720918 | |
| 0.767432 | |
| 0.806193 | |
| 0.838494 |
(省略了 40 行)
随着投擲數量的增加,六點至少出現一次的幾率迅速增加。
results.scatter('Rolls') 在 50 次投擲中,你幾乎肯定能得到至少一個六。
results.where('Rolls', are.equal_to(50)) | 0.99989 |
像這樣的計算可以用來找到,随機樣本中選擇特定個體的幾率。 準确的計算将取決于抽樣方案。 但是我們上面的觀察的通常可以被推廣:增加随機樣本的大小增加了選擇個體的幾率。
抽樣
現在我們來仔細看看抽樣,例子基于
top_movies.csv
資料集。
top1 = Table.read_table('top_movies.csv')
top2 = top1.with_column('Row Index', np.arange(top1.num_rows))
top = top2.move_to_start('Row Index')
top.set_format(make_array(3, 4), NumberFormatter) | Row Index | Title | Studio | Gross | Gross (Adjusted) | Year |
|---|---|---|---|---|---|
| Star Wars: The Force Awakens | Buena Vista (Disney) | 906,723,418 | 906,723,400 | 2015 | |
| Avatar | Fox | 760,507,625 | 846,120,800 | 2009 | |
| Titanic | Paramount | 658,672,302 | 1,178,627,900 | 1997 | |
| Jurassic World | Universal | 652,270,625 | 687,728,000 | ||
| Marvel’s The Avengers | 623,357,910 | 668,866,600 | 2012 | ||
| The Dark Knight | Warner Bros. | 534,858,444 | 647,761,600 | 2008 | |
| Star Wars: Episode I - The Phantom Menace | 474,544,677 | 785,715,000 | 1999 | ||
| Star Wars | 460,998,007 | 1,549,640,500 | 1977 | ||
| Avengers: Age of Ultron | 459,005,868 | 465,684,200 | |||
| The Dark Knight Rises | 448,139,099 | 500,961,700 |
(省略了 190 行)
對表格的行進行抽樣
資料表的每一行代表一個個體;最重要的是,每個個體都是一部電影。 是以可以通過表格的行的抽樣來實作對個體的抽樣。
一行的内容是在同一個個體上測量的不同變量的值。 是以,行的内容的抽樣形成了每個變量值的樣本。
确定性樣本
當你隻是簡單地指定,你要選擇的集合中的哪些元素時,就不會涉及任何幾率,可以建立确定性樣本。
你已經做了很多次了,例如使用
take
:
top.take(make_array(3, 18, 100)) | 18 | Spider-Man | Sony | 403,706,375 | 604,517,300 | 2002 |
| 100 | Gone with the Wind | MGM | 198,676,459 | 1,757,788,200 | 1939 |
你也使用了
where
top.where('Title', are.containing('Harry Potter')) | 22 | Harry Potter and the Deathly Hallows Part 2 | 381,011,219 | 417,512,200 | 2011 | |
| 43 | Harry Potter and the Sorcerer’s Stone | 317,575,550 | 486,442,900 | 2001 | |
| Harry Potter and the Half-Blood Prince | 301,959,197 | 352,098,800 | |||
| Harry Potter and the Order of the Phoenix | 292,004,738 | 369,250,200 | 2007 | ||
| 62 | Harry Potter and the Goblet of Fire | 290,013,036 | 393,024,800 | 2005 | |
| 69 | Harry Potter and the Chamber of Secrets | 261,988,482 | 390,768,100 | ||
| 76 | Harry Potter and the Prisoner of Azkaban | 249,541,069 | 349,598,600 | 2004 |
雖然這些是電影的樣本,它們并不涉及幾率。
機率抽樣
很多資料科學都根據随機樣本中的資料得到結論。 根據随機樣本的正确解釋分析,需要資料科學家準确地檢查随機樣本。
總體是從中抽取樣本的所有元素的集合。
機率樣本是一種樣本,在抽取樣本之前,可以計算出的元素的任何子集将進入樣本的幾率。
在機率樣本中,所有的元素不需要有相同的選中幾率。
随機抽樣方案
例如,假設根據以下方案,從三個個體 A,B 和 C 組成的總體中選擇兩個個體:
- 個體 A 選中機率為 1。
- 個體 B 或 C 根據擲硬币來選擇:如果硬币為正面,選擇 B,否則,選擇 C。
這是一個大小為 2 的機率樣本。下面是所有非空子集的選中幾率:
A: 1
B: 1/2
C: 1/2
AB: 1/2
AC: 1/2
BC: 0
ABC: 0 個體 A 比 B 或 C 有更高的選中幾率;的确,個體 A 肯定會被選中。由于這些差異是已知的和量化的,是以在處理樣本時可以考慮這些差異。
系統樣本
想象一下,總體的所有元素都列出在序列中。 抽樣的一種方法是,先從清單中選擇一個随機的位置,然後是它後面的等間隔的位置。樣本由這些位置上的元素組成。這樣的樣本被稱為系統樣本。
在這裡,我們将選擇頂部一些行的系統樣本。我們最開始随機選取前 10 行中的一行,然後我們将選取它後面的每個第 10 行。
"""Choose a random start among rows 0 through 9;
then take every 10th row."""
start = np.random.choice(np.arange(10))
top.take(np.arange(start, top.num_rows, 10)) | 16 | Iron Man 3 | 409,013,994 | 424,632,700 | 2013 | |
| 26 | Spider-Man 2 | 373,585,825 | 523,381,100 | ||
| 36 | Minions | 336,045,770 | 354,213,900 | ||
| Iron Man 2 | 312,433,331 | 341,908,200 | 2010 | ||
| 56 | The Twilight Saga: New Moon | Sum. | 296,623,634 | 338,517,700 | |
| 66 | Meet the Fockers | 279,261,160 | 384,305,300 | ||
| 86 | The Exorcist | 232,906,145 | 962,212,800 | 1973 | |
| 96 | Back to the Future | 210,609,762 | 513,740,700 | 1985 |
(省略了 10 行)
運作單元個幾次,看看輸出如何變化。
這個系統樣本是一個機率樣本。 在這個方案中,所有的行都有機會被選中。 例如,當且僅當第 3 行被選中時,第 23 行才被選中,并且其幾率是 1/10。
但并不是所有的子集都有相同的選中幾率。 由于選中的行是等間隔的,大多數行的子集都沒有機會被選中。 唯一可能的子集是由所有間隔為 10 的行構成的子集。任何這些子集都以 1/10 的幾率被選中。 其他子集,如包含表格前 11 行的子集,選中幾率都是 0。
放回或不放回的随機抽樣
在這個課程中,我們将主要處理兩個最直接的抽樣方法。
首先是帶放回的随機抽樣,它(如我們前面所見)是
np.random.choice
從數組中抽樣時的預設行為。
另一個稱為“簡單随機樣本”,是随機抽取的樣本,不帶放回。在下一個個體被抽中之前,抽中的個體不會放回總體。例如,當你發牌時,就會發生這種抽樣。
在下一章中,我們将使用模拟來研究帶放回和不放回的大樣本随機抽取。
繪制随機樣本需要謹慎和精确。這不是随便的,即使這是“随機”一詞的口語意義。如果你站在街頭,選取前十名經過的人作為樣本,你可能會認為你在随機抽樣,因為你沒有選擇誰走過。但它不是一個随機樣本 - 這是一個友善的例子。你沒有提前知道每個人進入樣本的機率,也許甚至你沒有具體指定誰在總體中。