Python3 執行個體
對一個有向無環圖(Directed Acyclic Graph簡稱DAG)G進行拓撲排序,是将G中所有頂點排成一個線性序列,使得圖中任意一對頂點u和v,若邊(u,v)∈E(G),則u線上性序列中出現在v之前。通常,這樣的線性序列稱為滿足拓撲次序(Topological Order)的序列,簡稱拓撲序列。簡單的說,由某個集合上的一個偏序得到該集合上的一個全序,這個操作稱之為拓撲排序。
在圖論中,由一個有向無環圖的頂點組成的序列,當且僅當滿足下列條件時,稱為該圖的一個拓撲排序(英語:Topological sorting):
- 每個頂點出現且隻出現一次;
- 若A在序列中排在B的前面,則在圖中不存在從B到A的路徑。
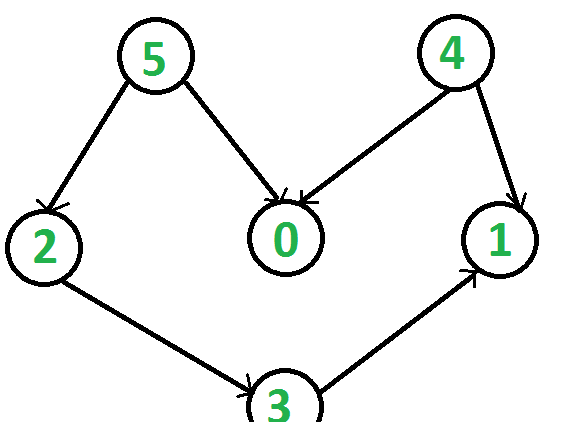
執行個體
from collections import defaultdict
class Graph:
def __init__(self,vertices):
self.graph = defaultdict(list)
self.V = vertices
def addEdge(self,u,v):
self.graph[u].append(v)
def topologicalSortUtil(self,v,visited,stack):
visited[v] = True
for i in self.graph[v]:
if visited[i] == False:
self.topologicalSortUtil(i,visited,stack)
stack.insert(0,v)
def topologicalSort(self):
visited = [False]*self.V
stack =[]
for i in range(self.V):
print (stack)
g= Graph(6)
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
print ("拓撲排序結果:")
g.topologicalSort()
執行以上代碼輸出結果為:
拓撲排序結果:
[5, 4, 2, 3, 1, 0]