題目描述
給定一個整數數組和一個整數 k,你需要找到該數組中和為 k 的連續的子數組的個數。
示例 1 :
輸入:nums = [1,1,1], k = 2
輸出: 2 , [1,1] 與 [1,1] 為兩種不同的情況。
說明 :
數組的長度為 [1, 20,000]。
數組中元素的範圍是 [-1000, 1000] ,且整數 k 的範圍是 [-1e7, 1e7]。
思路分析
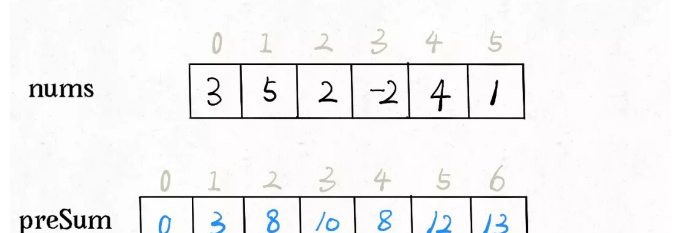
這個字首和數組preSum的含義也很好了解,preSum[i]就是nums[0..i-1]的和。那麼如果我們想求nums[i..j]的和,隻需要一步操作preSum[j+1]-preSum[i]即可,而不需要重新去周遊數組了。
int subarraySum(int[] nums, int k) {
int n = nums.length;
// 構造字首和
int[] sum = new int[n + 1];
sum[0] = 0;
for (int i = 0; i < n; i++)
sum[i + 1] = sum[i] + nums[i];
int ans = 0;
// 窮舉所有子數組
for (int i = 1; i <= n; i++)
for (int j = 0; j < i; j++)
// sum of nums[j..i-1]
if (sum[i] - sum[j] == k)
ans++;
return ans;
} 這個解法的時間複雜度
空間複雜度
,并不是最優的解法。不過通過這個解法了解了字首和數組的工作原理之後,可以使用一些巧妙的辦法把時間複雜度進一步降低。
優化的思路是:我直接記錄下有幾個sum[j]和sum[i]-k相等,直接更新結果,就避免了内層的 for 循環。我們可以用哈希表,在記錄字首和的同時記錄該字首和出現的次數。
代碼實作
public int subarraySum(int[] nums, int k) {
Map<Integer,Integer> map = new HashMap();
int sum_i = 0;
int sum_j = 0;
int result = 0;
map.put(0,1);
for(int i=0;i<nums.length;i++){
sum_i = sum_i + nums[i];
//和目前字首和sum_i差k的字首和為sum_j
sum_j = sum_i- k;
if(map.get(sum_j)!=null){
//之前存在這個字首和就把結果加1
result = result + map.get(sum_j);
}
map.put(sum_i,map.getOrDefault(sum_i,0)+1);
}
return result;
}