知識圖譜聽起來很高大上,而且也應用廣泛,如用于血緣關系查詢,知識鍊展示,異動分析。而圖資料庫,你可以到網上搜搜,基本就是像 neo4j, janusgraph, HugeGraph,還有像阿裡閉源提供的graphcompute服務...
如果有個圖譜類似的需求,你會怎麼辦呢?一來就上真的圖譜真的好嗎?也許前期就三兩個關系鍊,也許隻是業務試水,你就去搞個真的圖資料庫過來?是不是太浪費了,因為業務如果發現不成可能立即改變方向了,而你卻為前期工作和裝置買單。
是以,實際上前期我們最好自己實作一些簡單的關系鍊維護即可。而其中的查詢實作,則隻需要自己根據關系,做每個原子查詢實作即可。
那麼,為了能夠适應稍微的關系變化,也許我們還是需要效仿下圖資料庫的概念。那麼,現在的第一個問題就是:如何使用文字表述一個圖關系鍊?
1. 如何定義規範?
圖資料庫三大要素: 實體, 關系, 客體 。
實際上要解決這個問題倒也不難,隻要自己定一種表示方法,自己能看懂就行,不去管其他人。比如用 '1,2,3' 代表先1後2再3... 但實際上,想要表示稍微複雜點的結構,也許并不是特别容易呢。而且,如果想要考慮後續可能的切真正的圖資料庫,為何不參考下别人的标準呢?雖然沒有統一的标準,但無疑任何一家标準都會比自行定義要好要完善要考慮得更多。
比如現在通用些的,cypher, gremlin... 可以說都是一些規範性質的東西,但目前圖資料庫查詢方面并沒有類似于sql92一樣的标準,将大家限制到一條統一戰線上。是以,我們如果也隻能選擇一家站隊,大家可以網上搜尋下資料,參考下來,好像cypher更形象化些,尤其是各種箭頭的使用比較友善。而gremlin則是使用一系列的單詞,通過鍊式程式設計的方式進行展示,無法評論好壞,這隻能交給時間。标準化真的是一個好東西!
cypher中比如要表示A與的B的關系可以是: (:A)-[:關系]->(:B)
而對于多個複雜關系,則可以用多個類似的關系關聯起來就可以了。
嗯,看起來不錯。表示的方式定好了,那麼我們如何具體處理關系呢?
2. 如何表示一個現實的圖關系?
如下圖所示,我們有如下關系,應該如何定義字元表達方法,以達到配置的目的?(如果能夠處理好如下圖關系,更複雜的關系又何嘗不是手到擒來?)
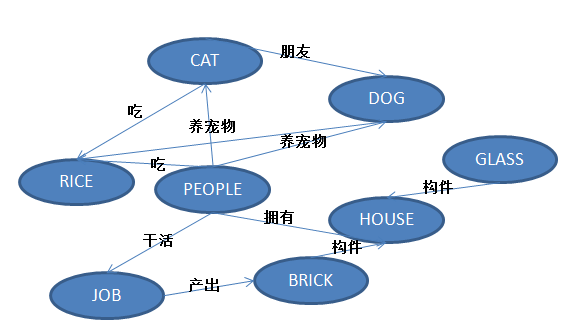
按照第1節中我們定義的規範,我們可以用如下字元串表示。
(:PEOPLE)-[:養寵物]->(:CAT)-[:吃]->(:RICE)
,(:PEOPLE)-[:吃]->(:RICE)
,(:PEOPLE)-[:養寵物]->(:DOG)
,(:PEOPLE)-[:擁有]->(:HOUSE)
,(:PEOPLE)-[:幹活]->(:JOB)
,(:CAT)-[:朋友]->(:DOG)
,(:DOG)-[:吃]->(:RICE)
,(:JOB)-[:産出]->(:BRICK)
,(:HOUSE)<-[:構件]-(:BRICK)
,(:HOUSE)<-[:構件]-(:GLASS) 應該說還是比較直覺的,基本上我們隻要按照圖所示的關系,描述出出入邊和關系就可以了。而且還有相應的cypher官方規範支援,也不用寫文檔,大家就可以很友善的接受了。
3. 如何解析圖關系?
如上,我們已經用字元串表示出了關系了。但單是字元串,是并不能被應用了解的。我們需要解析為具體的資料結構,然後才可以根據關系推導出具體的血緣依賴。這是本文的重點。
實際也不複雜,我們僅僅使用到了cypher中非常少的幾個元素表示法,是以也僅需解析出該幾個字元,然後在記憶體中建構出相應的關系即可。
具體代碼實作如下:
3.1. 解析架構
所謂架構就是整體流程管控代碼,它會讓你明白整個系統是如何work的。
import com.my.mvc.app.common.helper.graph.GraphNodeEntityTree;
import com.my.mvc.app.common.helper.graph.NodeDiscoveryDirection;
import com.my.mvc.app.common.helper.graph.VertexEdgeSchemaDescriptor;
import com.my.mvc.app.common.helper.graph.VertexOrEdgeType;
import com.my.mvc.app.common.util.CommonUtil;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
/**
* 功能描述: 簡單圖文法解析器(類 cypher 文法)
*
* 請參考網上 cypher 資料
*
*/
public class SimpleGraphSchemaSyntaxParser {
/**
* 解析配置圖譜關系配置為樹結構
*
* @param cypherGraphSchema 類cypher文法的 關系表示語句
* @return 解析好的樹結構
*/
public static GraphNodeEntityTree parseGraphSchemaAsTree(String cypherGraphSchema) {
List<VertexEdgeSchemaDescriptor> flatNodeList = tokenize(cypherGraphSchema);
return buildGraphAstTree(flatNodeList);
}
/**
* 建構圖關系抽象文法樹
*
* @param flatNodeList 平展的圖節點清單
* @return 建構好的執行個體
*/
private static GraphNodeEntityTree buildGraphAstTree(
List<VertexEdgeSchemaDescriptor> flatNodeList) {
Map<String, GraphNodeEntityTree>
uniqVertexContainer = new HashMap<>();
GraphNodeEntityTree root = new GraphNodeEntityTree(flatNodeList.get(0));
uniqVertexContainer.put(flatNodeList.get(0).getVertexLabelType(), root);
GraphNodeEntityTree parent;
GraphNodeEntityTree afterNode;
for ( int i = 1; i < flatNodeList.size(); i++ ) {
VertexEdgeSchemaDescriptor vertexOrEdge1 = flatNodeList.get(i);
if(vertexOrEdge1.getNodeType() == VertexOrEdgeType.EDGE) {
// 整體關系建構以邊為依據,關聯前後兩個點,todo: 每個頂點都應該被添加到頂點清單中。以便後續可查
VertexEdgeSchemaDescriptor vertexPrev = flatNodeList.get(i - 1);
if(vertexPrev.getNodeType() != VertexOrEdgeType.VERTEX) {
continue;
}
if(++i >= flatNodeList.size()) {
throw new RuntimeException("圖譜文法錯誤:缺少客體關系配置, near 邊["
+ vertexOrEdge1.getRawWord() + "]");
}
VertexEdgeSchemaDescriptor relation = vertexOrEdge1;
VertexEdgeSchemaDescriptor vertexAfter = flatNodeList.get(i);
parent = uniqVertexContainer.get(vertexPrev.getVertexLabelType());
afterNode = uniqVertexContainer.get(vertexAfter.getVertexLabelType());
if(parent == null) {
parent = root;
uniqVertexContainer.putIfAbsent(vertexPrev.getVertexLabelType(),
parent);
}
if(afterNode == null) {
afterNode = new GraphNodeEntityTree(vertexAfter);
uniqVertexContainer.put(vertexAfter.getVertexLabelType(), afterNode);
}
if(relation.getDirection() == NodeDiscoveryDirection.OUT) {
parent.addOutVertex(afterNode, relation);
}
else {
parent.addInVertex(afterNode, relation);
}
} // todo: 請嘗試添加頂點到uniqContainer中
if(vertexOrEdge1.getNodeType() == VertexOrEdgeType.VERTEX) {
uniqVertexContainer.putIfAbsent(new GraphNodeEntityTree(vertexOrEdge1));
}
}
root.setUniqVertexTypes(uniqVertexContainer);
return root;
}
/**
* 拆分圖關系schema為 可了解的邊和點
*
* @param cypherGraphSchema 建關系語句,如 (:A)-[:被引用]->(:B)
* @return 拆解後的token清單
*/
private static List<VertexEdgeSchemaDescriptor> tokenize(String cypherGraphSchema) {
String[] relationArr = cypherGraphSchema.split(",");
List<VertexEdgeSchemaDescriptor> flatNodeList = new ArrayList<>();
for (String relation1 : relationArr) {
char[] src = relation1.trim().toCharArray();
for (int i = 0; i < src.length; i++) {
char ch = src[i];
// 頂點
if(ch == '(') {
StringBuilder specNameBuilder = new StringBuilder();
while (i + 1 < src.length) {
char nextCh = src[i + 1];
if(nextCh == ':') {
String vertexLabel = CommonUtil.readSplitWord(
src, i, ':', ')', false);
flatNodeList.add(VertexEdgeSchemaDescriptor.newVertex(
specNameBuilder.toString() + ":" + vertexLabel,
vertexLabel));
i += vertexLabel.length() + 2;
break;
}
specNameBuilder.append(nextCh);
++i;
}
continue;
}
// 出射邊關系, (:SRC)-[:RELATION]->(:DST)
if(ch == '-' &&
i + 1 < src.length && src[i + 1] == '[') {
++i;
StringBuilder specNameBuilder = new StringBuilder();
while (i + 1 < src.length) {
char nextCh = src[i + 1];
if(nextCh == ':') {
String edgeLabel = CommonUtil.readSplitWord(
src, i, ':', ']', false);
int nextVertexStart = i + edgeLabel.length() + 2;
if(nextVertexStart + 2 >= src.length) {
throw new RuntimeException("圖譜文法錯誤: 缺少客體" +
", near '" + new String(src, nextVertexStart,
src.length - nextVertexStart));
}
if(src[++nextVertexStart] != '-'
|| src[++nextVertexStart] != '>') {
throw new RuntimeException("圖譜文法錯誤: 主體後面需緊跟關系 ->" +
", near '" + new String(src, nextVertexStart,
src.length - nextVertexStart));
}
flatNodeList.add(VertexEdgeSchemaDescriptor.newEdge(
specNameBuilder.toString() + ":" + edgeLabel,
edgeLabel, NodeDiscoveryDirection.OUT));
i = nextVertexStart;
break;
}
specNameBuilder.append(nextCh);
++i;
}
continue;
}
// 入射邊關系, (:SRC)<-[:RELATION]-(:DST)
if(ch == '<') {
if(i + 2 > src.length) {
throw new RuntimeException("圖譜文法錯誤: 長度不比對, near '"
+ new String(src, i, src.length - i));
}
if(src[++i] != '-' || src[++i] != '[') {
throw new RuntimeException("圖譜文法錯誤: 邊關系配置錯誤, near '"
+ new String(src, i, src.length - i));
}
StringBuilder specNameBuilder = new StringBuilder();
while (i + 1 < src.length) {
char nextCh = src[i + 1];
if(nextCh == ':') {
String edgeLabel = CommonUtil.readSplitWord(
src, i, ':', ']', false);
int nextVertexStart = i + edgeLabel.length() + 2;
if(nextVertexStart + 2 >= src.length) {
throw new RuntimeException("圖譜文法錯誤: 缺少客體" +
", near '" + new String(src, nextVertexStart,
src.length - nextVertexStart));
}
if(src[++nextVertexStart] != '-'
|| src[nextVertexStart + 1] != '(') {
throw new RuntimeException("圖譜文法錯誤: 主體後面需緊跟關系 -> " +
", near '" + new String(src, nextVertexStart,
src.length - nextVertexStart));
}
flatNodeList.add(VertexEdgeSchemaDescriptor.newEdge(
specNameBuilder.toString() + ":" + edgeLabel,
edgeLabel, NodeDiscoveryDirection.IN));
i = nextVertexStart;
break;
}
specNameBuilder.append(nextCh);
++i;
}
}
}
}
return flatNodeList;
}
} 怎麼樣,不複雜吧。就是兩個步驟:1. 解析每個單個元素資訊; 2. 根據單元素資訊,建構出上下級關系;
使用 IN 代表入方向關系,用 OUT 代表出方向關系,每兩個頂點之間都有一條邊相連。大體就是這樣了。但是明顯,還有許多細節需要我們去考慮,比如邊關系放在哪裡?如何添加相關節點?這些東西是需要特定的資料結構支援的。看我細細道來:
3.2. 單節點數結構
所謂單節點,即是一個頂點的描述。當我們站在任意關系點上來看整體圖的結構,如果整個圖是連通的,那麼理論上,通過這個節點可以探索到任意其他節點。是以,其實它的定義非常重要。
package com.my.mvc.app.common.helper.graph;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
/**
* 功能描述: 簡單圖結構樹描述類
*
*/
public class GraphNodeEntityTree {
/**
* 目前頂點描述
*/
private VertexEdgeSchemaDescriptor vertex;
/**
* 關系邊容器
*/
private Map<NodeDiscoveryDirection, List<RelationWithVertexDescriptor>>
relations = new HashMap<>();
/**
* 入射方向節點
*/
private List<GraphNodeEntityTree> in = new ArrayList<>();
/**
* 出射方向節點
*/
private List<GraphNodeEntityTree> out = new ArrayList<>();
/**
* 所有頂點執行個體容器
*/
private Map<String, GraphNodeEntityTree> uniqVertexTypes;
public GraphNodeEntityTree(VertexEdgeSchemaDescriptor vertex) {
this.vertex = vertex;
uniqVertexTypes = new HashMap<>();
}
public void setUniqVertexTypes(Map<String, GraphNodeEntityTree> uniqVertexTypes) {
this.uniqVertexTypes = uniqVertexTypes;
}
public void addRelation(VertexEdgeSchemaDescriptor srcEntity,
VertexEdgeSchemaDescriptor relation,
VertexEdgeSchemaDescriptor dstEntity) {
List<RelationWithVertexDescriptor> list = relations.computeIfAbsent(
relation.getDirection(), k -> new ArrayList<>());
list.add(new RelationWithVertexDescriptor(srcEntity, relation, dstEntity));
}
public GraphNodeEntityTree addInVertex(GraphNodeEntityTree embeddedEntity,
VertexEdgeSchemaDescriptor relation) {
embeddedEntity.addOutVertexInner(this, relation.reverseDirection());
addInVertexInner(embeddedEntity, relation);
return embeddedEntity;
}
private GraphNodeEntityTree addInVertexInner(GraphNodeEntityTree embeddedEntity,
VertexEdgeSchemaDescriptor relation) {
in.add(embeddedEntity);
addRelation(vertex, relation, embeddedEntity.getVertex());
return embeddedEntity;
}
public GraphNodeEntityTree addOutVertex(GraphNodeEntityTree embeddedEntity,
VertexEdgeSchemaDescriptor relation) {
embeddedEntity.addInVertexInner(this, relation.reverseDirection());
addOutVertexInner(embeddedEntity, relation);
return embeddedEntity;
}
private GraphNodeEntityTree addOutVertexInner(GraphNodeEntityTree embeddedEntity,
VertexEdgeSchemaDescriptor relation) {
out.add(embeddedEntity);
addRelation(this.getVertex(), relation, embeddedEntity.getVertex());
return embeddedEntity;
}
public VertexEdgeSchemaDescriptor getVertex() {
return vertex;
}
/**
* 擷取關系名稱
*
* @param nodeIndex 節點序号
* @param direction 方向
* @return 關系名稱描述
*/
public String getRelationName(int nodeIndex, NodeDiscoveryDirection direction) {
List<RelationWithVertexDescriptor> list = relations.get(direction);
if(list == null || list.isEmpty()) {
return null;
}
return list.get(nodeIndex).getRelationName();
}
public List<GraphNodeEntityTree> getIn() {
return in;
}
public List<GraphNodeEntityTree> getOut() {
return out;
}
/**
* 快速擷取圖節點根(根據頂點label)
*
* @param vertexLabel 頂點辨別
* @return 節點所在執行個體, 找不到對應節點則傳回 null
*/
public GraphNodeEntityTree getNodeEntityTreeByVertexLabel(
String vertexLabel) {
return uniqVertexTypes.get(vertexLabel);
}
} 可以說後續的操作入口都是在這裡的,是以重點關注。
3.3. 圖頂點和邊描述類
最開始有一個token化的過程,那麼token化之後,如何定義也比較重要,我們統一使用一個描述類來定義:
package com.my.mvc.app.common.helper.graph;
/**
* 功能描述: 圖頂點和邊描述類
*
*/
public class VertexEdgeSchemaDescriptor {
private String rawWord;
private VertexOrEdgeType nodeType;
private String vertexLabelType;
private String relationName;
private NodeDiscoveryDirection direction;
private VertexEdgeSchemaDescriptor(String rawWord,
VertexOrEdgeType nodeType,
String vertexLabelType,
String relationName,
NodeDiscoveryDirection direction) {
this.rawWord = rawWord;
this.nodeType = nodeType;
this.vertexLabelType = vertexLabelType;
this.relationName = relationName;
this.direction = direction;
}
/**
* 建立頂點執行個體
*
* @param rawWord 原始字元描述
* @param vertexLabelType 解析後的頂點類型(枚舉完成所有點類型)
* @return 頂點執行個體
*/
public static VertexEdgeSchemaDescriptor newVertex(String rawWord, String vertexLabelType) {
return new VertexEdgeSchemaDescriptor(rawWord, VertexOrEdgeType.VERTEX,
vertexLabelType, null, null);
}
/**
* 建立邊執行個體
*
* @param rawWord 原始字元描述
* @param relationName 關系名稱(當id使用)
* @param direction 關系方向( -> 出方向OUT, <- 入方向IN )
* @return 邊執行個體
*/
public static VertexEdgeSchemaDescriptor newEdge(String rawWord,
String relationName,
NodeDiscoveryDirection direction) {
return new VertexEdgeSchemaDescriptor(rawWord, VertexOrEdgeType.EDGE,
null, relationName, direction);
}
public String getRawWord() {
return rawWord;
}
public VertexOrEdgeType getNodeType() {
return nodeType;
}
public String getVertexLabelType() {
return vertexLabelType;
}
public String getRelationName() {
return relationName;
}
public NodeDiscoveryDirection getDirection() {
return direction;
}
public VertexEdgeSchemaDescriptor reverseDirection() {
return new VertexEdgeSchemaDescriptor(rawWord, nodeType,
vertexLabelType, "-" + relationName,
direction.reverse());
}
@Override
public String toString() {
// 點描述
if(nodeType == VertexOrEdgeType.VERTEX) {
return nodeType + "{" +
"rawWord='" + rawWord + '\'' +
", vertexLabelType=" + vertexLabelType +
'}';
}
// 邊描述
return nodeType + "{" +
"rawWord='" + rawWord + '\'' +
", relationName='" + relationName + '\'' +
", direction=" + direction +
'}';
}
} 主要就是原始字元串,定義邊、定義點。類似與單詞的聚合吧。
3.4. 節點關系描述
我們需要清楚地知道各個點與各個點間的關系,是以需要一個關系描述類,來展示這東西。(實際上核心并未使用該關系)
package com.my.mvc.app.common.helper.graph;
/**
* 功能描述: 關系執行個體, 實體 -> 關系 -> 客體
*
*/
public class RelationWithVertexDescriptor {
/**
* 源點、起點
*/
private final VertexEdgeSchemaDescriptor srcVertex;
/**
* 目标點
*/
private final VertexEdgeSchemaDescriptor dstVertex;
/**
* 關系(名稱)
*/
private final VertexEdgeSchemaDescriptor relation;
public RelationWithVertexDescriptor(VertexEdgeSchemaDescriptor srcVertex,
VertexEdgeSchemaDescriptor relation,
VertexEdgeSchemaDescriptor dstVertex) {
this.srcVertex = srcVertex;
this.dstVertex = dstVertex;
this.relation = relation;
}
public VertexEdgeSchemaDescriptor getSrcVertex() {
return srcVertex;
}
public VertexEdgeSchemaDescriptor getDstVertex() {
return dstVertex;
}
/**
* 擷取目前關系名稱
*/
public String getRelationName() {
return relation.getRelationName();
}
@Override
public String toString() {
if(relation.getDirection() == NodeDiscoveryDirection.OUT) {
return srcVertex.getRawWord() + "(" + srcVertex.getVertexLabelType() + ")" +
" -> " + relation.getRelationName() +
" -> " + dstVertex.getRawWord() + "(" + dstVertex.getVertexLabelType() + ")"
;
}
return srcVertex.getRawWord() + "(" + srcVertex.getVertexLabelType() + ")" +
" <- " + relation.getRelationName() +
" <- " + dstVertex.getRawWord() + "(" + dstVertex.getVertexLabelType() + ")"
;
}
} 雖實際用處不大,但是當你在debug的時候,這個描述類可以很友善地讓你觀察到解析是否正确。
3.5. 幾個基礎類型定義
1. 方向定義(實際上方向我們一定要有的概念就是,它永遠是相對的,如 A->B,對A來說是出方向,而對B來說則是入方向,此概念不清将會帶來大麻煩)
package com.my.mvc.app.common.helper.graph;
/**
* 功能描述: 探索方向定義
*
**/
public enum NodeDiscoveryDirection {
/**
* 入方向, 上遊
*/
IN,
/**
* 出方向, 下遊
*/
OUT,
;
public NodeDiscoveryDirection reverse() {
if(this == OUT) {
return IN;
}
return OUT;
}
} 2. 邊或點類型定義
package com.my.mvc.app.common.helper.graph;
/**
* 功能描述: 邊或點類型定義
*
*/
public enum VertexOrEdgeType {
VERTEX,
EDGE,
;
} 此類型雖然簡單,但卻會影響到後續整體抽象文法樹的建構。如此,整個解析子產品就完成了。你可以完整的将如上字元解析為實體關系了。
4. 單元測試
經過測試才算真正可用。
package com.my.test.common.parser;
import com.my.mvc.app.common.helper.SimpleGraphSchemaSyntaxParser;
import com.my.mvc.app.common.helper.graph.GraphNodeEntityTree;
import com.my.mvc.app.common.helper.graph.NodeDiscoveryDirection;
import org.junit.Test;
import java.util.List;
public class SimpleGraphSchemaSyntaxParserTest {
// 測試腳本
@Test
public void testParseGraphSchema() throws InterruptedException {
String graphSchema = "(:PEOPLE)-[:養寵物]->(:CAT)-[:吃]->(:RICE)\n"
+ ",(:PEOPLE)-[:吃]->(:RICE)\n"
+ ",(:PEOPLE)-[:養寵物]->(:DOG)\n"
+ ",(:PEOPLE)-[:擁有]->(:HOUSE)"
+ ",(:PEOPLE)-[:幹活]->(:JOB)"
+ ",(:CAT)-[:朋友]->(:DOG)"
+ ",(:DOG)-[:吃]->(:RICE)"
+ ",(:JOB)-[:産出]->(:BRICK)"
+ ",(:HOUSE)<-[:構件]-(:BRICK)"
+ ",(:HOUSE)<-[:構件]-(:GLASS)"
;
GraphNodeEntityTree tree = SimpleGraphSchemaSyntaxParser
.parseGraphSchemaAsTree(graphSchema);
String searchFromLabel = "PEOPLE";
NodeDiscoveryDirection direction = NodeDiscoveryDirection.OUT;
int maxDepth = 10;
System.out.println("->" + searchFromLabel + ", direction:" + direction + ", depth:" + maxDepth);
GraphNodeEntityTree searchRootFrom
= tree.getNodeEntityTreeByVertexLabel(searchFromLabel);
int allNodes = traversalNodesWithDirection(searchRootFrom,
direction, maxDepth, maxDepth);
System.out.println("allNodes: " + allNodes);
Thread.sleep(5);
}
/**
* 按某方向周遊所有節點
*
* @param root 搜尋起點
* @param direction 方向, IN, OUT
* @param maxDepth 搜尋最大深度
* @param remainSearchDepth 剩餘搜尋深度
* @return 所有節點數
*/
private static int traversalNodesWithDirection(GraphNodeEntityTree root,
NodeDiscoveryDirection direction,
int maxDepth,
int remainSearchDepth) {
if(remainSearchDepth <= 0) {
return 0;
}
List<GraphNodeEntityTree> subBranches;
if(direction == NodeDiscoveryDirection.OUT) {
subBranches = root.getOut();
}
else {
subBranches = root.getIn();
}
if(subBranches == null || subBranches.isEmpty()) {
return 0;
}
String whitespaceUnit = " ";
StringBuilder preWhitespaceBuilder = new StringBuilder(whitespaceUnit);
for (int i = 1; i < maxDepth - remainSearchDepth + 1; i++) {
preWhitespaceBuilder.append(whitespaceUnit);
}
int allNodes = 0;
String preWhitespace = preWhitespaceBuilder.toString();
for (int i = 0; i < subBranches.size(); i++) {
GraphNodeEntityTree br1 = subBranches.get(i);
String relationName = root.getRelationName(i, direction);
allNodes++;
System.out.println(preWhitespace + "->" +
relationName + "->" + br1.getVertex().getRawWord());
allNodes += traversalNodesWithDirection(br1, direction,
maxDepth, remainSearchDepth - 1);
}
return allNodes;
}
} 結果樣例如下:
->PEOPLE, direction:OUT, depth:10
->養寵物->:CAT
->吃->:RICE
->朋友->:DOG
->吃->:RICE
->吃->:RICE
->養寵物->:DOG
->吃->:RICE
->擁有->:HOUSE
->幹活->:JOB
->産出->:BRICK
->-構件->:HOUSE 看起來不錯,已經能夠展示出關系鍊了。當有多個入口時,使用','分隔另起一個描述即可。如果我們不考慮另一個複雜問題的話:環形關系問題。以上就足夠應付業務了。
ok,有了以上關系鍊的定義,我們可以很輕松地周遊出血緣關系了。而要實作真正地血緣分析,則肯定是資料驅動的,是以,你需要為每個關系定義一些原子查詢,這個查詢可以基于關系型資料庫實作,也可以基于redis之類的nosql實作,也可以基于es之類的産品實作。總之,底層可以任意更換。從外面看來,這和一個圖資料庫沒啥兩樣,主體-關系-客體同樣都有展現。在資料不大的情況下,不失為一個好的方法。當業務方向确立,需要進行更多更複雜業務時,再切換為真正的圖資料庫,使用圖計算,也是友善的。這也是一個正常的技術發展路線,不是嗎。
不要害怕今日的苦,你要相信明天,更苦!