手把手 | OpenAI開發可拓展元學習算法Reptile，能快速學習（附代碼）

在OpenAI, 我們開發了一種簡易的元學習算法，稱為Reptile。它通過對任務進行重複采樣，利用随機梯度下降法，并将初始參數更新為在該任務上學習的最終參數。

其性能可以和MAML（model-agnostic meta-learning，由伯克利AI研究所研發的一種應用廣泛的元學習算法）相媲美，操作簡便且計算效率更高。

MAML元學習算法：

http://bair.berkeley.edu/blog/2017/07/18/learning-to-learn/

元學習是學習如何學習的過程。此算法接受大量各種的任務進行訓練，每項任務都是一個學習問題，然後産生一個快速的學習器，并且能夠通過少量的樣本進行泛化。

一個深入研究的元學習問題是小樣本分類（few-shot classification），其中每項任務都是一個分類問題，學習器在每個類别下隻能看到1到5個輸入-輸出樣本（input-output examples），然後就要給新輸入的樣本進行分類。

下面是應用了Reptile算法的單樣本分類（1-shot classification）的互動示範，大家可以嘗試一下。

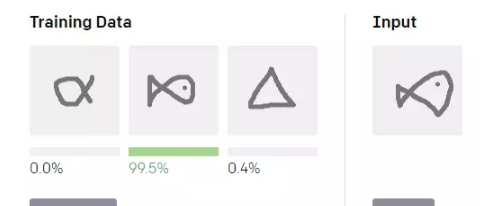
嘗試單擊“Edit All”按鈕，繪制三個不同的形狀或符号，然後在右側的輸入區中繪制其中一個，并檢視Reptile如何對它進行分類。前三張圖是标記樣本，每圖定義一個類别。最後一張圖代表未知樣本，Reptile要輸出此圖屬于每個類别的機率。

<b>Reptile的工作原理</b>

像MAML一樣，Reptile試圖初始化神經網絡的參數，以便通過新任務産生的少量資料來對網絡進行微調。

但是，當MAML借助梯度下降算法的計算圖來展開和區分時，Reptile隻是以标準方法在每個任務中執行随機梯度下降（stochastic gradient descent, SGD）算法，并不展開計算圖或者計算二階導數。這使得Reptile比MAML需要更少的計算和記憶體。示例代碼如下：

最後一步中,我們可以将Φ−W作為梯度，并将其插入像這篇論文裡（https://arxiv.org/abs/1412.6980）Adam這樣更為先進的優化器中作為替代方案。

首先令人驚訝的是，這種方法完全有效。如果k=1，這個算法就相當于 “聯合訓練”（joint training）——對多項任務的混合體執行SGD。雖然在某些情況下，聯合訓練可以學習到有用的初始化，但當零樣本學習（zero-shot learning）不可能實作時（比如，當輸出标簽是随機排列時），聯合訓練就幾乎無法學習得到結果。

Reptile要求k&gt;1，也就是說，參數更新要依賴于損失函數的高階導數實作，此時算法的表現和k=1（聯合訓練）時是完全不同的。

為了分析Reptile的工作原理，我們使用泰勒級數（Taylor series）來逼近參數更新。Reptile的更新将同一任務中不同小批量的梯度内積（inner product）最大化，進而提高了的泛化能力。

這一發現可能超出了元學習領域的指導意義，比如可以用來解釋SGD的泛化性質。進一步分析表明，Reptile和MAML的更新過程很相近，都包括兩個不同權重的項。

泰勒級數：

https://en.wikipedia.org/wiki/Taylor_series

在我們的實驗中，展示了Reptile和MAML在Omniglot和Mini-ImageNet基準測試中對少量樣本分類時産生相似的性能，由于更新具有較小的方差，是以Reptile也可以更快的收斂到解決方案。

Omniglot：

https://github.com/brendenlake/omniglot

Mini-ImageNet：

https://arxiv.org/abs/1606.04080

我們對Reptile的分析表明，通過不同的SGD梯度組合，可以獲得大量不同的算法。在下圖中，假設針對每一任務中不同小批量執行k步SGD，得出的梯度分别為g1,g2,…,gk。

下圖顯示了在 Omniglot 上由梯度之和作為元梯度而繪制出的學習曲線。g2對應一階MAML，也就是原先MAML論文中提出的算法。由于方差縮減，納入更多梯度明顯會加速學習過程。需要注意的是，僅僅使用g1（對應k=1）并不會給這個任務帶來改進，因為零樣本學習的性能無法得到改善。

X坐标：外循環疊代次數

Y坐标:Omniglot對比5種方式的

5次分類的準确度

<b>算法實作</b>

我們在GitHub上提供了Reptile的算法實作，它使用TensorFlow來完成相關計算，并包含用于在Omniglot和Mini-ImageNet上小樣本分類實驗的代碼。我們還釋出了一個較小的JavaScript實作，對TensorFlow預先訓練好的模型進行了微調。文章開頭的互動示範也是借助JavaScript完成的。

GitHub：

https://github.com/openai/supervised-reptile

較小的JavaScript實作：

https://github.com/openai/supervised-reptile/tree/master/web

最後，展示一個小樣本回歸（few-shot regression）的簡單示例，用以預測10(x,y)對的随機正弦波。該示例基于PyTorch實作，代碼如下：

原文釋出時間為：2018-04-11

本文作者：文摘菌