此前寫過一篇《BP算法基本原理推導----《機器學習》筆記》,但是感覺滿紙公式,而且沒有講到BP算法的精妙之處,是以找了一些資料,加上自己的了解,再來談一下BP。如有什麼疏漏或者錯誤的地方,還請大家不吝賜教。
說到反向傳播,無非四個字——“鍊式求導”,但實際上BP不止如此,BP是在這個基礎上,加入了一點動态規劃的機制。一般的BP包含以下幾個步驟:
前向傳導
反向傳播梯度計算
在反向傳播進行梯度計算的時候,BP不會進行重複計算,其原因就是在前向傳導的時候,進行了中間變量的存儲,并且在反向傳播的時候,可以進行DP。如果現在對這個過程不是很清楚,那麼不急,下一節我将用一個例子來直覺地說明BP算法的運作流程。
在講BP時,再啰嗦一下BP的應用場景:
BP算法适用于簡化多變量複合求導的過程
機器學習無非就是目标函數$Objective\ function $和一個學習算法,其中學習算法最基本的就是SGD(随機梯度下降),BP就可以用來計算其中的批梯度。
比如下面一個公式:
\[f(x,y)=\frac{x+\sigma(y)}{\sigma(x)+(x+y)^2}\ \ \ \ (1)
\]
注:\(\sigma(x)=\frac{1}{1+exp(-x)}\)
如果直接求出\(f(x,y)\)導數的解析解,你會發現這是一個很複雜的表達式,而且如果對多變量的每個變量都用解析的方式求解,那麼将會浪費更多的存儲空間以及無謂的重複計算。而使用BP,你可以看到一個清爽的求解過程,簡單的求解步驟。
我們使用上一節提出的公式(1)來講解BP具體是怎麼工作的。先來回顧一下公式(1):
我們使用計算圖的模型來表示這個計算過程。
實際上計算圖所做的工作就是将原本的複雜表達式分解成中間步驟的聚合。計算圖如下:
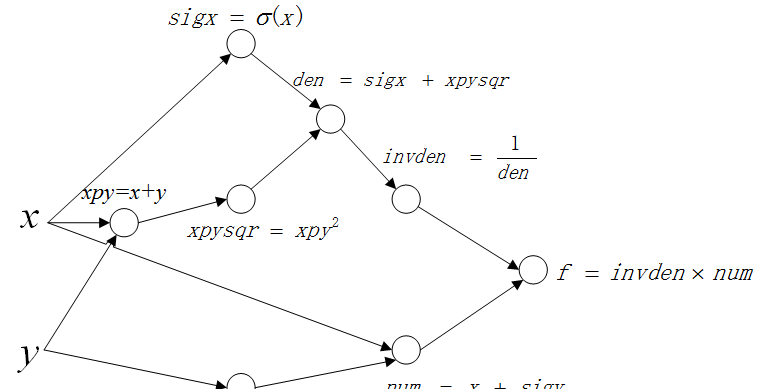
其中每個節點分别表示一個中間步驟,等式的左邊表示中間變量,右邊表示中間變量的解析表達。可以看到這個聚合的最終結果就是我們的公式(1)。
接下來說明BP怎麼根據這個計算圖進行梯度計算。
根據BP算法步驟,第一步就是前向傳播。
前向傳播很簡單,在傳播的過程中,我們儲存每一個中間變量的值,也就是每個中間節點的輸出值。
從輸出開始,反向傳播梯度值,計算輸出值對于每一個中間變量的梯度,并儲存,在上圖中就是 f。
一層一層來看這個傳播過程。
1)第一層
第一層傳播圖如下(紅色箭頭表示傳播方向):
以上面的路線為例:
這裡先計算 \(\frac{d(f)}{d(invden)}\),并儲存結果 \(dinvden\):
2)第二層
繼續以這條路線“反向傳播”計算第二層:
這裡要計算 \(\frac{d(f)}{d(den)}\),這裡不像第一層一樣,可以一次獲得結果,因為變量 \(den\) 和 \(f\) 中間隔着一個中間變量 \(invden\),是以需要用到鍊式法則(這裡就是鍊式求導在BP算法中的運用)。 鍊式推導如下:
\[\frac{d(f)}{d(den)}=\frac{d(f)}{d(invden)}\frac{d(invden)}{d(den)}\ \ \ \ (2)
根據原始計算圖以及上一步的中間結果:
\[invden = \frac{1}{den}\ \ \ \ (3)
(2)(3)聯立,得:
\[dden=dinvden\times \frac{-1}{den^2}\ \ \ \ (4)
整個計算過程展示如下:
就這樣,BP不斷地反向傳播梯度,并儲存中間梯度,直到計算圖的所有中間值以及初始值的梯度被求解完畢。
根據以上過程,總結BP算法具體需要以下幾個步驟。
可以注意到,在梯度回傳的過程中需要用到節點的輸出值,是以在前向傳播的過程中需要儲存每個節點的輸出值。同時,輸出值關于輸入值的梯度也可以馬上獲得,這在反向傳播的求解中也需要用到。是以前向傳導記錄以下兩個值:
中間結點的輸出值
輸出值關于輸入值的梯度
反向傳播
反向傳播就是一個計算網絡最終輸出值關于自己輸出的梯度的過程。
知乎傳送門
怕什麼真理無窮,進一寸有一寸的歡喜