智能優化算法又稱現代啟發式算法,是一種具有全局優化性能、通用性強且适合于并行處理的算法。這種算法一般具有嚴密的理論依據,而不是單純憑借專家經驗,理論上可以在一定的時間内找到最優解或近似最優解。常用的智能優化算法有:遺傳算法 、模拟退火算法、禁忌搜尋算法、粒子群算法、蟻群算法。
本文主要為大家帶來遺傳算法和蟻群算法的詳細解讀。
1. 遺傳算法
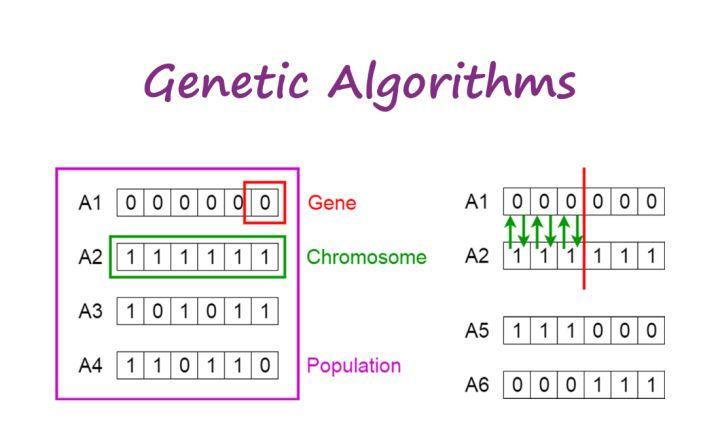
遺傳算法(Genetic algorithm, GA),模拟生物在自然環境中遺傳和進化的自适應(對遺傳參數的自适應調整)全局優化(随機變異不斷尋找全局最優解)算法,基本思想是“優勝劣汰”,是應用最廣泛和效果最顯著的智能優化算法。
1.1 編碼方法
算法模型通過對個體(individual,也即solution)進行二進制編碼(01編碼)、自然數編碼、實數編碼和樹型編碼。在對個體進行适應度計算時需要進行解碼,實作問題的解空間與算法搜尋空間的互相轉換。
1.2 适應度函數
每個個體都有一個适應度函數(Fitness),對這個個體的優劣進行定量評價,适應度函數是算法執行“适者生存、優勝劣汰”的依據。适應度函數需要根據目标函數進行設定,令g(x)g(x)表示目标函數,令G(x)G(x)表示适應度函數,從目标函數g(x)g(x)映射到适應度函數G(x)G(x)的過程稱為标定。
對于最大值優化問題,可直接将g(x)g(x)設定為适應度函數G(x)G(x),即G(x)=g(x)G(x)=g(x);對于最小值優化問題,G(x)=-\min g(x)G(x)=−ming(x);在遺傳算法規定中,适應度函數為正值,但上述二式無法保證,是以需要加上最小值或者最大值以及分段函數。
1.3 選擇操作
選擇(Selection)是從目前群體中選擇适應度函數值大的個體,這些優良個體有可能作為父代繁殖下一代,個體适應度函數越大,被選擇作為父代的機率越大(有可能!)
選擇算法有很多,最基本的是輪盤賭算法:
其中,P_iPi表示個體被選擇的機率;F_iFi表示個體的适應度函數值;NN表示種群規模。
根據選擇機率P_iPi将圓盤形賭輪分為NN份,第ii個扇形的中心角為2\pi P_i2πPi。随機産生0到1之間服從均勻分布的數rr,落在第ii個扇形的累計機率為Q_i = \sum_{j=1}^i P_jQi=∑j=1iPj,則選擇個體ii,重複NN次,就可以選擇NN個個體。
1.4 交叉操作
兩個個體通過交叉(Crossover)互換染色體部分基因而重組産生新的個體,也就是産生新解。交叉前需要進行随機配對。
一般情況下,對二進制編碼的個體采用點交叉的方法,也就是在兩個配對字元串随機選擇一個或者多個交叉點,互換部分子串進而産生新的字元串
兩個個體是否進行交叉操作由交叉機率決定,較大的交叉機率可以使遺傳算法産生更多新解,保持群體多樣性,并能防止算法過早成熟,但是交叉機率過大會使算法過多搜尋不必要的解區域,消耗過多的計算時間,一般取值在0.9左右。
1.5 變異操作
生物進化中,某些染色體可能會發生基因突變(Mutation),進而産生新的染色體,這也是産生新解的另外一種重要方式。交叉操作相當于進行全局探索,變異操作相當于進行局部開發,這也是智能優化算法必備的兩種搜尋能力。
個體能否變異取決于變異機率,過低會使得部分有用基因無法進入染色體,不能提高解的品質;過大會使子代喪失父代優良基因,導緻算法失去從過去搜尋經驗的學習能力,一般情況下,變異機率取值為0.005左右。
值得注意的是,Rudolph通過馬爾科夫鍊相關理論證明僅采用選擇、交叉和變異三個操作的遺傳算法不能收斂到全局最優解,而采用精英保留政策的遺傳算法是全局收斂的。
算法的整體流程如下圖所示:
1.6 算法分析
一個好的智能算法,關鍵在于全局探索和局部開發能力的平衡。全局探索的目的是對解空間進行更全面的探索,局部開發主要目的是對已知區域進行更精細的搜尋,希望獲得品質更好的新解。
遺傳算法可以通過設定選擇壓力實作全局探索和局部開發的平衡。在算法運作初始階段,設定較小的選擇壓力可以使算法具有較好的全局探索能力,進行廣域搜尋;算法運作後期,設定較大的選擇壓力可以使算法進行比較精細的局部搜尋。
選擇壓力的設定可以從适應度函數标定和選擇政策。
适應度函數标定,在算法早期,應當縮小個體适應度差距,減少淘汰率;算法運作最後階段,擴大個體适應度差距,保證算法能在高适應度個體對應解區域進行集中搜尋,加快算法收斂速度。常用方法有:
選擇政策,低選擇壓力可選擇多種類型的個體,加強對未知解區域的搜尋,避免算法陷入局部極值,但算法優化速度會變得緩慢;高選擇壓力可選擇優良個體,加快優化速度但群體多樣性會下降,減少搜尋到全局最優值的機率。除了輪盤賭算法外,選擇政策還有:
- 分級選擇法
- 錦标賽選擇法
- Boltzmann選擇法
2.蟻群算法
2.1 蟻群優化算法
蟻群優化(Ant Colony Optimization, ACO)算法是源自大自然生物界的仿真類算法,其思想吸收了蟻群覓食過程中的行為特性。蟻群算法在TSP問題、二次配置設定問題、圖着色問題、車輛排程問題、通信網絡中的負載均衡問題等表現出良好的優化性能。
大自然中的螞蟻沒有視覺,依賴于同類散發在環境中的資訊素決定自己何去何從,孤立的螞蟻沿着同伴的資訊素軌迹移動,同時釋放自己的資訊素,進而增強了該路線上的資訊素數量,随着越來越多的螞蟻通過該路線,一條較佳的路線就形成了(這條路徑不一定最短,但對于NP-hard問題而言足夠了)。
2.2. 算法模型
以旅行商問題(Traveling Salesman Problem, TSP)為例,在圖論中稱為最小Hamilton問題。
蟻群優化算法基本模型:
- 螞蟻群體總是尋找最小費用可行解
- 螞蟻具有記憶性,存儲目前路徑的資訊,構造可行解、評價解的品質、路徑反向追蹤
- 目前狀态的螞蟻可以移動到可行領域任意一點
- 每個螞蟻賦予一個初始狀态和若幹個終止條件
- 螞蟻從初始狀态到可行領域狀态,以遞推方式構造解,當有一個螞蟻滿足至少一個終止條件時構造過程結束
- 螞蟻按某種機率決策規則移動至領域結點
- 移動後資訊素軌迹被更新,過程稱為“單步線上資訊素更新”
- 一旦構造出一個解,螞蟻沿原路方向追蹤,更新資訊素軌迹,稱為“線上延遲資訊素更新”
2.3 算法分析
算法複雜度是O(nc\cdot n^2\cdot m)O(nc⋅n2⋅m),m為螞蟻個數,nc為疊代次數或者搜尋次數,n為頂點數。算法運作效果受到\alpha, \betaα,β等參數影響,其中\betaβ的影響在于展現資訊素軌迹的持久性,數值過小意味着資訊消失過快;數值過大容易落入局部最優點,是以其數值通常取0.7左右。
在基本的蟻群優化算法上,可以與其他啟發式算法相結合,最典型的就是嵌入局部搜尋算法,在各個螞蟻形成自己的路線後,用局部調整方法(2-opt, 3-opt)加以改進,此外,與遺傳算法、模拟退火和禁忌搜尋等結合也有一定的成效。
混合蟻群優化算法主要步驟:
- Begin
- 螞蟻初始化;
- LOOP:
- \quad螞蟻路徑構造;
- \quad對某個螞蟻實施局部搜尋算法
- \quad螞蟻軌迹更新
- \quad若疊代次數未到,轉LOOP;
- 輸出目前最好解
- End