考慮一個有序表:14->23->34->43->50->59->66->72
從該有序表中搜尋元素 < 23, 43, 59 > ,需要比較的次數分别為 < 2, 4, 6 >,總共比較的次數
為 2 + 4 + 6 = 12 次。有沒有優化的算法嗎? 連結清單是有序的,但不能使用二分查找。類似二叉
搜尋樹,我們把一些節點提取出來,作為索引。
這裡我們把 < 14, 34, 50, 72 > 提取出來作為一級索引,這樣搜尋的時候就可以減少比較次數了。
我們還可以再從一級索引提取一些元素出來,作為二級索引,變成如下結構:
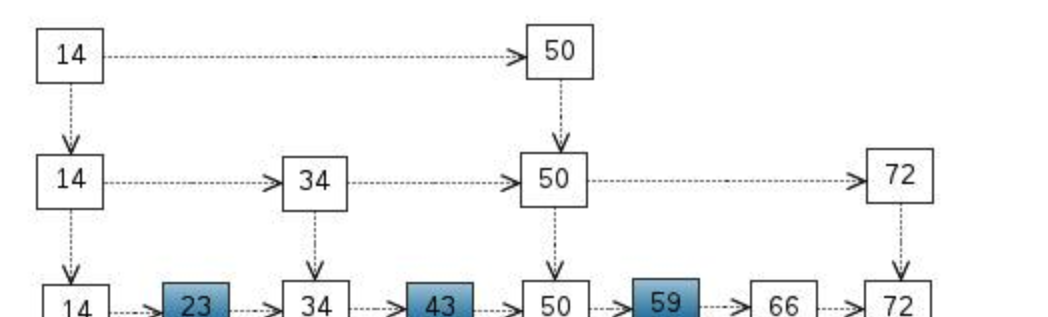
如果元素足夠多,這種索引結構就能展現出優勢來了。
跳表具有如下性質:
(1) 由很多層結構組成
(2) 每一層都是一個有序的連結清單
(3) 最底層(Level 1)的連結清單包含所有元素
(4) 如果一個元素出現在 Level i 的連結清單中,則它在 Level i 之下的連結清單也都會出現。
(5) 每個節點包含兩個指針,一個指向同一連結清單中的下一個元素,一個指向下面一層的元素。
其中 -1 表示 INT_MIN, 連結清單的最小值,1 表示 INT_MAX,連結清單的最大值。
例子:查找元素 117
(1) 比較 21, 比 21 大,往後面找
(2) 比較 37, 比 37大,比連結清單最大值小,從 37 的下面一層開始找
(3) 比較 71, 比 71 大,比連結清單最大值小,從 71 的下面一層開始找
(4) 比較 85, 比 85 大,從後面找
(5) 比較 117, 等于 117, 找到了節點。
新節點和各層索引節點逐一比較,确定原連結清單的插入位置。O(logN)
把索引插入到原連結清單。O(1)
利用抛硬币的随機方式,決定新節點是否提升為上一級索引。結果為“正”則提升并繼續抛硬币,結果為“負”則停止。O(logN)
總體上,跳躍表插入操作的時間複雜度是O(logN),而這種資料結構所占空間是2N,既空間複雜度是 O(N)。
自上而下,查找第一次出現節點的索引,并逐層找到每一層對應的節點。O(logN)
删除每一層查找到的節點,如果該層隻剩下1個節點,删除整個一層(原連結清單除外)。O(logN)
總體上,跳躍表删除操作的時間複雜度是O(logN)。
跳躍表的優點在維持結構平衡的成本比較的,根據扔硬币,是以完全依靠随機。而二叉查找樹在多次插入删除後,需要Rebalance來重新調整結構平衡。