二項式定理與組合恒等式的部分證明

證明以下組合恒等式

\[\dbinom{n}{k}=\dbinom{n}{n-k}

\]

\[\dbinom{n}{k}=\dfrac{n}{k}\cdot\dbinom{n-1}{k-1}

\(\dbinom{n}{k}\) 的組合意義相當于 \(n\) 個物體中取出 \(k\) 個物體的方案數，而在 \(n\) 個物體中取出 \(k\) 個物體後，就還剩下 \(n-k\) 個物體廢話，則 \(n\) 個物體中取出 \(k\) 個物體的方案數與 \(n\) 個物體中取出 \(n-k\) 個物體的方案數相同，即 \(\dbinom{n}{k}=\dbinom{n}{n-k}\)

原公式成立，證畢。

\(\because\) 左邊 \(=\dbinom{n}{k}=\dfrac{n!}{k!(n-k)!}=\dfrac{n}{k}\cdot\dfrac{(n-1)!}{(k-1)!(n-k)!}=\dfrac{n}{k}\cdot\dbinom{n-1}{k-1}=\) 右邊

證明 \(Pascal\) 公式

\[\dbinom{n}{k}=\dbinom{n-1}{k}+\dbinom{n-1}{k-1}

\(\dbinom{n}{k}\) 的組合意義相當于 \(n\) 個物體中取出 \(k\) 個物體的方案數，而我們可以指定第 \(n\) 個物體的取否，也可以得到方案數。

當取第 \(n\) 個物體時，還剩下 \(n-1\) 個物體，還可以選擇 \(k-1\) 個物體，方案數為 \(\dbinom{n-1}{k-1}\)

當不取第 \(n\) 個物體時，還剩下 \(n-1\) 個物體，還可以選擇 \(k\) 個物體，方案數為 \(\dbinom{n-1}{k}\)

\(\large{\therefore}\) 方案數也可以表示為 \(\dbinom{n-1}{k-1}+\dbinom{n-1}{k}\)

\(\therefore\dbinom{n}{k}=\dbinom{n-1}{k}+\dbinom{n-1}{k-1}\)

證明二項式定理：

\[(x+y)^n=\displaystyle\sum^{n}_{k=0}\dbinom{n}{k}x^{n-k}y^{k}

當 \(n=1\) 時，\((x+y)^n=x+y\)，顯然成立。

假設 \(n=k\) 時公式成立, 即證 \(n=k+1\) 時公式也成立

\(\because (x+y)^{k+1}=(x+y)(x+y)^k\)

\(\therefore(x+y)^{k+1}=(x+y)(\displaystyle\sum^{k}_{i=0}\dbinom{k}{i}x^{k-i}y^{i})\)

\(\therefore(x+y)^{k+1}=\displaystyle\sum^{k}_{i=0}\dbinom{k}{i}x^{k-i+1}y^{i}+\displaystyle\sum^{k}_{i=0}\dbinom{k}{i}x^{k-i}y^{i+1}\)

\(\therefore(x+y)^{k+1}=\dbinom{k}{0}x^{k+1}+\displaystyle\sum^{k}_{i=1}\dbinom{k}{i}x^{k-i+1}y^{i}+\dbinom{k}{k}y^{k+1}+\displaystyle\sum^{k-1}_{i=0}\dbinom{k}{i}x^{k-i}y^{i+1}\)

變限合并得:

\(\therefore(x+y)^{k+1}=\dbinom{k}{0}x^{k+1}+\displaystyle\sum^{k}_{i=1}\big[\dbinom{k}{i}+\dbinom{k}{i-1}\big]x^{k-i+1}y^{i}+\dbinom{k}{k}y^{k+1}\)

由 \(Pascal\) 公式得:

\(\dbinom{n}{k}=\dbinom{n-1}{k}+\dbinom{n-1}{k-1}\)

\(\therefore(x+y)^{k+1}=\dbinom{k}{0}x^{k+1}+\displaystyle\sum^{k}_{i=1}\dbinom{k+1}{i}x^{k-i+1}y^{i}+\dbinom{k}{k}y^{k+1}\)

\(\therefore(x+y)^{k+1}=\displaystyle\sum^{k}_{i=0}\dbinom{k+1}{i}x^{k-i+1}y^{i}\)

即得:當 \(n=k\) 公式成立時, \(n=k+1\) 時公式也成立

綜上，原公式成立，證畢。

由此，我們也可以通過改變 \(x\) 和 \(y\) 的取值，得到以下公式：

當 \(x=y=1\) 時，\((x+y)^n=(1+1)^n=2^n=\displaystyle\sum^{n}_{k=0}\dbinom{n}{k}\)

\(\therefore\displaystyle\sum^{n}_{k=0}\dbinom{n}{k}=2^n\)

當 \(x=1\)，\(y=-1\) 時，\((x+y)^n=(1+(-1))^n=0=\displaystyle\sum^{n}_{k=0}(-1)^k\dbinom{n}{k}\)

\(\therefore\displaystyle\sum^{n}_{k=0}(-1)^k\dbinom{n}{k}=0\)

證明

\[\displaystyle\sum^n_{k=0}k\dbinom{n}{k}=n\cdot2^{n-1}

如果不了解求導的朋友可以看一下這一篇文章 連結

\(\because (1+x)^{n}=\displaystyle\sum^{n}_{k=0}\dbinom{n}{k}x^{k}=\displaystyle\sum^{n}_{k=1}\dbinom{n}{k}x^{k}+1\)

求導得:

\(n(1+x)^{n-1}=\displaystyle\sum^{n}_{k=1}k\cdot \dbinom{n}{k}x^{k-1}\)

又因為 \(\displaystyle\sum^{n}_{k=0}\dbinom{n}{k}=2^n\)

\(\therefore\)當 \(x=1\) 時，\(n\cdot2^{n-1}=\displaystyle\sum^{n}_{k=1}k\dbinom{n}{k}\)

通過變限得：

\(\displaystyle\sum^n_{k=0}k\dbinom{n}{k}=n\cdot2^{n-1}\)

\[\displaystyle\sum^n_{k=0}k^2\dbinom{n}{k}=n(n+1)\cdot2^{n-2}

由 \(\dbinom{n}{k}=\dfrac{n}{k}\dbinom{n-1}{k-1}\) 得：

\(\displaystyle\sum^n_{k=0}k^2\dbinom{n}{k}=\displaystyle\sum^n_{k=1}k^2\cdot \dfrac{n}{k}\dbinom{n-1}{k-1}=\displaystyle\sum^n_{k=1}k\cdot n\dbinom{n-1}{k-1}\)

将 \(n\) 提出，并配湊 \(k-1\) 後,式子變為 \(n\displaystyle\sum^n_{k=1}[(k-1)+1]\dbinom{n-1}{k-1}\)

\(\therefore\) 原式 \(=n\displaystyle\sum^n_{k=1}[(k-1)+1]\dbinom{n-1}{k-1}=n\displaystyle\sum^n_{k=1}(k-1)\dbinom{n-1}{k-1}+n\displaystyle\sum^n_{k=1}\dbinom{n-1}{k-1}\)

\(\because\displaystyle\sum^{n}_{k=0}\dbinom{n}{k}=2^n\)

\(\therefore\) 原式 \(=n\displaystyle\sum^n_{k=1}(k-1)\dbinom{n-1}{k-1}+n\cdot 2^{n-1}\)

通過變限得:

原式 \(=n\displaystyle\sum^n_{k=0}k\dbinom{n-1}{k}+n\cdot 2^{n-1}=n(n-1)\cdot 2^{n-2}+n\cdot 2^{n-1}=n(n+1)\cdot2^{n-2}\)

\[\displaystyle\sum^n_{l=0}\dbinom{l}{k}=\dbinom{n+1}{k+1}\ n,k \in N

\(\dbinom{n+1}{k+1}\) 的組合意義相當于集合 \(S=\{a_1,a_2,a_3\cdots a_n,a_{n+1}\}\) 中集合大小為 \(k+1\) 子集數。

而子集數也可以通過指定某些集合元素的取否來算出。

當 \(a_1\) 在子集中，此時有一共 \(\dbinom{n}{k}\) 個集合大小為 \(k+1\) 的子集。

當 \(a_2\) 在子集中，且 \(a_1\) 不在子集中，此時有一共 \(\dbinom{n-1}{k}\) 個集合大小為 \(k+1\) 的子集。

\(\large{\cdots\cdots}\)

當 \(a_n\) 在子集中，且 \(a_1,a_2\cdots a_{n-1}\) 不在子集中，此時有一共 \(\dbinom{1}{k}\) 個集合大小為 \(k+1\) 的子集。

當 \(a_{n+1}\) 在子集中，且 \(a_1,a_2\cdots a_{n}\) 不在子集中，此時有一共 \(\dbinom{0}{k}\) 個集合大小為 \(k+1\) 的子集。

綜上，共有 \(\dbinom{n}{k}+\dbinom{n-1}{k}+\cdots+\dbinom{1}{k}+\dbinom{0}{k}=\displaystyle\sum^n_{l=0}\dbinom{l}{k}\) 個集合大小為 \(k+1\) 的子集。

由此可得：\(\displaystyle\sum^n_{l=0}\dbinom{l}{k}=\dbinom{n+1}{k+1}\)

\[\dbinom{n}{r}\dbinom{r}{k}=\dbinom{n}{k}\dbinom{n-k}{r-k}

\(\dbinom{n}{r}\dbinom{r}{k}\) 的組合意義相當于一個大小為 \(n\) 的集合中先取出 \(r\) 個元素，再從這 \(r\) 個元素中取出 \(k\) 個元素的方案數。

而我們是否能直接以這些 \(k\) 元子集的數目 \(\dbinom{n}{k}\) 代替之前所提的方案數呢?

答案是不能廢話不，因為不同的 \(r\) 元子集可能會取出相同的 \(k\) 元子集(如圖)

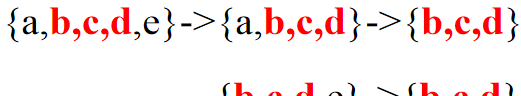
是以,我們還要算上這些這些能選出相同 \(k\) 元子集的 \(r\) 元子集,即乘上 \(\dbinom{n-k}{r-k}\)

綜上,集合中先取出 \(r\) 個元素，再從這 \(r\) 個元素中取出 \(k\) 個元素的方案數也等于 \(\dbinom{n}{k}\dbinom{n-k}{r-k}\)

是以，\(\dbinom{n}{r}\dbinom{r}{k}=\dbinom{n}{k}\dbinom{n-k}{r-k}\)

\[\displaystyle\sum^{r}_{k=0}\dbinom{m}{k}\dbinom{n}{r-k}=\dbinom{n+m}{r}

\(\displaystyle\sum^{r}_{k=0}\dbinom{m}{k}\dbinom{n}{r-k}\) 的組合意義相當于先在一個大小為 \(n\) 的集合中取出 \(k\) 個元素，再在一個大小為 \(m\) 的集合中取出 \(r-k\) 個元素的方案數。

由于在 \(n\) 元集合中取值與在 \(m\) 元集合中取值互不幹擾顯然，是以我們可以将兩個集合合并，并在合并後的集合中取出 \(r\) 個元素，這樣操作後方案數并不會發生改變，此時方案數為 \(\dbinom{n+m}{r}\)

綜上，\(\displaystyle\sum^{r}_{k=0}\dbinom{m}{k}\dbinom{n}{r-k}=\dbinom{n+m}{r}\)

通過改變 \(r\) 的取值，我們還可以得到下面這個式子：

當 \(r=m\) 時，\(\displaystyle\sum^{r}_{k=0}\dbinom{m}{k}\dbinom{n}{r-k}=\displaystyle\sum^{m}_{k=0}\dbinom{m}{k}\dbinom{n}{m-k}=\dbinom{n+m}{m}\)

整理得：

\(\displaystyle\sum^{m}_{k=0}\dbinom{n}{k}\dbinom{m}{k}=\dbinom{n+m}{m}\)

完結撒花