排序算法
排序算法算是我們學習算法的入門篇,在正式介紹各種排序算法前,先介紹一下要用到的一些術語:
穩定排序:如果a本來在b的前面,且a==b,排序以後a依舊在b的前面,那就是穩定排序,否在是非穩定排序
原地排序:就是在排序過程中不申請多于的存儲空間,隻利用原來存儲待排資料的存儲空間進行比較和交換的資料排序。而非原地排序就是需要利用額外的數組來輔助排序。
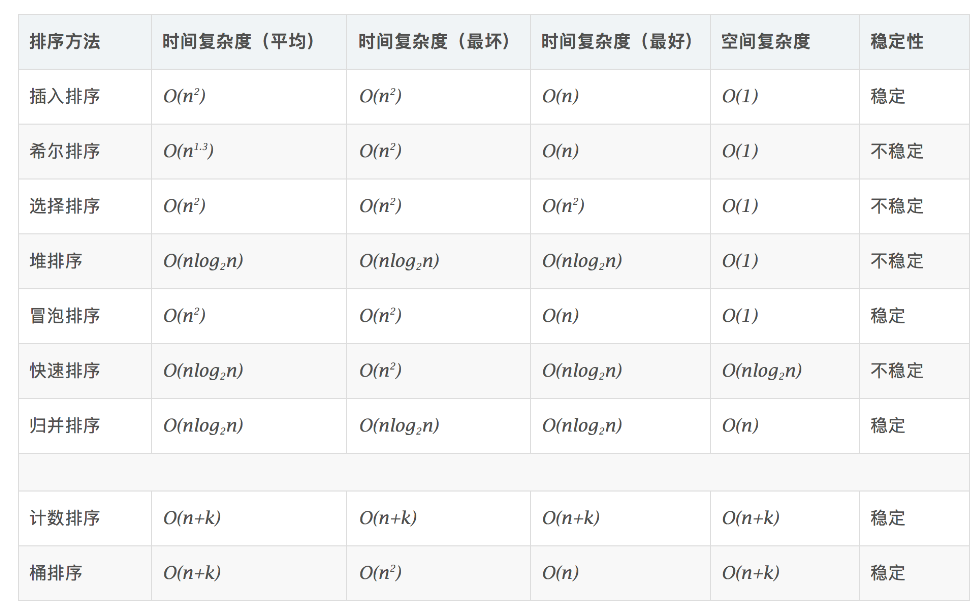
總覽:
首先找到數組中最小的元素,其次将其與數組中第一個元素交換位置,然後在剩下的數組中找到最小的元素,然後和第二個元素交換,以此類推,直到交換完畢。
資料移動最少,運作時間與資料輸入時的順序無關
時間複雜度:O(n²)
空間複雜度:O(1)
非穩定排序
原地排序
資料量少
像抓牌一樣,将牌暫時放入現在的适當的位置。當到最後一個元素時就排序完成了。就像把一個無序數組中的資料整合到一個有序數組中。
運作時間與輸入情況有關,對于一個部分有序(數組中元素離最終位置都不遠,或者一個有序的大數組加一個小數組)來說速度比較快
穩定排序
數組基本有序,或者一個有序的大數組中添加一些小資料。
十分簡單,重複通路,依次比較進行交換,交換過多
比較相鄰元素,大就交換
從第一對開始,到最後一對,一次排序後保證最大的位于末尾
重複n次
思路簡單
時間複雜度:O(n2)
無适用場景一般用于學習算法。
改良冒泡排序算法 在我們周遊的過程中,會發現從開始第一隊到最後一對都沒有發生交換,此時意味着,剩下這些待排序的元素已經是有序的資料,無序再次排序,是以我們可以引入一個标志,當遇到此情況的時候,直接跳出循環。減少無意義的比較和縮短排序時間。
希爾排序是插入排序的一種變種,原來插入排序的優勢在于資料基本有序的情況下性能很好,但是如果原數組中的元素距離其正确位置很遠的話,效率就不是很高,而希爾排序正是優化了這一點。
希爾排序就是為了加快速度簡單的改進了插入排序,交換不相鄰的元素以對資料的局部進行排序。
先使數組中任意間隔為h的元素是有序的。最後對于一個以1結尾的的h序列我們都能夠将其排序。
具體步驟:
先将整個待排序的記錄序列分隔成若幹子序列,分别進行直接插入排序
選擇一個增量序列t1,t2,…,tk,其中ti>tj,tk=1;
按增量序列個數k,對序列進行k 趟排序;
每趟排序,根據對應的增量ti,将待排序列分割成若幹長度為m 的子序列,分别對各子表進行直接插入排序。僅增量因子為1 時,整個序列作為一個表來處理,表長度即為整個序列的長度。
基于插入排序的快速排序
時間複雜度:O(nlogn)
大型數組,大多數情況下希爾排序都是比較高效且簡單的算法
需要注意的是,對各個分組進行插入的時候并不是先對一個組排序完了再對另一個組排序,而是輪流對每個組進行排序。
将一個大的無序數組有序,我們可以利用歸并的思想來進行排序,即将大問題化為小問題進行解決。
把長度為n的輸入序列分成兩個長度為n/2的子序列;
對這兩個子序列分别采用歸并排序;
将兩個排序好的子序列合并成一個最終的排序序列。
速度較快,不受輸入資料的影響,所需額外空間與N成正比
空間複雜度:O(n)
非原地排序
我們從數組中選擇一個元素,我們把這個元素稱之為中軸元素吧,然後把數組中所有小于中軸元素的元素放在其左邊,所有大于或等于中軸元素的元素放在其右邊,顯然,此時中軸元素所處的位置的是有序的。也就是說,我們無需再移動中軸元素的位置。
從中軸元素那裡開始把大的數組切割成兩個小的數組(兩個數組都不包含中軸元素),接着我們通過遞歸的方式,讓中軸元素左邊的數組和右邊的數組也重複同樣的操作,直到數組的大小為1,此時每個元素都處于有序的位置。
應用廣泛,原地排序,幾乎不需要額外的空間
空間複雜度:O(logn)
廣泛
利用堆這種資料結構,堆積是一個近似完全二叉樹的結構,并同時滿足堆積的性質:即子結點的鍵值或索引總是小于(或者大于)它的父節點。
将初始待排序關鍵字序列(R1,R2….Rn)建構成大頂堆,此堆為初始的無序區;
将堆頂元素R[1]與最後一個元素R[n]交換,此時得到新的無序區(R1,R2,……Rn-1)和新的有序區(Rn),且滿足R[1,2…n-1]<=R[n];
由于交換後新的堆頂R[1]可能違反堆的性質,是以需要對目前無序區(R1,R2,……Rn-1)調整為新堆,然後再次将R[1]與無序區最後一個元素交換,得到新的無序區(R1,R2….Rn-2)和新的有序區(Rn-1,Rn)。不斷重複此過程直到有序區的元素個數為n-1,則整個排序過程完成。
計數排序是一種适合于最大值和最小值的內插補點不是不是很大的排序。
基本思想:就是把數組元素作為數組的下标,然後用一個臨時數組統計該元素出現的次數,例如 temp[i] = m, 表示元素 i 一共出現了 m 次。最後再把臨時數組統計的資料從小到大彙總起來,此時彙總起來是資料是有序的。
時間複雜度:O(n+k)
空間複雜度:O(n+k)
其排序速度快于任何比較排序算法。當k不是很大并且序列比較集中時,計數排序是一個很有效的排序算法。
桶排序是計數排序的更新版。它利用了函數的映射關系,高效與否的關鍵就在于這個映射函數的确定。桶排序 (Bucket sort)的工作的原理:假設輸入資料服從均勻分布,将資料分到有限數量的桶裡,每個桶再分别排序(有可能再使用别的排序算法或是以遞歸方式繼續使用桶排序進行排)。
設定一個定量的數組當作空桶;
周遊輸入資料,并且把資料一個一個放到對應的桶裡去;
對每個不是空的桶進行排序;
從不是空的桶裡把排好序的資料拼接起來。
桶排序最好情況下使用線性時間O(n),桶排序的時間複雜度,取決與對各個桶之間資料進行排序的時間複雜度,因為其它部分的時間複雜度都為O(n)。很顯然,桶劃分的越小,各個桶之間的資料越少,排序所用的時間也會越少。但相應的空間消耗就會增大
基數排序是按照低位先排序,然後收集;再按照高位排序,然後再收集;依次類推,直到最高位。有時候有些屬性是有優先級順序的,先按低優先級排序,再按高優先級排序。最後的次序就是高優先級高的在前,高優先級相同的低優先級高的在前。
取得數組中的最大數,并取得位數;
arr為原始數組,從最低位開始取每個位組成radix數組;
對radix進行計數排序(利用計數排序适用于小範圍數的特點);
針對計數排序進行優化的一種算法。
時間複雜度:O(kn)
代碼思路倒是很簡單,就是利用線程睡眠來進行排序,讓線程睡眠、
娛樂算法,沒啥特點就是好玩
就是讓系統随機排序,然後驗證是否有序
巨複雜,看命
如果覺得看完有收獲,希望能給我點個贊,這将會是我更新的最大動力,感謝各位的支援
歡迎各位關注我的公衆号【java冢狐】,專注于java和計算機基礎知識,保證讓你看完有所收獲,不信你打我
如果看完有不同的意見或者建議,歡迎多多評論一起交流。感謝各位的支援以及厚愛。
——我是冢狐,和你一樣熱愛程式設計。