演講嘉賓簡介:
孫飛(丹豐),阿裡巴巴搜尋事業部進階算法工程師。中科院計算所博士,博士期間主要研究方向為文本分布式表示,在SIGIR、ACL、EMNLP以及IJCAI等會議發表論文多篇。目前主要從事推薦系統以及文本生成相關方面研發工作。
以下内容根據演講嘉賓視訊分享以及PPT整理而成。
本次的分享主要圍繞以下五個方面:
神經網絡的發展曆史
感覺器模型
前饋神經網絡
後向傳播
深度學習入門
一.神經網絡的發展曆史
在介紹神經網絡的發展曆史之前,首先介紹一下神經網絡的概念。神經網絡主要是指一種仿造人腦設計的簡化的計算模型,這種模型中包含了大量的用于計算的神經元,這些神經元之間會通過一些帶有權重的連邊以一種階層化的方式組織在一起。每一層的神經元之間可以進行大規模的并行計算,層與層之間進行消息的傳遞。
下圖展示了整個神經網絡的發展曆程:
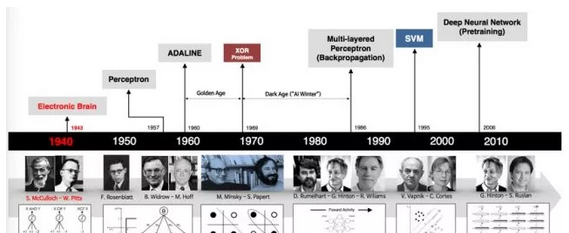
神經網絡的發展曆史甚至要早于計算機的發展,早在上個世紀四十年代就已經出現了最早的神經網絡模型。接下來本文将以神經網絡的發展曆程為主線帶領大家對神經網絡的基本知識作初步了解。
第一代的神經元模型是驗證型的,當時的設計者隻是為了驗證神經元模型可以進行計算,這種神經元模型既不能訓練也沒有學習能力,可以簡單的把它看成是一個定義好的邏輯門電路,因為它的輸入和輸出都是二進制的,而中間層的權重都是提前定義好的。
神經網絡的第二個發展時代是十九世紀五六十年代,以Rosenblatt提出的感覺器模型和赫伯特學習原則等一些工作為代表。
二.感覺器模型
感覺器模型與之前提到的神經元模型幾乎是相同的,但是二者之間存在着一些關鍵的差別。感覺器模型的激活函數可以選擇間斷函數和sigmoid函數,且其輸入可以選擇使用實數向量,而不是神經元模型的二進制向量。與神經元模型不同,感覺器模型是一個可以學習的模型,下面介紹一下感覺器模型的一個優良特性——幾何解釋。
我們可以把輸入值(x1, . . . , xn)看作是N維空間中的一個點的坐标,w⊤x−w0 = 0 可以認為是N維空間中的一個超平面,顯然,當w⊤x−w0<0時,此時的點落在超平面的下方,而當w⊤x−w0>0時,此時的點落在超平面的上方。感覺器模型對應的就是一個分類器的超平面,它可以将不同類别的點在N維空間中分離開。從下圖中可以發現,感覺器模型是一個線性的分類器。
對于一些基本的邏輯運算,例如與、或、非,感覺器模型可以非常容易地作出判斷分類。那麼是不是所有的邏輯運算都可以通過感覺器進行分類呢?答案當然是否定的。比如異或運算通過一個單獨的線性感覺器模型就很難作出分類,這同樣也是神經網絡的發展在第一次高潮之後很快進入低谷的主要原因。這個問題最早在Minsky等人在關于感覺器的著作中提出,但其實很多人對這本著作存在誤區,實際上Minsky等人在提出這個問題的同時也指出異或運算可以通過多層感覺器實作,但是由于當時學術界沒有有效的學習方式去學習多層感覺器模型,是以神經網絡的發展迎來了第一次低谷。
關于多層感覺器模型實作異或操作的直覺幾何展現如下圖所示:
三.前饋神經網絡
進入十九世紀八十年代之後,由于單層的感覺器神經網絡的表達能力非常有限,隻能做一些線性分類器的任務,神經網絡的發展進入了多層感覺器時代。一個典型的多層神經網絡就是前饋神經網絡,如下圖所示,它包括輸入層、節點數目不定的隐層和輸出層。任何一個邏輯運算都可以通過多層感覺器模型表示,但這就涉及到三層之間互動的權重學習問題。将輸入層節點xk乘以輸入層到隐層之間的權重vkj,然後經過一個如sigmoid此類的激活函數就可以得到其對應的隐層節點數值hj,同理,經過類似的運算可以由hj得出輸出節點值yi。
需要學習的權重資訊就是w和v兩個矩陣,最終得到的資訊是樣本的輸出y和真實輸出d。具體過程如下圖所示:
如果讀者有簡單的機器學習知識基礎的話,就會知道一般情況下會根據梯度下降的原則去學習一個模型。在感覺器模型中采用梯度下降的原則是較為容易的,以下圖為例,首先确定模型的loss,例子中采用了平方根loss,即求出樣本的真實輸出d與模型給出的輸出y之間的差異,為了計算友善,通常情況下采用了平方關系E= 1/2 (d−y)^2 = 1/2 (d−f(x))^2 ,根據梯度下降的原則,權重的更新遵循如下規律:wj ← wi + α(d − f(x))f′(x)xi ,其中α為學習率,可以作人工調整。
四.後向傳播
對于一個多層的前饋神經網絡,我們該如何學習其中所有的參數呢?首先對于最上層的參數是非常容易獲得的,可以根據之前提到的計算模型輸出和真實輸出之間的差異,根據梯度下降的原則來得出參數結果,但問題是對于隐層來說,雖然我們可以計算出其模型輸出,但是卻不知道它的期望輸出是什麼,也就沒有辦法去高效訓練一個多層神經網絡。這也是困擾了當時學術界很長時間的一個問題,進而導緻了上個世紀六十年代之後神經網絡一直沒有得到更多發展。
後來到了十九世紀七十年代,有很多科學家獨立的提出了一個名為後向傳播的算法。這個算法的基本思想其實非常簡單,雖然在當時無法根據隐層的期望輸出去更新它的狀态,但是卻可以根據隐層對于Error的梯度來更新隐層到其他層之間的權重。計算梯度時,由于每個隐層節點與輸出層多個節點之間均有關聯,是以會對其上一層所有的Error作累加處理。
後向傳播的另一個優勢是計算同層節點的梯度和權重更新時可以并行進行,因為它們之間不存在關聯關系。整個BP算法的過程可以用如下的僞碼表示:
接下來介紹一些BP神經網絡的其他性質。BP算法其實就是一個鍊式法則,它可以非常容易地泛化到任意一個有向圖的計算上去。根據梯度函數,在大多數情況下BP神經網絡給出的隻是一個局部的最優解,而不是全局的最優解。但是從整體來看,一般情況下BP算法能夠計算出一個比較優秀的解。下圖是BP算法的直覺示範:
在大多數情況下,BP神經網絡模型會找到範圍内的一個極小值點,但是跳出這個範圍我們可能會發現一個更優的極小值點。在實際應用中針對這樣的問題我們有很多簡單但是非常有效的解決辦法,比如可以嘗試不同的随機初始化的方式。而實際上在深度學習領域當今比較常用的一些模型上,初始化的方式對于最終的結果是有非常大的影響的。另外一種使模型跳出局部最優解範圍的方式是在訓練的時候加入一些随機幹擾(Random noises),或者用一些遺傳算法去避免訓練模型停留在不理想的局部最優解位置。
BP神經網絡是機器學習的一個優秀的模型,而提到機器學習就不得不提到一個在整個機器學習過程中經常遇到的基本問題——過拟合(Overfitting)問題。過拟合的常見現象是模型在訓練集上面雖然loss一直在下降,但是實際上在test集上它的loss和error可能早已經開始上升了。避免出現過拟合問題有兩種常見的方式:
提前停止(Early Stopping):我們可以預先劃分一個驗證集(Validation),在訓練模型的同時也在驗證集之中運作這個模型,然後觀察該模型的loss,如果在驗證集中它的loss已經停止下降,這時候即使訓練集上該模型的loss仍在下降,我們依然可以提前将其停止來防止出現過拟合問題。
正則(Regularization):我們可以在神經網絡中邊的權重上加一些正則。最近幾年經常用到的dropout方式——随機丢一些點或者随機丢一些邊,也可以看作是正則的一種方式,正則也是一種很有效的防止過拟合的應用方式。
十九世紀八十年代神經網絡一度非常流行,但很不幸的是進入九十年代,神經網絡的發展又陷入了第二次低谷。造成這次低谷的原因有很多,比如支援向量機(SVM)的崛起,支援向量機在九十年代是一個非常流行的模型,它在各大會議均占有一席之地,同時也在各大應用領域都取得了非常好的成績。支援向量機有一個非常完善的統計學習理論,也有非常好的直覺解釋,并且效率也很高,結果又很理想。
是以在此消彼長的情況下,支援向量機相關的統計學習理論的崛起一定程度上壓制了神經網絡的發展熱度。另一方面,從神經網絡自身的角度來看,雖然理論上可以用BP去訓練任意程度的神經網絡,但是在實際應用中我們會發現,随着神經網絡層數的增加,神經網絡的訓練難度成幾何式增長。比如在九十年代早期,人們就已經發現在層次比較多的一個神經網絡當中可能會出現梯度消失或者梯度爆炸的一個現象。
舉一個簡單的梯度消失的例子,假設神經網絡的每一層都是一個sigmoid結構層,那麼BP向後傳播時它的loss每一次都會連成一個sigmoid的梯度。一系列的元素連接配接在一起,如果其中有一個梯度非常小的話,會導緻傳播下去的梯度越來越小。實際上,在傳播一兩層之後,這個梯度已經消失了。梯度消失會導緻深層次的參數幾乎靜止不動,很難得出有意義的參數結果。這也是為什麼多層神經網絡非常難以訓練的一個原因所在。
學術界對于這個問題有比較多的研究,最簡單的處理方式就是修改激活函數。早期的嘗試就是使用Rectified這種激活函數,由于sigmoid這個函數是指數的形式,是以很容易導緻梯度消失這種問題,而Rectified将sigmoid函數替換成max(0,x),從下圖我們可以發現,對于那些大于0的樣本點,它的梯度就是1,這樣就不會導緻梯度消失這樣一個問題,但是當樣本點處于小于0的位置時,我們可以看到它的梯度又變成了0,是以ReLU這個函數是不完善的。後續又出現了包括Leaky ReLU和Parametric Rectifier(PReLU)在内的改良函數,當樣本點x小于0時,我們可以人為的将其乘以一個比如0.01或者α這樣的系數來阻止梯度為零。
随着神經網絡的發展,後續也出現了一些從結構上解決梯度難以傳遞問題的方法,比如元模型,LSTM模型或者現在圖像分析中用到非常多的使用跨層連接配接的方式來使其梯度更容易傳播。
五.深度學習入門
經過上個世紀九十年代神經網絡的第二次低谷,到2006年,神經網絡再一次回到了大衆的視野,而這一次回歸之後的熱度遠比之前的任何一次興起時都要高。神經網絡再次興起的标志性事件就是Hinton等人在Salahudinov等地方發表的兩篇關于多層次神經網絡(現在稱作“深度學習”)的論文。
其中一篇論文解決了之前提到的神經網絡學習中初始值如何設定的問題,解決途徑簡單來說就是假設輸入值是x,那麼輸出則是解碼x,通過這種方式去學習出一個較好的初始化點。而另一篇論文提出了一個快速訓練深度神經網絡的方法。其實造成現在神經網絡熱度現狀的原因還有很多,比如當今的計算資源相比當年來說已經非常龐大,而資料也是如此。在十九世紀八十年代時期,由于缺乏大量的資料和計算資源,當時很難訓練出一個大規模的神經網絡。
神經網絡早期的崛起主要歸功于三個重要的标志性人物Hinton、Bengio和LeCun。Hinton的主要成就在于布爾計算機(Restricted Boltzmann Machine)和深度自編碼機(Deep autoencoder);Bengio的主要貢獻在于元模型在深度學習上的使用取得了一系列突破,這也是深度學習最早在實際應用中取得突破的領域,基于元模型的language modeling在2003時已經可以打敗當時最好的機率模型;LeCun的主要成就代表則是關于CNN的研究。深度學習崛起最主要的表現是在各大技術峰會比如NIPS,ICML,CVPR,ACL上占據了半壁江山,包括Google Brain,Deep Mind和FaceBook AI等在内的研究部門都把研究工作的中心放在了深度學習上面。
神經網絡進入公衆視野後的第一個突破是在語音識别領域,在使用深度學習理論之前,人們都是通過使用定義好的統計庫來訓練一些模型。在2010年,微軟采用了深度學習的神經網絡來進行語音識别,從圖中我們可以看到,兩個錯誤的名額均有将近三分之一的大幅度下降,效果顯著。而基于最新的ResNet技術,微軟公司已經把這個名額降到了6.9%,每一年都有一個明顯的提升。
到2012年,在圖檔分類領域,CNN模型在ImageNet上取得了一個較大的突破。測試圖檔分類的是一個很大的資料集,要将這些圖檔分成1000類。在使用深度學習之前,當時最好的結果是錯誤率為25.8%(2011年的一個結果),在2012年Hinton和它的學生将CNN應用于這個圖檔分類問題之後,這個名額下降了幾乎10%,自2012年之後,我們從圖表中可以觀察到每一年這個名額都有很大程度的突破,而這些結果的得出均使用了CNN模型。
深度學習模型能取得如此大的成功,在現代人看來主要歸功于其階層化的結構,能夠自主學習并将資料通過階層化結構抽象地表述出來。而抽象出來的特征可以應用于其他多種任務,這也是深度學習目前十分火熱的原因之一。
下面介紹兩個非常典型且常用的深度學習神經網絡:一個是卷積神經網絡(CNN),另外一個是循環神經網絡。
1.卷積神經網絡
卷積神經網絡有兩個基本核心概念,一個是卷積(Convolution),另一個是池化(Pooling)。講到這裡,可能有人會問,為什麼我們不簡單地直接使用前饋神經網絡,而是采用了CNN模型?舉個例子,對于一個1000*1000的圖像,神經網絡會有100萬個隐層節點,對于前饋神經網絡則需要學習10^12這樣一個龐大數量級的參數,這幾乎是無法進行學習的,因為需要海量的樣本。但實際上對于圖像來說,其中很多部分具有相同的特征,如果我們采用了CNN模型進行圖檔的分類的話,由于CNN基于卷積這個數學概念,那麼每個隐層節點隻會跟圖像中的一個局部進行連接配接并掃描其局部特征。假設每個隐層節點連接配接的局部樣本點數為10*10的話,那麼最終參數的數量會降低到100M,而當多個隐層所連接配接的局部參數可以共享時,參數的數量級更會大幅下降。
從下圖中我們可以直覺的看出前饋神經網絡和CNN之間的差別。圖中的模型從左到右依次是全連接配接的普通的前饋神經網絡,局部連接配接的前饋神經網絡和基于卷積的CNN模型網絡。我們可以觀察到基于卷積的神經網絡隐層節點之間的連接配接權重參數是可以共享的。
另一個操作則是池化(Pooling),在卷積生成隐層的基礎上CNN會形成一個中間隐層——Pooling層,其中最常見的池化方式是Max Pooling,即在所獲得的隐層節點中選擇一個最大值作為輸出,由于有多個kernel進行池化,是以我們會得到多個中間隐層節點。
那麼這樣做的好處是什麼呢?首先,通過池化操作會是參數的數量級進一步縮小;其次就是具有一定的平移不變性,如圖所示,假設圖中的九個隐層節點中的其中一個發生平移,池化操作後形成的Pooling層節點仍舊不變。
CNN的這兩個特性使得它在圖像處理領域的應用非常廣泛,現在甚至已經成為了圖像處理系統的标配。像下面這個可視化的汽車的例子就很好地說明了CNN在圖像分類領域上的應用。将原始的汽車圖檔輸入到CNN模型之中後,從起初最原始的一些簡單且粗糙的特征例如邊和點等,經過一些convolution和RELU的激活層,我們可以直覺的看到,越接近最上層的輸出圖像,其特征越接近一輛汽車的輪廓。該過程最終會得到一個隐層表示并将其接入一個全連接配接的分類層然後得出圖檔的類别,如圖中的car,truck,airplane,ship,horse等。
下圖是早期LeCun等人提出的一個用于手寫識别的神經網絡,這個網絡在九十年代時期已經成功運用到美國的郵件系統之中。感興趣的讀者可以登入LeCun的網站檢視其識别手寫體的動态過程。
當CNN在圖像領域應用十分流行的同時,在近兩年CNN在文本領域也得到了大規模應用。例如對于文本分類這個問題,目前最好的模型是基于CNN模型提出來的。從文本分類的特點來看,對一個文本的類别加以鑒别實際上隻需要對該文本中的一些關鍵詞信号加以識别,而這種工作非常适合CNN模型來完成。
實際上如今的CNN模型已經應用到人們生活中的各個領域,比如偵查探案,自動駕駛汽車的研發,Segmenttation還有Neural Style等方面。其中Neural Style是個非常有趣的應用,比如之前App Store中有個非常火的應用Prisma,可以将使用者上傳的照片轉換成其他的風格,比如轉換成梵高的星空一樣的畫風,在這其中就大量應用了CNN的技術。
2. 循環神經網絡
關于循環神經網絡的基本原理如下圖所示,從圖中可以看循環神經網絡的輸出不僅依賴于輸入x,而且依賴于目前的隐層狀态,而這個隐層狀态會根據前一個x進行更新。從展開圖中可以直覺的了解這個過程,第一次輸入的中間隐層狀态S(t-1)會影響到下一次的輸入X(t)。循環神經網絡模型的優勢在于可以用于文本、語言或者語音等此類序列型的資料,即目前資料的狀态受到此前資料狀态的影響。對于此類資料,前饋神經網絡是很難實作的。
提到RNN,那就不得不介紹一下之前提到的LSTM模型。實際上LSTM并不是一個完整的神經網絡,它隻是一個RNN網路中的節點經過複雜處理後的結果。LSTM中包含三個門:輸入門,遺忘門和輸出門。
這三個門均用于處理cell之中的資料内容,分别決定是否要将cell中的資料内容輸入、遺忘和輸出。
最後介紹一個目前非常流行的交叉領域的神經網絡的應用——将一個圖檔轉換成描述形式的文字或者該圖檔的title。具體的實作過程可以簡單的解釋為首先通過一個CNN模型将圖檔中的資訊提取出來形成一個向量表示,然後将該向量作為輸入傳送到一個訓練好的RNN模型之中得出該圖檔的描述。
直播視訊回顧位址:https://yq.aliyun.com/video/play/1370?spm=a2c41.11124528.0.0
原文釋出時間為:2018-03-25
本文作者:孫飛