boosting翻譯過來就是提升的意思,通過研究如果将許多個弱分類器內建在一起提升為一個強分類器就是多數boosting算法所研究的内容。其中最為經典的算法就是Adaboost,gdbt,xgboost等算法,本文将從xgboost的原理出發,帶大家了解boosting算法。由于xgboost是提升樹模型,是以它與決策樹是息息相關的,它通過将很多的決策樹內建起來,進而得到一個很強的分類器,xgboost中主要的思想與CART回歸樹是很類似的,是以我們先介紹一下CART決策樹,已有該部分知識的讀者可以跳過這章。
CART回歸樹
決策樹實際就是一種對空間不斷進行劃分算法,通過給每個劃分的空間賦予一個标簽或權重,那麼當樣本落到這個空間裡面,我們就認為這個樣本就滿足這個标簽。
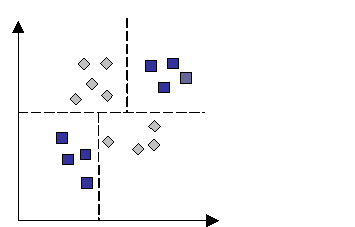
可以預見的是,對空間進行劃分其實是一個NP完全的問題,是以我們決策樹算法通常采用啟發式方法對空間進行劃分的。常用的決策樹算法有ID3,C4.5,CART決策樹。
CART決策樹又分為回歸樹和分類樹,CART回歸樹,它假設了決策樹是一顆二叉樹。它通過不斷地将特征進行分裂(劃分為左右兩半)來構造一顆決策樹。正是因為這一點,我們在使用boosting的時候,需要對離散變量進行one-hot編碼處理。你可以想象一下,将一個離散的變量劃分為兩部分其實是完全沒有意義的,因為離散的變量之間并不存在大小關系。
一個典型的CART回歸樹産生算法包含了一個目标函數:
如果我們希望對變量進行一個劃分,比如說将第j個變量x(j)和它的某個取值s劃分為兩個區域:
于是,為了求解最優的切分變量j和最優的切分點s,就轉化為求解這麼一個目标函數:
那麼我們隻需要周遊一次所有的變量的所有切分點,就可以找到一個最優的切分位置和變量。然後就這樣遞歸地往下找,就可以産生一顆回歸樹。
xgboost的建樹過程其實是與CART回歸樹類似的,有了CART回歸樹的知識,我們了解xgboost的原理也可以輕松很多。接來下将會開始進入xgboost原理的主題。
boosting介紹
boosting的核心思想就是我們希望訓練出K顆樹,将它們內建起來進而預測我們的Y。我們可以用以下公式表示:
在這裡,我們用一個函數fk(x)來表示一顆決策樹,那個函數f可以了解為将樣本x映射到樹的某個葉子結點中,樹中的每個葉子結點都會對應着一個權重w。
如圖,這就是提升樹的一個例子,這裡一共有兩顆樹,意味着我們有兩個函數f1,f2,K=2 ,然後将樣本分别放到我們的兩顆樹中,就可以計算出兩個值,把它加起來就是我們要預測的Y。
那麼我們應該如何去建立一顆樹呢?如果你了解過Adaboost,那麼可能會知道,這些樹是一顆一顆地建立起來的,通過一顆一顆地建立,不斷地減少我們的損失函數。那麼如何建立一顆樹呢?建立的時候應該怎麼去評價一次分裂的效果呢?接下來的一章将會回答這些問題。
xgboost原理
我們先來來考慮一個general的目标函數。
**
其中l是可導且凸的損失函數,用來衡量y^與y的相近程度,第二項Ω則是正則項,它包含了兩個部分,第一個是γT,這裡的T表示葉子結點的數量,γ是超參,也就是說如果γ越大,那麼我們的葉子結點數量就會越小。另外一部分則是L2正則項,通過對葉子結點的權重進行懲罰,使得不會存在權重過大的葉子結點防止過拟合。w就表示葉子結點的權重。
但是對于上面這麼一個目标函數,我們是很難進行優化的,于是我們将它變換一下,我們通過每一步增加一個基分類器ft,貪婪地去優化這個目标函數,使得每次增加,都使得loss變小。如此一來,我們就得到了一個可以用于評價目前分類器ft性能的一個評價函數:
這個算法又可以稱為前向分步優化。為了更快地去優化這個函數,我們可以在ft=0處二階泰勒展開:
其中gi表示l對f的一階偏導數
,hi表示ll對ff的二階偏導數
。由于我們的目标函數L隻受函數ff的影響,上一次的loss對本次疊代并沒有影響,于是我們可以删除掉常數項,得到:
舉個例子,假設我們的損失函數l是square loss:
那麼我們的gi和hi就等于:
由于每個ft(xi)都對應着一個葉子結點wi,于是我們可以用wi來代替一個ft,是以我們将該目标函數改寫一下可以得到:
于是,我們對wj求偏導,并令其等于0,于是就可以得到基于該目标函數的最優權重:
在實際中我們可以直接使用這裡wj的公式來計算葉子結點上的權重。
我們将最優權重回代進去,就得到我們的目标函數:
我們就可以用這個作為我們對決策樹ft性能的評分函數。但是構造決策樹實際上是一個NP問題,我們不可能周遊所有的樹結構,那麼可以用一個貪婪算法去做。它跟CART決策樹是一樣的,按照評分函數來進行貪婪搜尋。
具體步驟,先從單個葉子開始,我們設某個分裂後的屬性,将資料分為了IL,IR兩個部分,然後我們就可以計算:IL+IR−I的評分,就是我們分裂後的Gain。是以算法的基本步驟應該就是周遊所有特征的所有分割方法,選擇損失最小的,得到兩個葉子,然後繼續周遊。周遊的時候可以并行的執行。
這個公式形式上跟CART算法是一緻的,都是用分裂後的某種值 減去 分裂前的某種值,進而得到增益。為了限制樹的生長,我們可以加入門檻值,當增益大于門檻值時才讓節點分裂,上式中的gamma即門檻值,它是正則項裡葉子節點數T的系數,是以xgboost在優化目标函數的同時相當于做了預剪枝。另外,上式中還有一個系數λ,是正則項裡leaf score的L2模平方的系數,對leaf score做了平滑,也起到了防止過拟合的作用,這個是傳統GBDT裡不具備的特性。
缺失值處理
另外,基于這個分裂的評分函數,我們還可以用來處理缺失值。處理的方法就是,我們把缺失值部分額外取出來,分别放到IL和IR兩邊分别計算兩個評分,看看放到那邊的效果較好,則将缺失值放到哪部分。
建樹時的終止條件
max_depth最大樹深度:當樹達到最大深度時則停止建立決策樹。
min_child_weight:最小的樣本權重和,樣本權重和就是∑hi,當樣本權重和小于設定門檻值時則停止建樹。
将上式重寫一下我們可以得到:
我們發現hi是表示樣本權重的。
Shrinkage 與采樣
除了以上提到了正則項以外,我們還有shrinkage與列采樣技術來避免過拟合的出現。所謂shrinkage就是在每個疊代中樹中,對葉子結點乘以一個縮減權重eta。該操作的作用就是減少每顆樹的影響力,留更多的空間給後來的樹提升。
另一個技術則是采樣的技術,有兩種,一種是列采樣(colsample_bytree和colsample_bylevel),一種是行采樣(subsample)。其中列采樣的實作一般有兩種方式,一種是按層随機colsample_bylevel(一般來講這種效果會好一點),另一種是建樹前就随機選擇特征colsample_bytree。
按層随機colsample_bylevel的意思就是,上文提到每次分裂一個結點的時候,我們都要周遊所有的特征和分割點,進而确定最優的分割點,那麼如果加入了列采樣,我們會在對同一層内每個結點分裂之前,先随機選擇一部分特征,于是我們隻需要周遊這部分的特征,來确定最優的分割點。
建樹前就随機選擇特征colsample_bytree就表示我們在建樹前就随機選擇一部分特征,然後之後所有葉子結點的分裂都隻使用這部分特征。
而行采樣則是bagging的思想,每次隻抽取部分的樣本進行訓練,而不使用全部的樣本,進而增加樹的多樣性。
樣本權重
xgboost還支援設定樣本權重,這個權重展現在梯度,和二階梯度上,
也就是說樣本權重會提高或降低loss的大小。