前面一篇部落格給大家介紹了多元線性回歸的一些概念和對應的方程式的代碼實作。今天筆者再為大家介紹線性回歸的實戰演練。比如,通過空氣濕度、氣壓、風速等來預測當天的溫度。
線性回歸是對标量因變量和一個或者多個自變量之前的線性關系的模組化的最簡單,且非常強大的方法。線性回歸方程公式如下:
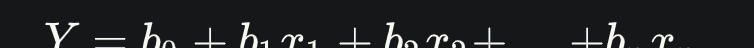
接着,我們導入天氣資料,列印天氣資料前三行,實作代碼如下:
預覽截圖如下:
檢視資料資訊:
結果如下:
檢視資料集中的分類變量:
預覽結果如下:
要預測溫度,是以需要找出資料集中不同變量之間的相關性,代碼如下:
相關性在-1到1之間變化,1表示強相關,相關系數-1表示完全負相關,相關系數為0表示變量之間不存在關系。從上圖可知,我們看到溫度與表觀溫度、濕度之間有很強的關系,也許我們還可以包括能見度。接着,我們将所有相關屬性放入一個新的資料集中并再次檢查相關性。
具體實作代碼如下所示:
現在,讓我們可視化溫度和其他因變量之間的資料,繪制溫度和濕度之間的散點圖。實作代碼如下:
預覽截圖:
圖中,濕度和溫度之間存在負相關,我們也看到了一些異常值。我們可以嘗試找到這些異常值,并将這些異常值進行删除。在統計中了解到,異常值會極大的影響線性回歸。下面,我們通過編寫一個函數來幫助我們識别資料集中濕度變量的異常值。它發現異常值的方式是基于标準差大于3。實作代碼如下所示:
接着,我們從資料集中删除這些行以獲得用于回歸的幹淨資料集。是以,我們在data_set中搜尋所有值大于0.15的濕度值并建立一個新的資料集data_set_clean。實作代碼如下:
然後,我們再來再次繪制溫度和濕度之間的資料以檢查是否還有異常值。實作代碼如下:
現在,讓我們在溫度和表觀溫度之間再畫一個散點圖,實作代碼如下:
從上圖看起來溫度和表觀溫度之間存在很強的正相關性,這也很明顯。下面,我們再繪制溫度和能見度之間的散點圖,實作代碼如下:
從圖中,我們沒有看到溫度和能見度之間有很強的關系,是以我們可以降低能見度。這裡X是我們與濕度和表觀溫度的自變量,Y是我們試圖首先學習然後計劃預測的溫度因變量。代碼如下:
列印一行X以檢視我們的自變量,代碼如下:
通過,80:20的比例将資料集拆分為訓練集和測試集,代碼如下:
我們使用sklearn庫的linear_models來拟合多元線性回歸的訓練資料,然後,從sklearn.linear_models導入庫線性回歸,并建立一個回歸對象,然後嘗試拟合訓練資料。
接着,我們列印回歸量的不同值并了解它們的含義。代碼如下:
記住線性回歸方程式,公式如下:
0.857是b1,其中x1是表觀溫度
-2.648是b2,其中x2是濕度
接着,我們找b0,代碼如下:
截圖如下:
現在,讓我們把這些數字帶入公式内進行計算,公式如下:
我們現在可以預測測試資料集的溫度,代碼如下:
那我們如何知道衡量模型的适用性呢?一個好的拟合模型是這樣一種模型,其中實際值或觀察值與基于模型的預測值之間的差異很小且無偏。是以,如果一些統計資料告訴我們實際值和預測值之間的R2可以衡量模型或回歸線對實際結果的複制程度,這是基于模型解釋的預測的總變化。
R2始終介于0和1之間或者0%到100%之間。值1表示該模型解釋了預測變量圍繞其均值的所有變化。
SSE = 實際值 - 預測值,表示與實際值相比,預測的值有多遠;
SST = 實際值 - 平均值,表示實際值與平均值相比有多遠;
SSR = 預測值 - 平均值
如果預測誤差較低,則SSE将較低且R2将接近1。這裡需要注意的是,當我們添加更多的自變量時,R2會獲得更高的值,R2值随着更多的自變量的加入而不斷增加,即使它們可能不會真正對預測産生重大影響。為了解決這個問題,我們對R2進行了調整,調整後R2會在每次添加一個無關緊要的自變量時修正該模型。
當R2接近1的值表示拟合良好。
另外,我們還可以計算均方根誤差,也稱RMSE。
RMSE顯示預測值和實際值之間的變化,由于預測值和實際值之間的差異可以是正值也可以是負值,為了抵消這種差異,我們取預測值和實際值之間的差異的平方。
找出每個觀測值的預測值和實際值之間的差異,然後将值的平方并累加:sum(預測值-實際值)2
總和除以觀察次數:sum(預測值-實際值)2/觀察次數
取第2步中的值的平方根
實作代碼如下:
接着,我們可以使用另一個庫statsmodel,代碼如下:
現在,我們使用OLS普通最小二乘法來找到最佳拟合回歸線,代碼如下:
從上圖運作結果可以看出,我們從之前的0.987值得到了一個更加好的0.997平方根值。
整個執行個體的運作代碼,如下所示:
View Code
這篇部落格就和大家分享到這裡,如果大家在研究學習的過程當中有什麼問題,可以加群進行讨論或發送郵件給我,我會盡我所能為您解答,與君共勉!
另外,部落客出書了《Kafka并不難學》和《Hadoop大資料挖掘從入門到進階實戰》,喜歡的朋友或同學, 可以在公告欄那裡點選購買連結購買部落客的書進行學習,在此感謝大家的支援。關注下面公衆号,根據提示,可免費擷取書籍的教學視訊。
<b></b><b></b><b></b><b></b>
聯系方式:
Twitter:https://twitter.com/smartloli
QQ群(Hadoop - 交流社群1):424769183
QQ群(Kafka并不難學): 825943084
溫馨提示:請大家加群的時候寫上加群理由(姓名+公司/學校),友善管理者稽核,謝謝!