To Be Continued~
總結一些優化理論的知識
假設 \(f: \mathbb{R}^n \rightarrow \mathbb{R}\),函數 \(f^*: \mathbb{R} \rightarrow \mathbb{R}\)。若兩函數滿足:
\[f^*(y) = \underset{x \in dom f}{\sup} (y^Tx-f(x))
\]
則 \(f^*\) 是 \(f\) 的共轭函數,共轭函數是使上式的上确界小于 \(\infty\) 的部分。可以了解為對于每一個确定的 \(y\),\(y^Tx\) 都是一個線性函數,此時 \(y^Tx - f(x)\) 變為線性函數與原函數在 \(x\) 的定義域上的內插補點,這個內插補點即為 \(y^Tx - f(x)\) 的值域,若此時确定的 \(y\) 不能使值域的上确界小于無窮大,則不保留,反之則保留。所有保留的 \(y\) 構成共轭函數的定義域,而所有 \(y^Tx - f(x)\) 不是 \(\infty\) 的上确界構成共轭函數的值域。
易知共轭函數是凸函數
放射函數:\(f(x) = ax +b\) 的共轭函數為:
\[f^*(y) = \sup (yx - ax -b)
觀察易得,如果 \(y \ne a\) ,那麼無論 \(y\) 取值多少,\(yx - ax -b\) 的上确界都是 \(\infty\)。但是當 \(y = a\) 時,\(yx - ax -b\) 為常數 \(-b\),上确界為 \(-b\),即此共轭函數定義域為 \(a\),值域為 \(-b\)。
負對數函數:\(f(x) = -\log x\)的共轭函數為:
\[f^*(y) = \underset{x \gt 0}{\sup} (yx + \log x)
首先\(f^*(y)^{\prime\prime} \lt 0,\) 對于某一 \(y\) 有 \(f^*(y)^{\prime} = y + \frac{1}{x} = 0\) 時,共轭函數取得最大值,此時 \(x = -\frac{1}{y}\) 使得共轭函數取得上确界,即共轭函數簡化為 \(f^*(y) = -\log(-y) - 1\)
首先解釋拉格朗日函數的形式的原因
由簡單的二維形式,并且受到等式限制的例子出發
\[\begin{aligned}
&\min f(x,y) \\
&s.t. \quad g(x,y) = c
\end{aligned}
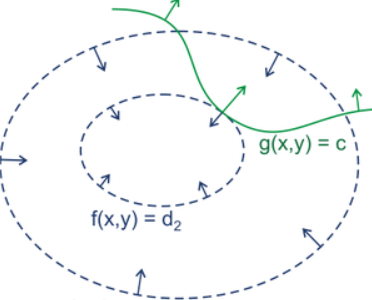
其中 \(g(x,y) = c\) 可以了解為等高線,即 \(z = g(x,y)\) 為三維曲面,當 \(z = c\) 時,可以想象為用平面 \(z = c\) 去截 \(z = g(x,y)\) 這個三維曲面所獲得的曲線,而這條曲線上滿足
\(g(x,y) = c\)。同理,如圖藍色線所示為三維曲面 \(f(x,y)\) 的各個等高線。如果沒有限制,很顯然最值會落到最小的圈裡面。正是有了限制,\(x,y\) 需要同時在藍色和綠色線上,那麼最值點就應該是兩條等高線相切的時候取得,因為如果僅僅是相交,就還在内部或者外部存在其他等高線使得取得的值更大或者更小,隻有相切的時候,可能取得最優值。
很顯然想要兩者相切必然有 \(f(x,y)\) 與 \(g(x,y)=C\) 的梯度一定是平行,則有 \(\nabla f(x,y) = \lambda (g(x,y)-C)\)。是以就容易了解當拉格朗日函數 \(F(x,y) = f(x,y) + \lambda (g(x,y) -C)\) 取得極值時就等價于兩者的梯度平行。特别地,當拉格朗日函數所有點滿足等式限制 \(g(x,y)=C\) 時兩個函數完全等價的。是以 \(F(x,y)\) 最優若等價于 \(f(x,y)\) 最優需要滿足:
\[\begin{cases}
F_x^{\prime} = 0 \\
F_y^{\prime} = 0 \\
g(x,y) = C \ \& \ \lambda \ne 0
\end{cases}
事實上,這種做法等價于利用等式限制來進行換元後,變為無限制的情況,進而按照一般的求最值來求得最優解。
那麼給出帶限制的原問題的一般形式:
&s.t. \quad m_i(x) = 0 \ (i=1,2,...,m), n_j(x) \le 0 \ (j=1,2,...,n)
即既有等式限制又有不等式限制(不等式限制,可以将其想象為一個範圍,而這個範圍依然是有邊界的,邊界就是等式限制,取得最優點一般會在邊界處),這樣可以得到拉格朗日函數
\[L(x,\lambda,\nu)=f(x)+\sum_{i=1}^m \lambda_i m_i(x) + \sum_{j=1}^n \nu_j n_j(x)
其中 $\nu_j \ge 0 $
同理,若我們想要 \(L(x,\lambda,\nu)\) 與 \(f(x)\) 同時取得最優,需要滿足等式限制,而不等式限制到達邊界(即取到等号)或者 \(\nu=0\) 已到達消除不等式限制以及使得拉格朗日函數和原函數同時取得最優的目的。總結如下
L_x^{\prime} = 0 \\
m_i(x) = 0 \ \& \ \lambda_i \ne 0 \\
\nu_j g_j(x) = 0
此時拉格朗日函數和原函數完全等價。是以進行如下推導:
\because &\sum_{j=1}^n \nu_j n_j(x) \le 0 \quad \sum_{i=1}^m \lambda_i m_i(x)=0 \\
& \max \sum_{j=1}^n \nu_j n_j(x) = 0 \\
\therefore &\underset{\nu}{\max} L(x, \nu) = f(x) \\
\therefore& \underset{x}{\min} \underset{\nu}{\max} L(x, \nu)=\underset{x}{\min} f(x)
整理一下便為 KKT 條件:
m_i(x^*) = 0 \\
\nu_j^* n_j(x^*)=0 \\
\nu_j^* \ge 0 \\
\frac{\partial L(x^*,\nu ^*)}{\partial x} = 0
弱對偶性是指:
\[\underset{x}{\min}\underset{\lambda, \nu}{\max}L(x,\lambda,\nu) \ge \underset{\lambda, \nu}{\max}\underset{x}{\min}L(x,\lambda,\nu)
這等價于證明“鳳尾”是大于“雞頭”的。證明挺簡單的如下:
\[\because \ \underset{x}{\min}L(x,\lambda,\nu) \le L(x,\lambda,\nu) \\
\therefore \ \underset{\lambda, \nu}{\max}\underset{x}{\min}L(x,\lambda,\nu) \le L(x,\lambda,\nu)
上式先變化 \(x\) 使 \(L\) 變到 \(x\) 能使其變到的最小的一個域。在這個域裡面 \(\lambda, \nu\) 是可以任意變化的,但即便 \(\lambda, \nu\) 變化使其達到最大值也隻是 \(\underset{x}{\min}L(x,\lambda,\nu)\) 的頂端了。可 \(\underset{x}{\min}L(x,\lambda,\nu)\) 整個域的所有取值可能都比 \(L(x,\lambda,\nu)\) 小,是以有 \(\underset{\lambda, \nu}{\max}\underset{x}{\min}L(x,\lambda,\nu) \le L(x,\lambda,\nu)\)
同理:
\[\because \ \underset{\lambda, \nu}{\max}L(x,\lambda,\nu) \ge L(x,\lambda,\nu) \\
\therefore \ \underset{x}{\min}\underset{\lambda, \nu}{\max}L(x,\lambda,\nu) \ge L(x,\lambda,\nu)
證畢
原問題可以簡化為隻有不等式限制的情況,因為滿足最優解的時候同樣需要滿足等式限制才能使得拉格朗日函數等于原函數。于是有:
\min f(x) \\
s.t. \ m_i(x) \le 0 \ (i = 1, 2,..., N)
于是可以得到拉格朗日函數為:
\[L(x, \lambda) = f(x) + \lambda m_i(x), \ \lambda \ge 0
此時令
p^* &= \underset{x}{\min}f(x)=\underset{x}{\min}\underset{\lambda}{\max}L(x, \lambda) \\
\ d^* &= \underset{\lambda}{\max}\underset{x}{\min}L(x, \lambda)
也就是說 $p^{*} $ 是原問題的最優解,而 \(d^{*}\) 是對偶問題的最優解。弱對偶性實際上指對偶問題的最優解是小于等于原問題的最優解的。
首先,令 \(f(x) = t,\ m_i(x) = u\),于是得到由它們不同的取值而得到一個區域,稱之為 \(G\)。定義如下:
\[G=\{(u,t)|x\in D\}
其中 \(D\) 是原問題的定義域,有了上述定義以後,便有:
\[p^* = \underset{x}{\min}f(x)=\underset{x}{\min}t=inf\{t|(u,t)\in G,u \le0\}
原問題即求 \(t\) 在 \(u \le 0\) 時的最小值。
可視化後如上圖所示,\(G\) 區域是白色區域和綠色區域的總和(即原問題的定義域),\(p^*\) 則是綠色區域 \((u \le 0)\) 的最低點(縱坐标最小的點)。此時對偶問題的最優解 \(d^*\) 轉化到 \(G\) 區域為:
d^* &= \underset{\lambda}{\max} \underset{x}{\min} L(x, \lambda) \\
&=\underset{\lambda}{\max} \underset{x}{\min} \ t+\lambda u
是以,對偶問題可以簡化為:
g(\lambda) &= \underset{x}{\min} t + \lambda u \\
&= inf\{t+\lambda u|(u,t)\in G\} \\
d^* &= g_{max}(\lambda)
對偶問題的最優解可以了解為在 \(g(\lambda)\) 的下确界中取得最大值。
可以将 \(t+\lambda_i u = b_i\) 看作一條直線,首先對于某一 \(\lambda\) ,\(b\) 由許多不同的取值 \(b_i,i=1,2,...,N\) ,可以認為是許多斜率相同,但是截距不一樣的直線(特别地,有\(\lambda \ge 0\) 是以 \(t+\lambda_i u = b_i\) 一定是斜率為負或者0的直線)。我們對于每個固定的 \(\lambda\) 取截距最小的那一條線,比如圖中的紅線,有很多條斜率與紅線相同且與 \(G\) 區域有交集的直線,但這些直線中顯然隻有與 \(G\) 區域下端相切的直線(即紅線)的截距是最小的。
于是我們得到各種不同 \(\lambda\) 中截距最小的直線,同時也得到相應的截距,如:\(b_1,b_2,b_3\) 。特别地當 \(G\) 是凹集的時候,與 \(G\) 下端有兩個切點的直線的截距是所有截距中最大的,如:黃線的 \(b_1\) 。可能有人會問為什麼不将藍線繞切點逆時針旋轉,可以獲得更大的截距,答案:不行,因為我們在獲得這些直線的時候,首先保證得是同斜率中截距最小,然後才是不同斜率中截距最大。單純将藍線旋轉,将使得藍線穿過 \(G\) 的白色區域,此時藍線不是該斜率中截距最小的。(用一條标準衡量即可:所有不同斜率的直線來比較截距大小的,必然是跟 \(G\) 的交集是一個切點或者兩個切點的直線)
此時最後篩選下來的最大截距 \(b_{max}\) 即為對偶問題的最優解 \(d^*\) ,\(d^*\) (圖中為 \(b_1\))是小于原問題的最優解 \(p^*\) 的(綠色區域中最低點的縱坐标)
如果 \(G\) 是一個凸集(即原問題為凸優化問題),那麼顯然對偶問題的最優解和原問題的最優解均為綠色區域的最低點的縱坐标,即:\(p^*=d^*\) 此時具有強對偶性,如第一列的圖和第二列的左圖(一般來說 \(G\) 為凸集,就意味着強對偶性,但也不是絕對。當然 \(G\) 不是凸集也可能具有強對偶性如:第二列的右圖。可以看得出來都是滿足 KKT 條件的,KKT 條件為求得對偶問題解和原問題解的必要條件。
定義:如果對于 \(x\) 的定義域 \(D\),如果它存在一個内點 \(x^*\) 滿足對于任意的 \(M_i(x) \lt 0\),則說明該問題滿足 slater 條件,其實也就是綠色區域部分需要有點存在。凸集加上 slater 條件即為強對偶性。