中國大學MOOC-陳越、何欽銘-資料結構-2021秋

目錄

Function

01-複雜度3 二分查找 (20 分)

02-線性結構1 兩個有序連結清單序列的合并 (15 分)

04-樹7 二叉搜尋樹的操作集 (30 分)

Programming

01-複雜度1 最大子列和問題 (20 分)

01-複雜度2 Maximum Subsequence Sum (25 分)

02-線性結構2 一進制多項式的乘法與加法運算 (20 分)

02-線性結構3 Reversing Linked List (25 分)

02-線性結構4 Pop Sequence (25 分)

03-樹1 樹的同構 (25 分)

04-樹4 是否同一棵二叉搜尋樹 (25 分)

05-樹7 堆中的路徑 (25 分)

05-樹8 File Transfer (25 分)

本題要求實作二分查找算法。

思路：

想一想這個說法是否正确？在二分查找的程式實作中，如果left和right的更新不是取mid+1和mid-1而是都取mid，程式也是正确的。

答案

這個說法是錯誤的 。

考慮查找值大于數組内最大值的情況，如果都取mid，循環到隻有兩元素時就會導緻mid始終與左邊界值相等，進而程式**無限循環**；考慮查找值小于數組内最小值的情況，由于可能存在數列中僅有一個元素的情況是以進入循環的條件必須要包含left==right，在此前提下，循環到最後左右邊界與mid将會重合進而無限循環。

本題要求實作一個函數，将兩個連結清單表示的遞增整數序列合并為一個非遞減的整數序列。

思路：注意非遞減的意思是，不嚴格遞增。也就是說，當遇到兩個相同的數字時，兩個數字都要合并進去。

完成日期：21.11.06

本題要求實作給定二叉搜尋樹的5種常用操作。

函數接口定義：

其中<code>BinTree</code>結構定義如下：

函數<code>Insert</code>将<code>X</code>插入二叉搜尋樹<code>BST</code>并傳回結果樹的根結點指針；

函數<code>Delete</code>将<code>X</code>從二叉搜尋樹<code>BST</code>中删除，并傳回結果樹的根結點指針；如果<code>X</code>不在樹中，則列印一行<code>Not Found</code>并傳回原樹的根結點指針；

函數<code>Find</code>在二叉搜尋樹<code>BST</code>中找到<code>X</code>，傳回該結點的指針；如果找不到則傳回空指針；

函數<code>FindMin</code>傳回二叉搜尋樹<code>BST</code>中最小元結點的指針；

函數<code>FindMax</code>傳回二叉搜尋樹<code>BST</code>中最大元結點的指針。

裁判測試程式樣例：

輸入樣例：

輸出樣例：

AC code：

根據搜尋二叉樹左小右大的特點設定函數。

時常利用遞歸。

多考慮樹節點為空的情況。

本地AC code：

給定K個整數組成的序列{ N1, N2, ..., NK }，“連續子列”被定義為{ Ni, Ni+1, ..., Nj }，其中 1≤i≤j≤K。“最大子列和”則被定義為所有連續子列元素的和中最大者。例如給定序列{ -2, 11, -4, 13, -5, -2 }，其連續子列{ 11, -4, 13 }有最大的和20。現要求你編寫程式，計算給定整數序列的最大子列和。

本題旨在測試各種不同的算法在各種資料情況下的表現。各組測試資料特點如下：

資料1：與樣例等價，測試基本正确性；

資料2：10^2個随機整數；

資料3：10^3個随機整數；

資料4：10^4個随機整數；

資料5：10^5個随機整數；

輸入格式:

輸入分2行，每行分别先給出多項式非零項的個數，再以指數遞降方式輸入一個多項式非零項系數和指數（絕對值均為不超過1000的整數）。數字間以空格分隔。

輸出格式:

輸出分2行，分别以指數遞降方式輸出乘積多項式以及和多項式非零項的系數和指數。數字間以空格分隔，但結尾不能有多餘空格。零多項式應輸出<code>0 0</code>。

輸入樣例:

輸出樣例:

答案：

思路：用數組實作，<code>MaxSubseqSum2</code>使用兩個for循環，比較目前子列和與預設最大子列和。

Given a sequence of K integers { N1, N2, ..., NK }. A continuous subsequence is defined to be { Ni, Ni+1, ..., Nj } where 1≤i≤j≤K. The Maximum Subsequence is the continuous subsequence which has the largest sum of its elements. For example, given sequence { -2, 11, -4, 13, -5, -2 }, its maximum subsequence is { 11, -4, 13 } with the largest sum being 20.

Now you are supposed to find the largest sum, together with the first and the last numbers of the maximum subsequence.

Input Specification:

Each input file contains one test case. Each case occupies two lines. The first line contains a positive integer K (≤10000). The second line contains K numbers, separated by a space.

Output Specification:

For each test case, output in one line the largest sum, together with the first and the last numbers of the maximum subsequence. The numbers must be separated by one space, but there must be no extra space at the end of a line. In case that the maximum subsequence is not unique, output the one with the smallest indices i and j (as shown by the sample case). If all the K numbers are negative, then its maximum sum is defined to be 0, and you are supposed to output the first and the last numbers of the whole sequence.

Sample Input:

Sample Output:

AC code:

Reference AC code:

思路：要區分兩種特殊情況。

至少有一個零，輸出結果為 <code>0 0 0</code>

全都是負數，輸出結果為 <code>0 first_neg_number last_neg_number</code>

設計函數分别求兩個一進制多項式的乘積與和。

注意：

1、<code>P(front)</code>作為頭部空結點指針，最後<code>P(front)</code>要用<code>t</code>配合<code>free</code>函數釋放。

2、<code>rear = P(front)</code> 一開始是空結點指針，但最後會作為尾部結點指針，是以最終<code>rear-&gt;link == NULL</code>

3、設定<code>flag</code>調整輸出格式。

Given a constant K and a singly linked list L, you are supposed to reverse the links of every K elements on L. For example, given L being 1→2→3→4→5→6, if K=3, then you must output 3→2→1→6→5→4; if K=4, you must output 4→3→2→1→5→6.

翻譯：給定一個常數K和一個單鍊連結清單L，你應該把L上每個K元素的鍊結颠倒。例如，給定L為1→2→3→4→5→6，如果K=3，那麼你必須輸出3→2→1→6→5→4；如果K=4，你必須輸出4→3→2→1→5→6。

Each input file contains one test case. For each case, the first line contains the address of the first node, a positive N (≤105) which is the total number of nodes, and a positive K (≤N) which is the length of the sublist to be reversed. The address of a node is a 5-digit nonnegative integer, and NULL is represented by -1.

翻譯：每個輸入檔案包含一個測試用例。對于每種情況，第一行包含第一個節點的位址、節點總數的正N（&lt;105）和要反轉的子清單的長度的正K（&lt;N）。節點的位址是一個5位非負整數，空值用-1表示。

Then N lines follow, each describes a node in the format:

where <code>Address</code> is the position of the node, <code>Data</code> is an integer, and <code>Next</code> is the position of the next node.

For each case, output the resulting ordered linked list. Each node occupies a line, and is printed in the same format as in the input.

思路：用三個數組的方式模拟連結清單，分别存放目前位址、數值、下一個位址。實際上用結構數組、連結清單的方法也可以，但三個數組易于了解。

樣例圖示：

參考連結1；參考連結2

完成日期：21.11.07

Given a stack which can keep M numbers at most. Push N numbers in the order of 1, 2, 3, ..., N and pop randomly. You are supposed to tell if a given sequence of numbers is a possible pop sequence of the stack. For example, if M is 5 and N is 7, we can obtain 1, 2, 3, 4, 5, 6, 7 from the stack, but not 3, 2, 1, 7, 5, 6, 4.

Each input file contains one test case. For each case, the first line contains 3 numbers (all no more than 1000): M (the maximum capacity of the stack), N (the length of push sequence), and K (the number of pop sequences to be checked). Then K lines follow, each contains a pop sequence of N numbers. All the numbers in a line are separated by a space.

For each pop sequence, print in one line "YES" if it is indeed a possible pop sequence of the stack, or "NO" if not.

翻譯：

給定一個最多能儲存M個數的堆棧。按1，2，3，…，N的順序推N個數字，然後随機彈出。您應該知道給定的數字序列是否可能是堆棧的彈出序列。例如，如果M是5，N是7，我們可以從堆棧中獲得1，2，3，4，5，6，7，但不能從3，2，1，7，5，6，4。

輸入規格：

每個輸入檔案包含一個測試用例。對于每種情況，第一行包含3個數字（都不超過1000）：M（堆棧的最大容量）、N（推送序列的長度）和K（要檢查的pop序列的數量）。接下來是K行，每行包含N個數字的pop序列。一行中的所有數字都用空格隔開。

輸出規格：

對于每個彈出序列，如果确實是堆棧的可能彈出序列，則在一行中列印 "YES"，如果不是，則列印"NO"。

pop randomly這句話要和堆棧先進後出的特點緊密聯系。

按1，2，3....，N（正整數序列）依次入棧，每入棧一個元素都要先判斷是否溢出，如果沒溢出，再判斷該元素能否出棧及其之前已經入棧的元素能否出棧。最後，如果樣例所有元素都能出棧，則說明是出棧序列。

參考連結

給定兩棵樹T1和T2。如果T1可以通過若幹次左右孩子互換就變成T2，則我們稱兩棵樹是“同構”的。例如圖1給出的兩棵樹就是同構的，因為我們把其中一棵樹的結點A、B、G的左右孩子互換後，就得到另外一棵樹。而圖2就不是同構的。

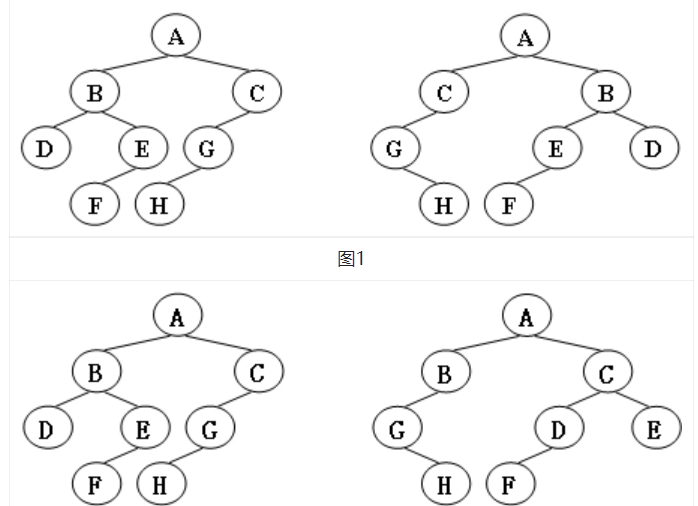
現給定兩棵樹，請你判斷它們是否是同構的。

輸入給出2棵二叉樹樹的資訊。對于每棵樹，首先在一行中給出一個非負整數N (≤10)，即該樹的結點數（此時假設結點從0到N−1編号）；随後N行，第i行對應編号第i個結點，給出該結點中存儲的1個英文大寫字母、其左孩子結點的編号、右孩子結點的編号。如果孩子結點為空，則在相應位置上給出“-”。給出的資料間用一個空格分隔。注意：題目保證每個結點中存儲的字母是不同的。

如果兩棵樹是同構的，輸出“Yes”，否則輸出“No”。

輸入樣例1（對應圖1）：

輸出樣例1:

輸入樣例2（對應圖2）：

輸出樣例2:

判斷cl、cr是否為橫杠<code>-</code>時，四個if語句是處于同一水準同時判斷的。

初始化root為Null可以使得當N為空時，能夠傳回Null(-1)。

判斷是否“同構”時，需要多方考慮。也要經常調用遞歸。

給定一個插入序列就可以唯一确定一棵二叉搜尋樹。然而，一棵給定的二叉搜尋樹卻可以由多種不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始為空的二叉搜尋樹，都得到一樣的結果。于是對于輸入的各種插入序列，你需要判斷它們是否能生成一樣的二叉搜尋樹。

輸入包含若幹組測試資料。每組資料的第1行給出兩個正整數N (≤10)和L，分别是每個序列插入元素的個數和需要檢查的序列個數。第2行給出N個以空格分隔的正整數，作為初始插入序列。随後L行，每行給出N個插入的元素，屬于L個需要檢查的序列。

簡單起見，我們保證每個插入序列都是1到N的一個排列。當讀到N為0時，标志輸入結束，這組資料不要處理。

對每一組需要檢查的序列，如果其生成的二叉搜尋樹跟對應的初始序列生成的一樣，輸出“Yes”，否則輸出“No”。

兩個flag要區分開，<code>Check</code>的flag是要用來标記是否已經檢查過，不要重複檢查

<code>Judge</code>的flag是用來标記兩棵樹是否已經一緻

除了對照樹要當作樹來建立，目标樹當作序列對待即可，這也是<code>Check</code>設定flag的原因

b站參考連結

将一系列給定數字插入一個初始為空的小頂堆<code>H[]</code>。随後對任意給定的下标<code>i</code>，列印從<code>H[i]</code>到根結點的路徑。

每組測試第1行包含2個正整數N和M(≤1000)，分别是插入元素的個數、以及需要列印的路徑條數。下一行給出區間[-10000, 10000]内的N個要被插入一個初始為空的小頂堆的整數。最後一行給出M個下标。

對輸入中給出的每個下标<code>i</code>，在一行中輸出從<code>H[i]</code>到根結點的路徑上的資料。數字間以1個空格分隔，行末不得有多餘空格。

思路：先丢個連結，何欽銘老師的思路。

We have a network of computers and a list of bi-directional connections. Each of these connections allows a file transfer from one computer to another. Is it possible to send a file from any computer on the network to any other?

Each input file contains one test case. For each test case, the first line contains N (2≤N≤104), the total number of computers in a network. Each computer in the network is then represented by a positive integer between 1 and N. Then in the following lines, the input is given in the format:

where <code>I</code> stands for inputting a connection between <code>c1</code> and <code>c2</code>; or

where <code>C</code> stands for checking if it is possible to transfer files between <code>c1</code> and <code>c2</code>; or

where <code>S</code> stands for stopping this case.

For each <code>C</code> case, print in one line the word "yes" or "no" if it is possible or impossible to transfer files between <code>c1</code> and <code>c2</code>, respectively. At the end of each case, print in one line "The network is connected." if there is a path between any pair of computers; or "There are <code>k</code> components." where <code>k</code> is the number of connected components in this network.

Sample Input 1:

Sample Output 1:

Sample Input 2:

Sample Output 2:

思路：先丢個連結，陳越老師的思路。