這篇文章提出了一個利用社交網絡資訊的推薦模型SamWalker。SamWalker可以模組化使用者和物品之間的曝光機率,并提出用社交網絡随機遊走進行負采樣的方式來替代曝光機率的計算,降低模型計算複雜度。此外,模型還可以利用等效的卷積神經網絡來優化社交連接配接強度。在三個資料集上,SamWalker都取得了超過所有baseline的性能,并結合Ablation study等實驗證明了模型的性能。
Authors: Jiawei Chen, Can Wang, Sheng Zhou, Qihao Shi, Yan Feng, Chun Chen
WWW'19 浙江大學
論文連結:https://zhoushengisnoob.github.io/papers/SamWalker.pdf
目錄
SamWalker: Social Recommendation with Informative Sampling Strategy
0. 總結
1. 研究目标
2. 問題背景
3. 方法
3.1 問題定義
3.2 EXMF分析
3.3 SamWalker 概述
3.4 基于随機遊走的個性化負采樣方法
3.5 社交連接配接強度的優化
3.6 方法讨論
4. 實驗
4.1 資料集
4.2 推薦性能
4.3 采樣器性能
4.4 Ablation study
4.5 對模型性能的影響
5. 不懂的問題
6. 進一步閱讀
利用社交資訊模組化曝光機率,提高推薦準确率和模型穩定性。
在隐式回報資料中,一個使用者沒有與一個物品發生互動,可能是因為使用者對物品沒有興趣,也可能是因為使用者沒有看到這個物品。是以,将所有未觀測到的互動都作為負樣本進行采樣,會損害推薦系統的性能,這也被稱為推薦系統中的exposure bias。現有的方法通過對未觀測資料進行降級來緩解exposure bias,但這些方法存在兩個問題:(1)權重通常是人工賦予的,缺乏靈活性和準确性。(2)資料中包含的資訊很少,難以準确預測曝光機率。
為了解決上述問題,本文提出了SamWalker,利用社交資訊來推斷曝光機率,并指導采樣過程。
使用者會從朋友/關注的人那裡獲得有關物品的資訊(例如朋友之間的推薦),是以,使用者的社交資訊會影響物品對使用者的曝光機率。一個物品在使用者的社交網絡中越流行,使用者看到這個物品的機率就越高。
由于社交網絡很複雜,基于社交網絡計算所有user-item對的曝光機率複雜度很高。本文采用在社交網絡上随機遊走的方式指導負采樣。
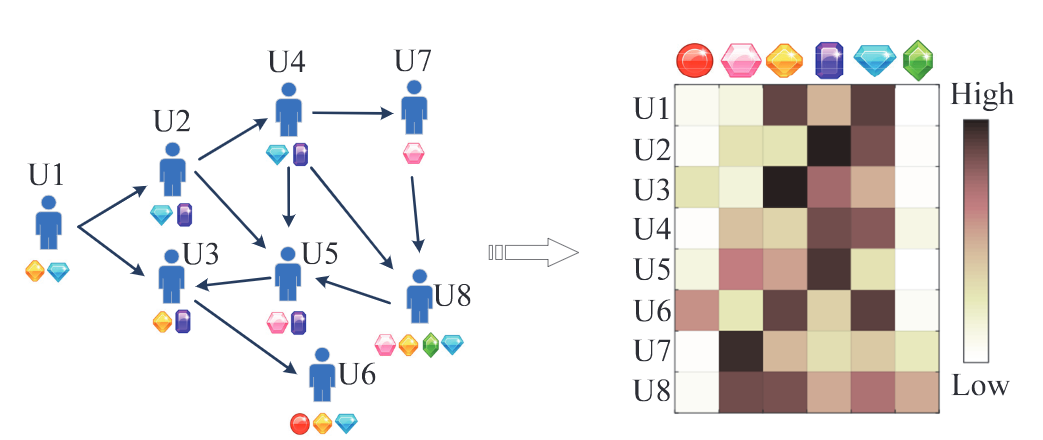
假設我們有使用者集U,包含n個使用者;物品集I,包含m個物品;隐式回報互動記錄X,矩陣次元為\(n*m\),其中每個元素\(x_{ij}\)表示使用者i與物品j是否發生了互動(1或0);社交資訊矩陣T,矩陣次元為\(n*n\),其中每行元素\(\tau_i\)表示使用者i的社交連結,\(\tau_{ij}\)表示使用者i與使用者j是否有社交聯系。
EXMF是2016年提出的模組化曝光機率的推薦模型,具體請參考博文【論文筆記】Modeling User Exposure in Recommendation。
(3.3變分分析這部分我還沒看明白,等後面懂了再來寫詳細過程orz)
EXMF的缺點
EXMF模組化曝光機率的參數過多(m*n),工業場景下不可實作;且大部分曝光機率都很小,對模型優化貢獻很小。
EXMF認為曝光機率與使用者的特征無關,但實際上使用者的社交網絡對曝光機率也有着極大的影響。
為了降低參數量,使用一個傳播模型來模組化社交資訊對曝光機率的影響,從第t步到第t+1步的曝光機率傳播方式如下:
\[\begin{align}
\gamma_{i j}^{(t+1)}=(1-c) x_{i j}+\sum_{k \in \mathcal{T}_{i}} c \varphi_{i k} \gamma_{k j}^{(t)}
\end{align}
\]
其中i表示使用者i,j表示物品j,\(\gamma_{i j}^{(t+1)}\)表示第t+1步的曝光機率,\(x_{ij}\)表示訓練集的标簽(0或1,表示是否互動),\(\varphi_{i k}\)表示使用者i和使用者k之間的連接配接強度,滿足\(\sum_{k\in\tau_i}\varphi_{ik} = 1\),c是調節社交資訊權重的參數。
總的來說,曝光機率收斂公式為:
Y=g_{\varphi}(X, T) \equiv \lim _{t \rightarrow \infty} Y^{(t)}=(I-c \Phi)^{-1}(1-c) X
\(Y^{(t)}_{ij}\) = \(\gamma_{i j}^{(t)}\),是第t步的曝光機率矩陣;\(\phi_{ij} = \varphi_{ij}\),是社交連接配接強度矩陣 。
作者證明了當采樣機率\(p_{ij}\)正比于曝光機率\(\gamma_{i j}^{(t)}\)時,采樣方差更小,且梯度估計更快(就是用負采樣階段的設計來替代loss函數中的曝光機率計算)。
那怎樣能夠做到正比于曝光機率\(\gamma_{i j}^{(t)}\)的負采樣呢?
一個直覺的想法就是計算出所有的曝光機率,再進行負采樣,但這樣計算複雜度太高。
曝光機率的計算疊代公式可以展開為:
\[\begin{aligned}
Y &=(I-c \Phi)^{-1}(1-c) X \\
&=\left(1+c \Phi+(c \Phi)^{2}+(c \Phi)^{3} \ldots\right)(1-c) X
\end{aligned}
基于上式,對于user i,我們給出如下随機遊走規則進行負采樣,使得負采樣機率正比于推導出的曝光機率:
在第t步随機遊走時,假設我們遊走到了user u。
我們有兩種選擇:
(1)這一步不進行遊走,随機選擇u的一定比例(\(\beta\))的鄰居物品i作為負樣本。機率為c。
(2)根據社交連接配接強度\(\varphi_{uv}\)進行随機遊走,遊走至使用者節點v,并随機選擇v的一定比例(\(\beta\))的鄰居物品i作為負樣本。機率為(1-c)。
直至遊走\(\alpha\)步,随機遊走結束,負采樣結束。
在每次随機遊走過程中,如果遊走到距離很遠的user,社交資訊就變得很少了。具體來說,如果目前節點與初始節點i的距離\(t>t_m\),則直接在所有user中随機選擇,進行遊走。
由于不同的社交連接配接對使用者的影響是不同的,例如由于朋友之間聯系的密切程度不同,朋友之間的推薦頻率和推薦強度也不同。而曝光機率\(\gamma_{i j}^{(t)}\)的推導是基于社交連接配接強度矩陣的,而這個矩陣需要我們進行優化。
為了優化連接配接強度,設計一個卷積神經網絡來計算曝光機率,網絡中的權重就是user之間的連接配接強度。這樣可以在優化推薦loss的時候回傳梯度,達到優化連接配接強度的目的。
由于使用者不僅會受到直接好友的影響,還會受到大衆輿論的影響。是以,可以在模型中加入一個節點,代表所有使用者對一個使用者行為的影響。随機遊走的設計也需要做出響應改變,即增加一個直接在所有使用者中随機選擇節點的機率。
實驗采用了Epinions、Ciao和LastFM三個資料集。其中Epinions和Ciao是從産品評論網站抓取的資訊,含有使用者之間的“信任”資訊;LastFM是從音樂網站爬取的,含有使用者之間的好友資料。
實驗結果表明,在三個資料集上,SamWalker都優于所有baseline。
實驗結果表明,SamWalker設計的社交網絡随機遊走采樣器可以降低梯度的方差,獲得更穩定的模型。
實驗表明,學習個性化的連接配接強度、引入社交資訊和全局社交資訊都有助于提升模型性能。圖中SamWalker-ho表示所有社交連接配接強度都是一樣的;SamWalker-l表示隻考慮社交資訊,不考慮全局user;SamWalker-g表示隻考慮全局user,不考慮社交資訊。
\(t_m\)表示随機遊走的最大長度,當随機遊走超過此長度時,會在所有使用者中随機選擇節點進行遊走。
随着\(t_m\)的增加,性能呈現先上升後下降的特點。在\(t_m\)比較小的時候,增加\(t_m\)可以提供更廣的社交資訊。但随着\(t_m\)的進一步增大,帶來的有用社交資訊開始減少,噪聲開始增多,模型性能會開始出現下降。實際上,在社交網絡中,從一個節點出發,6跳就可以基本覆寫所有人,是以過長的随機遊走效果不好。
變分法
[5] Rocío Cañamares and Pablo Castells. 2018. Should i follow the crowd?: A probabilistic analysis of the effectiveness of popularity in recommender systems. In The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval. ACM, 415–424
[6]Pablo Castells, Neil J Hurley, and Saul Vargas. 2015. Novelty and diversity in recommender systems. In Recommender Systems Handbook. Springer, 881–918.
[12]Jingtao Ding, Fuli Feng, Xiangnan He, Guanghui Yu, Yong Li, and Depeng Jin. 2018. An improved sampler for bayesian personalized ranking by leveraging view data. In Companion of the The Web Conference 2018 on The Web Conference 2018. International World Wide Web Conferences Steering Committee, 13–14.
[17]Xiangnan He, Lizi Liao, Hanwang Zhang, Liqiang Nie, Xia Hu, and Tat-Seng Chua. 2017. Neural collaborative filtering. In Proceedings of the 26th International Conference on World Wide Web. International World Wide Web Conferences Steering Committee, 173–182.
[18]Xiangnan He, Hanwang Zhang, Min-Yen Kan, and Tat-Seng Chua. 2016. Fast matrix factorization for online recommendation with implicit feedback. In Proceedings of the 39th International ACM SIGIR conference on Research and Development in Information Retrieval. ACM, 549–558.
[26]Chen Jiawei, Feng Yan, Ester Martin, Zhou Sheng, Chen Chun, and Can Wang. 2018. Modeling Users’ Exposure with Social Knowledge Influence and Consumption Influence for Recommendation. In Proceedings of the 27th ACM International on Conference on Information and Knowledge Management. ACM, 953–962
本文連結:https://www.cnblogs.com/zihaojun/p/15703157.html
本文來自部落格園,作者:子豪君,轉載請注明原文連結:https://www.cnblogs.com/zihaojun/p/15703157.html