【論文筆記】Recommendations as Treatments: Debiasing Learning and Evaluation

Authors: Tobias Schnabel, Adith Swaminathan, Ashudeep Singh, Navin Chandak, Thorsten Joachims

ICML’16 Cornell University

目錄

Recommendations as Treatments: Debiasing Learning and Evaluation

0. 總結

1.研究目标

2.問題背景

3. IPS評價名額

3.1 任務1：評分預測準确率評價

3.2 推薦品質評價

3.3 基于傾向分數的性能評估

3.4 實驗驗證

4. IPS推薦系統

5. 傾向性評分的估計

6. 實驗

6.1 實驗設定

6.2 采樣偏差對評測名額的影響

6.3 采樣偏差對模型訓練的影響

6.4 傾向性評分估計準确度的影響

6.5 真實資料集上的性能

本文提出了基于IPS的評測名額和模型訓練方法，并提出了兩種傾向性評分的估計方法。收集并公開了Coat資料集，在半合成資料集和無偏資料集上，驗證了評測名額對Propensity score估計的魯棒性和IPS-MF的性能優越性。

去除選擇偏差（selection-bias）對模型性能評測（evaluation）和模型訓練（training）帶來的不利影響。

推薦系統中的選擇偏差（selection bias）可能有兩個來源：首先，使用者更可能跟自己感興趣的物品發生互動，不感興趣的物品更可能沒有互動記錄；第二，推薦系統在給出推薦清單時也會傾向于給使用者推薦符合使用者興趣的産品。

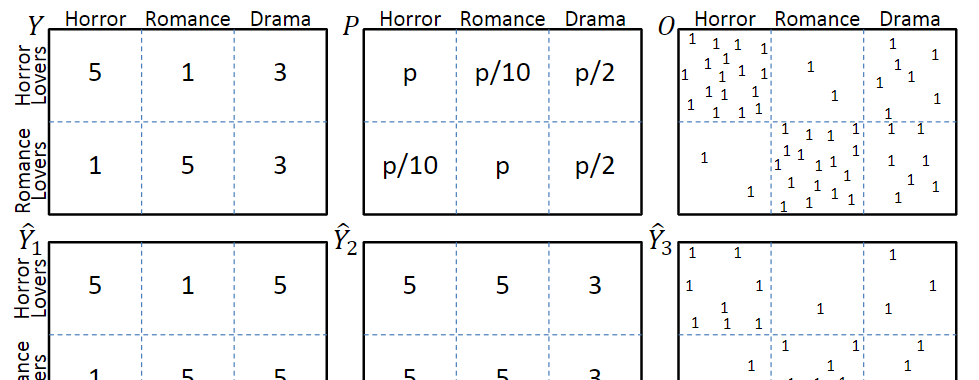
圖一

考慮圖一中的模型，圖中第一行分别表示真實評分Y、曝光機率P和曝光分布O，其中評分越低的互動，觀測到的機率也就越低。第二行\(\hat{Y}_1\)和\(\hat{Y}_2\)分别表示兩種不同的預測結果，\(\hat{Y}_3\)表示是否發生了互動。

在理想情況下，即所有評分都被觀測到時，評價名額為

\[R(\hat{Y})=\frac{1}{U \cdot I} \sum_{u=1}^{U} \sum_{i=1}^{I} \delta_{u, i}(Y, \hat{Y})

\]

但在存在selection bias的場景下，評價名額會變為

\[\hat{R}_{n a i v e}(\hat{Y})=\frac{1}{\left|\left\{(u, i): O_{u, i}=1\right\}\right|} \sum_{(u, i): O_{u, i}=1} \delta_{u, i}(Y, \hat{Y})

從喜惡判斷的角度，\(\hat{Y}_1\)明顯優于\(\hat{Y}_2\)；但是從評價名額上看，由于\(\hat{Y}_2\)中預測錯誤的那些互動很少被觀測到，是以，\(\hat{Y}_2\)會優于\(\hat{Y}_1\)。

評價推薦結果的品質，也就是在回答一個反事實問題：如果使用者與推薦清單中的物品發生互動，而不是實際上的互動曆史，使用者的體驗會得到多大程度的提升？

評價名額可以是DCG等。由于觀測資料是有偏的，與3.1中的描述相似，最終的評價名額也是有偏的。

解決selection bias的關鍵在于了解觀測資料的生成機制（Assignment Mechanism），包含系統生成（Experimental Setting）和使用者選擇（Observational Setting）兩種因素。

為了解決評測名額的偏差問題，作者提出使用逆傾向分數對觀察資料權重，建構一個對理想評測名額的無偏估計器——IPS Estimator：

\[\hat{R}_{I P S}(\hat{Y} | P)=\frac{1}{U \cdot I} \sum_{(u, i): O_{u, i}=1} \frac{\delta_{u, i}(Y, \hat{Y})}{P_{u, i}}\\

\mathbb{E}_{O}\left[\hat{R}_{I P S}(\hat{Y} | P)\right] =\frac{1}{U \cdot I} \sum_{u} \sum_{i} \mathbb{E}_{O_{u, i}}\left[\frac{\delta_{u, i}(Y, \hat{Y})}{P_{u, i}} O_{u, i}\right] \\

=\frac{1}{U \cdot I} \sum_{u} \sum_{i} \delta_{u, i}(Y, \hat{Y})=R(\hat{Y})

其中\(O_{u,i} ~ Bernoulli(P_{u,i})\)，\(P_{u,i}\)為propensity score。

利用MF生成的全曝光模拟資料集，作者設計了幾種評分政策，每種政策都有不同的評分錯誤。基于真實資料集中的曝光情況，計算曝光互動的評價名額，證明了IPS評價名額能有效抵消selection bias帶來的評價誤差。

基于IPS的推薦系統，訓練目标為：

\[\underset{V, W, A}{\operatorname{argmin}}\left[\sum_{O_{u, i}=1} \frac{\delta_{u, i}\left(Y, V^{T} W+A\right)}{P_{u, i}}+\lambda\left(\|V\|_{F}^{2}+\|W\|_{F}^{2}\right)\right]

其中\(P_{u,i}\)是傾向性評分，相當于在對應的loss項上加了權重。

作者提出了兩種估計方法

樸素貝葉斯估計

這個方法似乎是對評分相同的u-i互動給出了相同的評分？

\[P\left(O_{u, i}=1 \mid Y_{u, i}=r\right)=\frac{P(Y=r \mid O=1) P(O=1)}{P(Y=r)}

邏輯斯特回歸

将所有關于u-i對的資訊都作為特征，來學習一個線性模型

\[P_{u, i}=\sigma\left(w^{T} X_{u, i}+\beta_{i}+\gamma_{u}\right)

訓練集是有偏（MNAR）資料，使用k-折交叉驗證來調參，使用無偏資料或者合成的全曝光資料作為測試集。

建構全曝光的合成資料集：在ML 100K資料集上，使用MF 填充所有空缺的評分，并對填充之後的評分分布進行調整，以降低高評分的比例。

實驗結果見3.4

對于不同程度的選擇偏差（\(\alpha\)越小，選擇偏差越大)，實驗結果如下圖。

可見，IPS-MF和SNIPS-MF的性能要明顯優于naive-MF。

使用不同比例的資料來估計傾向性評分，可以看出，在所有條件下，IPS和SNIPS都優于MF，驗證了模型對傾向性評分的魯棒性。

Yahoo! R3：使用5%的無偏資料來估計傾向性評分，95%的無偏資料作為測試集。

Coat：本文收集了一個新的無偏資料集Coat（很大的貢獻），包含290個user和300個item，每個user自主選擇24個商品給出評分，并對16個随機商品給出評分（1-5分）。

實驗結果表明，在兩個資料集上都優于最好的baseline。

本文來自部落格園，作者：子豪君，轉載請注明原文連結：https://www.cnblogs.com/zihaojun/p/15665756.html