1 問題描述
何為Kruskal算法?
該算法功能:求取權重連通圖的最小生成樹。假設權重連通圖有n個頂點,那麼其最小生成樹有且僅有n - 1條邊。
該算法核心思想:從給定權重連通圖中,選擇目前未被選擇的,不能形成回路且權值最小的邊,加入到目前正在構造的最小生成樹中。
2 解決方案
2.1 構造最小生成樹示例
下面請看一個具體示例:
給定一個權重連通圖,其包含5個頂點,分别為:1,2,3,4,5。包含7條邊,按照從小到大排序依次為:
1-2,5
2-3,5
3-5,6
2-4,12
4-5,12
2-5,15
3-4,17
那麼可知,使用kruskal算法構造該權重連通圖的最小生成樹,則需要選擇出這7條邊中滿足定義的4條邊。
(1)原始圖
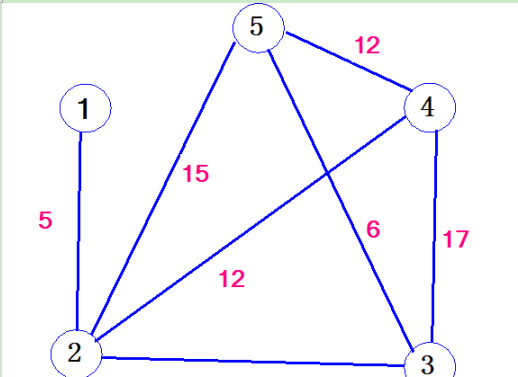
(2)添加第1條邊
此時未選中任何一條邊,那麼直接選擇7條邊中最小的一條邊,2-3,5。(PS:當權值最小的邊有多個時,隻要滿足定義,可以随意選擇一條邊即可。例如,此處也可以選擇1-2,5)
(2)添加第2條邊
此時,從剩餘的6條邊中選擇最小權值的邊,可以輕易知道為1-2,5。加入此邊後,檢查此時的正在構造的最小生成樹,沒有回路,符合定義,即可以确認加入。
(3)添加第3條邊
此時,從剩餘的5條邊中選擇最小權值且不會生成環的邊,輕易可知,3-5,6符合要求。
(4)添加第4條邊(PS:此時也是最小生成樹的最後一條邊)
從剩餘的4條邊中選擇最小權值且不會生成回環的邊,發現2-4,12、4-5,12均符合要求,此時,任意選擇其中一條邊即可。這裡,我選擇的是4-5,12。
(5)最小生成樹以及構造完畢,結束構造。
2.2 僞碼及時間效率分析
該算法在開始的時候,會将給定連通圖所有邊的權值進行從小到大排列。然後,從一個空子圖開始,它會掃描這個這個有序清單,并試圖把清單中的下一條邊加入到目前正在構造的子圖(或者說是最小生成樹)中。目前,這種添加不能形成一個回路,如果産生了回路,則把這條邊跳過。
通過以上的僞碼,可以知道,Kruskal算法的時間效率取決于兩點:
(1)對給定連通圖所有邊權值進行排序的時間效率;
(2)對新加入邊,進行是否形成回路判斷的時間效率。
首先,談談(1)的時間效率。對于排序算法,一般的時間效率分為O(n^2)(例如,選擇排序和冒泡排序)和O(nlogn)(例如,合并排序和快速排序)。由于合并排序,相對于快速排序要穩定,是以,此處我們可以選擇合并排序來處理問題(1),即時間效率為O(nlogn),其中n為頂點總數。
其次,談談(2)的時間效率。對于問題(2)中要實作的功能,有一些高效的算法可以實作這種功能,這些算法的核心就是對兩個頂點是否屬于同一棵樹的關鍵性檢查,它們被稱為并查算法,而該算法能夠達到的最優時間效率為O(eloge),其中e為具體邊總數。
最後,我們來探讨一下使用并查算法實作(2)中要求的功能。
使用并查算法實作檢查回環問題,這裡涉及的是一種抽象資料類型,這種資料類型是由某個有限集的一系列不相交子集以及下面這些操作構成的。
id(x)生成一個單元集合{x}。假設這個操作對集合S的每一個元素隻能應用一次。
find(x)傳回一個包含x的子集。
union(x, y)構造分别包含x和y的不相交子集Sx和Sy的并集,并把它添加到子集的集合中,以代替被删除後的Sx和Sy。
例如,其中S = {1, 2, 3, 4, 5, 6}。首先使用id(x),初始化結果:{1},{2},{3},{4},{5},{6}。
現在執行union(1,4)得到{1,4},執行union(4,5)得到{1,4,5},此時集合結果:{1,4,5},{2},{3},{6}。
那麼此時執行find(1)或者find(4)或者find(5)傳回子集{1,4,5},執行find(3)傳回子集{3}。
上面就是并查算法的應用思想,那麼影響并查算法的時間效率,就是id(x)和union(x)函數的具體實作來決定。
此處對于id(x)和union(x)的實作,我采用樹的性質來實作,把已經構造的邊形成一棵樹,當有新增的邊時,且新增的邊所在樹的層數或者所有節點總數小于目前構造的樹,那麼我們就把新增的邊所在樹的根節點改變成目前正在構造的樹的根節點的直接子節點。
例如合并子集{1,4,5,2}(PS:該子集構成的樹根節點為1)}和{3,6}(PS:該子集構成的樹的根節點為3),那麼可以把根節點3直接轉換為1的一個直接子節點即可。具體如下圖所示:
講完上面的定義及思想,下面就來具體看看對于2.1中示例圖實作的編碼應用。
首先,是初始化id(x),這裡我首先令每一個單節點樹的id(x)值為-1。
然後,是find(x)的實作:
最後,是union(x)的實作:
到這裡後,看一下,構造樹型id(x)值的具體圖:
首先頂點1到5的id(x) = {-1, -1, -1, -1, -1},即表示剛開始,所有頂點均為根節點。(PS:後面示例id(x)、find(x)和union(x, y)中對于數組中元素均為1開始,不是0開始計算數組中元素,這樣是方面描述,請大家不要見怪喲。注意,下面圖中id = 2表示根節點為頂點3)
(1)選擇第1條邊,2-3,5
此時id(2) = -1,find(2) = 2根節點為2。id(3) = -1,find(3) = 3根節點為3。根據union(x)函數可知,由于id(find(2)) >= id(find(3)),是以id(find(2)) = idb = 2,id(find(3)) = num = -2
此時id(x) = {-1, 2, -2, -1, -1 }
(2)選擇第2條邊,1-2,5
此時,id(1) = -1,find(1) = 1根節點為1。Id(2) = 2,find(2) = 3根節點為3。根據union(x)函數可知,由于id(find(1)) > id(find(2)),是以id(find(1)) = idb = 2,id(find(2)) = num = -3
此時id(x) = {2, 2, -3, -1, -1 }
(3)選擇第3條邊,3-5,6
此時,id(3) = -3,find(3) = 3根節點為3。Id(5) = -1,find(5) = 5根節點為5。根據union(x)函數可知,由于id(find(3)) < id(find(5)),是以id(find(5)) = ida = 2,id(find(3)) = num = -4
此時id(x) = {2, 2, -4, -1, 2}
(4)選擇第4條邊,4-5,12(此處也是最小生成樹的最後一條邊)
此時,id(4) = -1,find(4) = 4根節點為4。Id(5) = 2,find(5) = 3根節點為3。根據union(x)函數可知,由于id(find(4)) > id(find(5)),是以id(find(4)) = idb = 2,id(find(5)) = num = -5
此時id(x) = {2, 2, -5, 2, 2 }
2.3 具體編碼(最佳時間效率)
運作結果: