1 覓食行為
指魚循着食物多的方向遊動的一種行為,人工魚X i X_iXi在其視野内随機選擇一個狀态X j X_jXj,分别計算它們的目标函數值進行比較,如果發現Y j Y_jYj比Y i Y_iYi優(Y j Y_jYj和Y i Y_iYi分别為X j X_jXj和X i X_iXi的适應度值),則Xi向Xj的方向移動一步;否則,X i X_iXi繼續在其視野内選擇狀态X j X_jXj,判斷是否滿足前進條件,反複嘗試t r y n u m b e r trynumbertrynumber次後,仍沒有滿足前進條件,則随機移動一步使X i X_iXi到達一個新的狀态。表達式如下:
X j = X i + r a n d ( ) ∗ v i s u a l (1) X_j=X_i+rand()*visual \tag{1}Xj=Xi+rand()∗visual(1)
X n e x t = X i + r a n d ( ) ∗ s t e p ∗ X j − X i ∣ ∣ X j − X i ∣ ∣ (2) X_{next}=X_i+rand()step\frac{X_j-X_i}{\left | \left | X_j-X_i \right | \right |}\tag{2}Xnext=Xi+rand()∗step∗∣∣Xj−Xi∣∣Xj−Xi(2)
X n e x t = X i + r a n d ( ) ∗ s t e p (3) X_{next}=X_i+rand()*step \tag{3}Xnext=Xi+rand()∗step(3)
其中rand()是介于0和1之間的随機數。
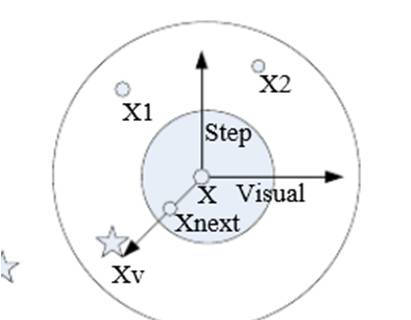
人 工 魚 的 視 覺 描 述 人工魚的視覺描述人工魚的視覺描述
架構圖如下所示:
僞代碼段如下:
2 聚群行為
魚在遊動過程中為了保證自身的生存和躲避危害會自然地聚內建群 。人工魚X i X_iXi搜尋其視野内(d i j < v i s u a l d_{ij}<visualdij<visual)的夥伴數目n f n_fnf及中心位置X c X_cXc,若Y c / n f < δ Y i Y_c/n_f< δY_iYc/nf<δYi(求極小值時使用小于号,在求極大值時則相反;Y c Y_cYc和Y i Y_iYi分别為X c X_cXc和X i X_iXi的适應度值),表明夥伴中心位置狀态較優且不太擁擠,則X i X_iXi朝夥伴的中心位置移動一步,否則執行覓食行為;
3 追尾行為
指魚向其視野區域内的最優方向移動的一種行為。人工魚X i X_iXi搜尋其視野内(d i j < v i s u a l d_{ij}<visualdij<visual)适應度最高的個體X j X_jXj,其适應度值為Y j Y_jYj,并探索人工魚X j X_jXj視野内的夥伴數目n f n_fnf,若Y j / n f < δ Y i Y_j/n_f< δY_iYj/nf<δYi,表明X j X_jXj狀态較優且不太擁擠,則X i X_iXi朝X j X_jXj位置移動一步,否則執行覓食行為;
4 算法總述
綜上所述,算法在運算過程中,會同時進行聚群和追尾行為。而覓食行為屬于這兩種行為中發現聚群對象或者追尾對象附近擁擠度過大時,人工魚選擇的行為方式,若在覓食過程中,未發現比自身适應度高的人工魚,則按步長step随機移動。最後對聚群行為和追尾行為得到的适應度值進行比較,選擇優秀的人工魚作為下一代的個體。其總架構圖如下:
2 分析擁擠度因子δ δδ
2.1 擁擠度因子的取值
在求極小值問題中:δ = α n m a x , α ∈ ( 0 , 1 ] δ=αn_{max}, α∈(0,1]δ=αnmax,α∈(0,1]
在求極大值問題中:δ = 1 α n m a x , α ∈ ( 0 , 1 ] δ=\frac{1}{αn_{max}},α∈(0,1]δ=αnmax1,α∈(0,1]
其中α αα為極值接近水準,n m a x n_{max}nmax為期望在該鄰域内聚集的最大人工魚數目。
2.2 擁擠度因子的作用機理
對追尾行為的描述
圖中af0為人工魚af1-5在各自視野内的最優人工魚,其實物濃度為Y j Y_jYj,C1為以af0為圓心,以視野範圍為半徑的圓,即能探知af0的最遠距離,人工魚越靠近af0,狀态越優。
求極大值情況下:當δ n f ≤ 1 δn_f\leq 1δnf≤1時,所有人工魚af1-5都執行追尾行為,向af0遊動;
δ = 1 α n m a x δ=\frac{1}{αn_{max}}δ=αnmax1
δ n f = n f α n m a x ≤ 1 δn_f =\frac{n_f}{αn_{max}}\leq 1δnf=αnmaxnf≤1
當α αα=1的時候,可以明顯看出來n f ≤ n m a x n_f \leq n_{max}nf≤nmax,即說明人工魚視野範圍内不擁擠。
當δ n f > 1 δn_f >1δnf>1時,若C2的食物濃度為Y j δ n f \frac{Y_j}{δn_f }δnfYj的等濃度食物圈,則C2與C1間的人工魚af1、af2、af3執行追尾行動,向af0遊動,人工魚af4、af5執行覓食行為。此時δnf 越大執行追尾行動的人工魚越少,反之越多。
2.3 擁擠度因子的影響
以極大值為例(極小值的情況正好和極大值相反), δ δδ越大,表明允許的擁擠程度越小,人工魚擺脫局部最優的能力越強;但是收斂的速度會有所減緩,這主要因為人工魚在逼近極值的同時,會因避免過分擁擠而随機走開或者受其它人工魚的排斥作用,不能精确逼近極值點。可見,δ δδ的引入避免了人工魚過度擁擠而陷入局部極值,另一方面,該參數會使得位于極值點附近的人工魚之間存在互相排斥的影響,而難以向極值點精确逼近,是以,對于某些局部極值不是很嚴重的具體問題,可以忽略擁擠的因素,進而在簡化算法的同時也加快了算法的收斂速度和提高結果的精确程度。
1 matlab版本
2014a
2 參考文獻
[1] 包子陽,餘繼周,楊杉.智能優化算法及其MATLAB執行個體(第2版)[M].電子工業出版社,2016.
[2]張岩,吳水根.MATLAB優化算法源代碼[M].清華大學出版社,2017.