1. 引言
許多應用都需要動态集合結構,它至少需要支援Insert,search和delete字典操作。散清單(hash table)是實作字典操作的一種有效的資料結構。
2. 直接尋址表
在介紹散清單之前,我們先介紹直接尋址表。
當關鍵字的全域U(關鍵字的範圍)比較小時,直接尋址是一種簡單而有效的技術。我們假設某應用要用到一個動态集合,其中每個元素的關鍵字都是取自于全域U={0,1,…,m-1},其中m不是一個很大的數。另外,假設每個元素的關鍵字都不同。
為表示動态集合,我們用一個數組,或稱為直接尋址表(direct-address table),記為T[0~m-1],其中每一個位置(slot,槽)對應全域U中的一個關鍵字,對應規則是,槽k指向集合中關鍵字為k的元素,如果集合中沒有關鍵字為k的元素,則T[k]=NIL。
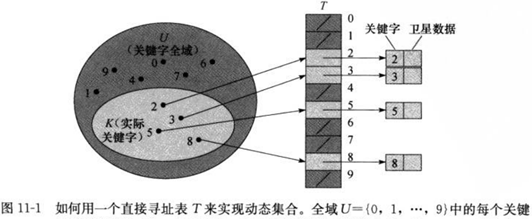
幾種字典操作實作起來非常簡單:
上述的每一個操作的時間均為O(1)時間。
在某些應用中,我們其實可以把對象作為元素直接儲存在尋址表的槽中,而不需要像上圖所示使用指針指向該對象,這樣可以節省空間。
3. 散清單
(1) 直接尋址的缺點
我們可以看出,直接尋址技術有幾個明顯的缺點:如果全域U很大,那麼表T 将要申請一段非常長的空間,很可能會申請失敗;對于全域較大,但是元素卻十分稀疏的情況,使用這種存儲方式将浪費大量的存儲空間。
(2) 散列函數
為了克服直接尋址技術的缺點,而又保持其快速字典操作的優勢,我們可以利用散列函數(hash function)
h:U→{0,1,2,…,m-1}
來計算關鍵字k所在的的位置,簡單的講,散列函數h(k)的作用是将範圍較大的關鍵字映射到一個範圍較小的集合中。這時我們可以說,一個具有關鍵字k的元素被散列到槽h(k)上,或者說h(k)是關鍵字k的散列值。
示意圖如下:
這時會産生一個問題:兩個關鍵字可能映射到同一槽中(我們稱之為沖突(collision)),并且不管你如何優化h(k)函數,這種情況都會發生(因為|U|>m)。
是以我們現在面臨兩個問題,一是遇到沖突時如何解決;二是要找出一個的函數h(k)能夠盡量的減少沖突;
(3) 通過連結清單法解決沖突
我們先來解決第一個問題。
解決辦法就是,我們把同時散列到同一槽中的元素以連結清單的形式“串聯”起來,而該槽中儲存的是指向該連結清單的指針。如下圖所示:
采用該解決辦法後,我們可以通過如下的操作方式來進行字典操作:
下面我們來分析上圖各操作的性能。
首先是插入操作,很明顯時間為O(1)。
然後分析删除操作,其花費的時間相當于從連結清單中删除一個元素的時間:如果連結清單T[h(k)]是雙連結清單,花費的時間為O(1);如果連結清單T[h(k)]是單連結清單,則花費的時間和查找操作的漸進運作時間相同。
下面我們重點分析查找運作時間:
首先,我們假定任何一個給定元素都等可能地散列在散清單T的任何一個槽位中,且與其他元素被散列在T的哪個位置無關。我們稱這個假設為簡單均勻散列(simple uniform hashing)。
不失一般性,我們設散清單T的m個槽位散列了n個元素,則平均每個槽位散列了α = n/m個元素,我們稱α為T的裝載因子(load factor)。我們記位于槽位j的連結清單為T[j](j=1,2,…,m-1),而nj表示連結清單T[j]的長度,于是有
n = n0+n1+…+nm-1,
且E[nj] = α = n / m。
現在我們分查找成功和查找不成功兩種情況讨論。
① 查找不成功
在查找不成功的情況下,我們需要周遊連結清單T[j]的每一個元素,而連結清單T[j]的長度是α,是以需要時間O(α),加上索引到T(j)的時間O(1),總時間為θ(1 + α)。
② 查找成功
在查找成功的情況下,我們無法準确知道周遊到連結清單T[j]的何處停止,是以我們隻能讨論平均情況。
我們設xi是散清單T的第i個元素(假設我們按插入順序對散清單T中的n個元素進行了1~n的編号),ki表示xi.key,其中i = 1,2,…,n,再定義随機變量Xij=I{h(ki)=h(kj)},即:
在簡單均勻散列的假設下有
P{h(ki)=h(kj)} = 1 / m,
E[Xij] = 1 / m。
則所需檢查的元素的數目的期望是:
是以,一次成功的檢查所需要的時間是O(2 + α / 2 –α / 2n) = θ(1 + α)。
綜合上面的分析,在平均下,全部的字典操作都可以在O(1)時間下完成。
4. 散列函數
現在我們來解決第二個問題:如何構造一個好的散列函數。
一個好的散列函數應(近似地)滿足簡單均勻散列:每個關鍵字都等可能的被散列到各個槽位,并與其他關鍵字散列到哪一個槽位無關(但很遺憾,我們一般無法檢驗這一條件是否成立)。
在實際應用中,常常可以可以運用啟發式方法來構造性能好的散列函數。設計過程中,可以利用關鍵字分布的有用資訊。一個好的方法導出的散列值,在某種程度上應獨立于資料可能存在的任何模式。
下面給出兩種基本的構造散列函數的方法:
(1) 除法散列法
除法散列法的做法很簡單,就是讓關鍵字k去除以一個數m,取餘數,這樣就将k映射到m個槽位中的某一個,即散列函數是:
h(k) = k mod m ,
由于隻做一次除法運算,該方法的速度是非常快的。但應當注意的是,我們在選取m的值時,應當避免一些選取一些值。例如,m不應是2的整數幂,因為如果m = 2 ^ p,則h(k)就是k的p個最低位數字。除非我們已經知道各種最低p位的排列是等可能的,否則我們最好慎重的選擇m。而一個不太接近2的整數幂的素數,往往是較好的選擇。
(2) 乘法散列法
該方法包含兩個步驟。第一步:用關鍵字k乘以A(0 < A < 1),并提取kA的小數部分;第二步:用m乘以這個值,在向下取整,即散列函數是:
h(k) = [m (kA mod 1)],
這裡“kA mod 1”的是取kA小數部分的意思,即kA –[kA]。
乘法散列法的一個優點是,一般我們對m的選擇不是特别的關鍵,一般選擇它為2的整數幂即可。雖然這個方法對任意的A都适用,但Knuth認為,A ≈ (√5 - 1)/ 2 = 0.618033988…是一個比較理想的值
(5) 布隆過濾器
布隆過濾器(Bloom Filter)是一種常被用來檢驗一個元素是否在一個集合裡面的算法(從這裡我們可以看出,這個集合隻需要儲存比對元素的“指紋”即可,而不需要儲存比對元素的全部資訊),由一個很長的二進制向量和一系列随機映射函數組成。相較于其他算法,它具有空間使用率高,檢測速度快等優點。
在介紹布隆過濾器之前,我們先假設這樣一種場景:某公司緻力于解決使用者常常遭遇騷擾電話的問題。該公司打算建立一個騷擾電話号碼的黑名單,即把所有騷擾電話的号碼儲存到一張hash表中。當使用者接到某個陌生電話時,伺服器會立即将該号碼與黑名單進行比對,若比對成功,則對該号碼進行攔截。
他們當然不會直接将騷擾電話号碼儲存在hash表中,而是對每一個号碼利用某種算法進行資料壓縮,最終得到一個8位元組的資訊指紋,然後将其存入表中。但即便如此,問題還是來了:由于hash表的空間使用率大約隻有50%,等價換算過來,儲存一個号碼将要花費16位元組的空間。按照這樣計算,儲存1億個号碼将要花費大約1.6G的空間,儲存幾十億的号碼可能需要上百G的空間。那麼有沒有更好解決辦法呢?
這時,布隆過濾器就派上用場了。假設我們有1億條騷擾電話号碼需要記錄,我們的做法是,首先建立一個2億位元組(即16億位,并假設我們對這16億位以1~16億的順序進行了編号)的向量,将每位都置為0。當要插入某個電話号碼x時,我們使用某種算法(該算法可以做到每個位被映射的機率是一樣的,且某個映射的分布與其他的映射分布無關)讓号碼x映射到1~16億中的8個位上,然後把這8個位設為1。當查找時,利用同樣的方法将号碼映射到8個位上,若這8個位都為1,則說明該号碼在黑名單中,否則就不在。
我們可以發現,布隆過濾器的做法在思想上和hash函數将關鍵字映射到hash表的做法很相似,是以布隆過濾器也會遇到沖突問題,這會導緻将一個“好”的号碼誤判為騷擾号碼(但絕對不會将騷擾号碼誤判為一個“好”的号碼)。下面我們通過計算來證明,在大多數情況和場景中,這種誤判我們是可以忍受的。
假設某布隆過濾器共有的m個槽位,我們要把n個号碼添加到其中,而每個号碼會映射k個槽位。那麼,添加這n個号碼将會産生kn次映射。因為這m個槽位中,每個槽被映射到的機率是相等的。是以,
在一次映射中,某個槽位被映射到的機率(即該槽位值為1的機率)為
該槽位值為0的機率為
經過kn次映射後,某個槽值為0的機率為
為1的機率為
是以,誤判(k個槽位均為1)的機率就為
利用
,上式可化為:
這時我們注意到,當k=1時,情況就就變成了hash table的情況,
根據自變量的不同我們分以下兩種方式讨論:
① 我們把誤判率p看作關于裝載因子α的函數(k看作常數),這時我們從函數
的函數圖像
中可以得出一下結論:
随着裝載因子α(α = n / m)的增大,誤判率(或者是産生沖突的機率)也将增大,但增長速度逐漸減慢。
要使誤判率小于0.5,裝載因子必須小于0.7。這也從某種程度上解釋了為什麼JDK HashMap的裝載因子預設是0.75。
② 我們把誤判率p看作關于k的函數(α作為常數),通過對p求導分析,我們發現,當k=ln2 / α時,誤判率p取得最小值。此時,p = 2^(-k)(或者k = – ln p / ln 2),這個結論讓我們能夠根據可以忍受的誤判率計算出最為合适的k值。
下面給出一個BloomFilter的Java實作代碼(來自:https://github.com/MagnusS/Java-BloomFilter,隻是把其中的變量和方法名換成了上文提及的):