(小技巧記錄:部落格園編輯的網頁界面變小了使用Ctrl ++來變大網頁字型)
通過雷達,雷射掃描,立體錄影機等三維測量裝置擷取的點雲資料,具有資料量大,分布不均勻等特點,作為三維領域中一個重要的資料來源,點雲主要是表征目标表面的海量點的集合,并不具備傳統網格資料的幾何拓撲資訊,是以點雲資料進行中最為核心的問題就是建立離散點間的拓撲關系,實作基于鄰域關系的快速查找。
k-d樹 (k-dimensional樹的簡稱),是一種分割k維資料空間的資料結構。主要應用于多元空間關鍵資料的搜尋(如:範圍搜尋和最近鄰搜尋)。K-D樹是二進制空間分割樹的特殊的情況。用來組織表示K維空間中點的幾何,是一種帶有其他限制的二分查找樹,為了達到目的,通常隻在三個次元中進行處理是以所有的kd_tree都将是三維的kd_tree,kd_tree的每一維在指定次元上分開所有的位元組點,在樹 的根部所有子節點是以第一個指定的次元上被分開。
k-d樹算法可以分為兩大部分,一部分是有關k-d樹本身這種資料結建構立的算法,另一部分是在建立的k-d樹上如何進行最鄰近查找的算法。
建構算法
k-d樹是一個二叉樹,每個節點表示一個空間範圍。表1給出的是k-d樹每個節點中主要包含的資料結構。
域名
資料類型
描述
Node-data
資料矢量
資料集中某個資料點,是n維矢量(這裡也就是k維)
Range
空間矢量
該節點所代表的空間範圍
split
整數
垂直于分割超平面的方向軸序号
Left
k-d樹
由位于該節點分割超平面左子空間内所有資料點所構成的k-d樹
Right
由位于該節點分割超平面右子空間内所有資料點所構成的k-d樹
parent
父節點
先以一個簡單直覺的執行個體來介紹k-d樹算法。假設有6個二維資料點{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},資料點 位于二維空間内(如圖1中黑點所示)。k-d樹算法就是要确定圖1中這些分割空間的分割線(多元空間即為分割平面,一般為超平面)。下面就要通過一步步展 示k-d樹是如何确定這些分割線的。
由于此例簡單,資料次元隻有2維,是以可以簡單地給x,y兩個方向軸編号為0,1,也即split={0,1}。
(1)确定split域的首先該取的值。分别計算x,y方向上資料的方差得知x方向上的方差最大,是以split域值首先取0,也就是x軸方向;
(2)确定Node-data的域值。根據x軸方向的值2,5,9,4,8,7排序選出中值為7,是以Node-data = (7,2)。這樣,該節點的分割超平面就是通過(7,2)并垂直于split = 0(x軸)的直線x = 7;
(3)确定左子空間和右子空間。分割超平面x = 7将整個空間分為兩部分,如圖2所示。x < = 7的部分為左子空間,包含3個節點{(2,3),(5,4),(4,7)};另一部分為右子空間,包含2個節點{(9,6),(8,1)}。
(4)k-d樹的建構是一個遞歸的過程。然後對左子空間和右子空間内的資料重複根節點的過程就可以得到下一級子節點(5,4)和(9,6)(也就是 左右子空間的'根'節點),同時将空間和資料集進一步細分。如此反複直到空間中隻包含一個資料點,如圖1所示。最後生成的k-d樹如圖3所示。
關于Kdtree算法的相關内容網上有很多比如blog.csdn.net/silangquan/article/details/41483689
查找算法
在k-d樹中進行資料的查找也是特征比對的重要環節,其目的是檢索在k-d樹中與查詢點距離最近的資料點。這裡先以一個簡單的執行個體來描述最鄰近查找的基本思路。
星号表示要查詢的點(2.1,3.1)。通過二叉搜尋,順着搜尋路徑很快 就能找到最鄰近的近似點,也就是葉子節點(2,3)。而找到的葉子節點并不一定就是最鄰近的,最鄰近肯定距離查詢點更近,應該位于以查詢點為圓心且通過葉 子節點的圓域内。為了找到真正的最近鄰,還需要進行'回溯'操作:算法沿搜尋路徑反向查找是否有距離查詢點更近的資料點。此例中先從(7,2)點開始進行 二叉查找,然後到達(5,4),最後到達(2,3),此時搜尋路徑中的節點為<(7,2),(5,4),(2,3)>,首先以(2,3)作為 目前最近鄰點,計算其到查詢點(2.1,3.1)的距離為0.1414,然後回溯到其父節點(5,4),并判斷在該父節點的其他子節點空間中是否有距離查 詢點更近的資料點。以(2.1,3.1)為圓心,以0.1414為半徑畫圓,如圖4所示。發現該圓并不和超平面y = 4交割,是以不用進入(5,4)節點右子空間中去搜尋。
PCL中kd_tree子產品及類的介紹
對此類的函數有更加詳細的介紹
類KdTree關鍵成員函數
(
cloud,
)
設定輸入點雲,參數cloud 作為輸入點雲的共享指針引用,indices為在kd_tree中使用的點對應的索引,如果不設定,則預設使用整個點雲填充kd_tree
int
index,
k,
std::vector< int > &
k_indices,
std::vector< float > &
k_sqr_distances
const
純虛函數,具體實作在其子類KdTreeFLANN中,其用來進行K 領域搜尋,k_sqr_distances 為搜尋完成後每個鄰域點與查詢點的歐式距離,
還更多的成員的介紹檢視 docs.pointclouds.org/trunk/classpcl_1_1_kd_tree.html#ac81c442ff9c9b1e03c10cb55128e726d
應用執行個體
建立檔案
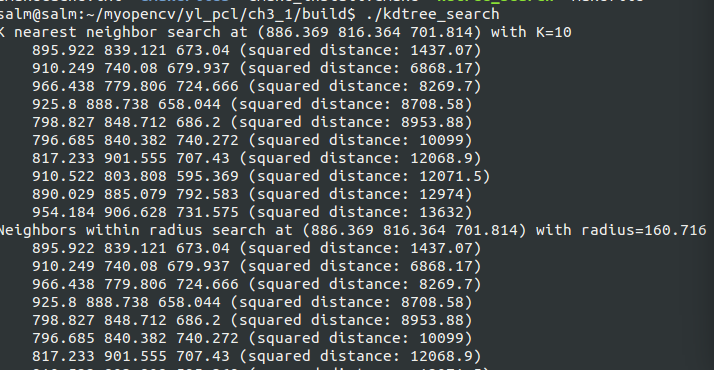
編譯執行的結果如圖:
微信公衆号号可掃描二維碼一起共同學習交流
未完待續************************************8