圖像處理之三角法圖像二值化圖像處理之三角法圖像二值化

三角法求門檻值最早見于Zack的論文《Automatic measurement of sister chromatid exchange frequency》主要是用于染色體的研究，該方法是使用直方圖資料，基于純幾何方法來尋找最佳門檻值，它的成立條件是假設直方圖最大波峰在靠近最亮的一側，然後通過三角形求得最大直線距離，根據最大直線距離對應的直方圖灰階等級即為分割門檻值，圖示如下：

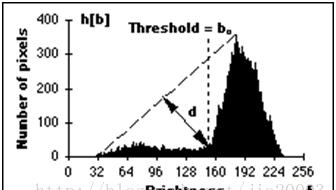
對上圖的詳細解釋：

在直方圖上從最高峰處bmx到最暗對應直方圖bmin(p=0)%構造一條直線，從bmin處開始計算每個對應的直方圖b到直線的垂直距離，知道bmax為止，其中最大距離對應的直方圖位置即為圖像二值化對應的門檻值T。

擴充情況：

有時候最大波峰對應位置不在直方圖最亮一側，而在暗的一側，這樣就需要翻轉直方圖，翻轉之後求得值，用255減去即得到為門檻值T。擴充情況的直方圖表示如下：

二：算法步驟

1. 圖像轉灰階

2. 計算圖像灰階直方圖

3. 尋找直方圖中兩側邊界

4. 尋找直方圖最大值

5. 檢測是否最大波峰在亮的一側，否則翻轉

6. 計算門檻值得到門檻值T，如果翻轉則255-T

三：代碼實作

四：運作結果

2016年最後一篇，這裡祝大家元旦快樂，歡迎在2017繼續關注本部落格，分享有用實用的圖像處理知識本人會一直堅持到永遠！

<a href="http://edu.51cto.com/course/course_id-6335.html">學習圖像處理基礎入門課程 - 點選這裡</a>