1 引言
模拟退火算法(Simulated Annealing,SA)的思想最早由Metropolis等人于1953年提出:Kirkpatrick于1983年第一次使用模拟退火算法求解組合最優化問題[1] 。模拟退火算法是一種基于MonteCarlo疊代求解政策的随機尋優算法, 其出發點是基于實體中固體物質的退火過程與一般組合優化問題之間的相似性。其目的在于為具有NP(Non-deterministic Polynomial) 複雜性的問題提供有效的近似求解算法,它克服了其他優化過程容易陷入局部極小的缺陷和對初值的依賴性。
模拟退火算法是一種通用的優化算法,是局部搜尋算法的擴充。它不同于局部搜尋算法之處是以一定的機率選擇鄰域中目标值大的劣質解。從理論上說,它是一種全局最優算法。模拟退火算法以優化問
題的求解與實體系統退火過程的相似性為基礎, 它利用Metropolis算法并适當地控制溫度的下降過程來實作模拟退火,進而達到求解全局優化問題的目的[2].
模拟退火算法是一種能應用到求最小值問題的優化過程。在此過程中,每一步更新過程的長度都與相應的參數成正比,這些參數扮演着溫度的角色。與金屬退火原理相類似,在開始階段為了更快地最小
化,溫度被升得很高,然後才慢慢降溫以求穩定。
目前,模拟退火算法迎來了興盛時期,無論是理論研究還是應用研究都成了十分熱門的課題[3-7]。尤其是它的應用研究顯得格外活躍,已在工程中得到了廣泛應用,諸如生産排程、控制工程、機器學習、神經網絡、模式識别、圖像處理、離散/連續變量的結構優化問題等領域。它能有效地求解正常優化方法難以解決的組合優化問題和複雜函數優化問題,适用範圍極廣。
模拟退火算法具有十分強大的全局搜尋性能,這是因為比起普通的優化搜方法,它采用了許多獨特的方法和技術:在模拟退火算法中,基本不用搜尋空間的知識或者其他的輔助資訊,而隻是定義鄰域
結構,在其鄰域結構内選取相鄰解,再利用目标函數進行評估:模拟退火算法不是采用确定性規則,而是采用機率的變遷來指導它的搜尋方向,它所采用的機率僅僅是作為一種工具來引導其搜尋過程朝着更優化解的區域移動。是以,雖然看起來它是一種盲目的搜尋方法,但實際上有着明确的搜尋方向。
2 模拟退火算法理論
模拟退火算法以優化問題求解過程與實體退火過程之間的相似性為基礎,優化的目标函數相當于金屬的内能,優化問題的自變量組合狀态空間相當于金屬的内能狀态空間,問題的求解過程就是找一個組
合狀态, 使目标函數值最小。利用Me to polis算法并适當地控制溫度的下降過程實作模拟退火,進而達到求解全局優化問題的目的[8].
2.1實體退火過程
模拟退火算法的核心思想與熱力學的原理極為類似。在高溫下,液體的大量分子彼此之間進行着相對自由移動。如果該液體慢慢地冷卻,熱能原子可動性就會消失。大量原子常常能夠自行排列成行,形成一個純淨的晶體,該晶體在各個方向上都被完全有序地排列在幾百萬倍于單個原子的距離之内。對于這個系統來說,晶體狀态是能量最低狀态,而所有緩慢冷卻的系統都可以自然達到這個最低能量狀态。實際上,如果液态金屬被迅速冷卻,則它不會達到這一狀态,而隻能達到一種隻有較高能量的多晶體狀态或非結晶狀态。是以,這一過程的本質在于緩慢地冷卻,以争取足夠的時間,讓大量原子在喪失可動性之前進行重新分布,這是確定能量達到低能量狀态所必需的條件。簡單而言,實體退火過程由以下幾部分組成:加溫過程、等溫過程和冷卻過程。
加溫過程
其目的是增強粒子的熱運動,使其偏離平衡位置。當溫度足夠高時,固體将熔解為液體,進而消除系統原先可能存在的非均勻态,使随後進行的冷卻過程以某一平衡态為起點。熔解過程與系統的能量增
大過程相聯系,系統能量也随溫度的升高而增大。
等溫過程
通過實體學的知識得知,對于與周圍環境交換熱量而溫度不變的封閉系統,系統狀态的自發變化總是朝着自由能減小的方向進行:當自由能達到最小時,系統達到平衡态。
冷卻過程
其目的是使粒子的熱運動減弱并逐漸趨于有序,系統能量逐漸下降,進而得到低能量的晶體結構。
2.2 模拟退火原理
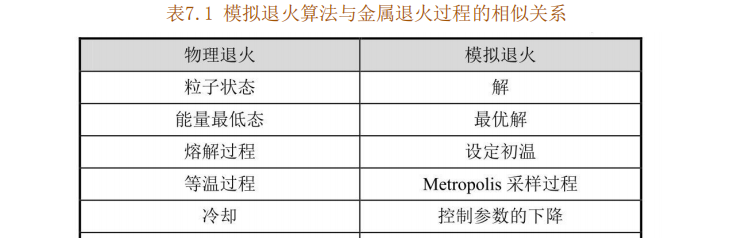
模拟退火算法來源于固體退火原理,将固體加溫至充分高,再讓其徐徐冷卻。加溫時,固體内部粒子随溫升變為無序狀,内能增大:而徐徐冷卻時粒子漸趨有序,在每個溫度上都達到平衡态,最後在常
溫時達到基态,内能減為最小。模拟退火算法與金屬退火過程的相似關系如表7.1所示。根Metropolis準則, 粒子在溫度7時趨于平衡的機率為exp(-▲E/T) , 其中E為溫度7時的内能, ▲E為其改變量。用
固體退火模拟組合優化問題,将内能E模拟為目标函數值,溫度7演化成控制參數,即得到解組合優化問題的模拟退火算法:由初始解%和控制參數初值7開始,對目前解重複“産生新解→計算目标函數差一接受或舍棄”的疊代,并逐漸減小T值,算法終止時的目前解即為所得近似最優解, 這是基MonteCarlo疊代求解法的一種啟發式随機搜尋過程。退火過程由冷卻進度表控制,包括控制參數的初值7及其衰
減因子K、每個7值時的疊代次數I和停止條件。
2.3 模拟退火算法思想
模拟退火的主要思想是:在搜尋區間随機遊走(即随機選擇點),再利用Metropolis抽樣準則, 使随機遊走逐漸收斂于局部最優解。而溫度是Metropolis算法中的一個重要控制參數,可以認為這個參數的大小控制了随機過程向局部或全局最優解移動的快慢。Metropolis是一種有效的重點抽樣法, 其算法為:系統從一個能量狀态變化到另一個狀态時,相應的能量從E變化到E,其機率為
這樣經過一定次數的疊代,系統會逐漸趨于一個穩定的分布狀态。
重點抽樣時,新狀态下如果向下,則接受(局部最優);若向上(全局搜尋),則以一定機率接受。模拟退火算法從某個初始解出發,經過大量解的變換後,可以求得給定控制參數值時組合優化問題的相對最優解。然後減小控制參數7的值, 重複執行Metropolis算法,就可以在控制參數T趨于零時,最終求得組合優化問題的整體最優解。控制參數的值必須緩慢衰減。溫度是Metropolis算法的一個重要控制參數, 模拟退火可視為遞減控制參數7時Metro pl is算法的疊代。開始時7值大, 可以接受較差的惡化解;随着7的減小,隻能接受較好的惡化解;最後在7趨于0時,就不再接受任何惡化解了。
在無限高溫時,系統立即均勻分布,接受所有提出的變換。T的衰減越小, 7到達終點的時間越長; 但可使馬爾可夫(Markov) 鍊減小,以使到達準平衡分布的時間變短。
2.4 模拟退火算法的特點
模拟退火算法适用範圍廣,求得全局最優解的可靠性高,算法簡單,便于實作;該算法的搜尋政策有利于避免搜尋過程因陷入局部最優解的缺陷,有利于提高求得全局最優解的可靠性。模拟退火算法具
有十分強的魯棒性,這是因為比起普通的優化搜尋方法,它采用許多獨特的方法和技術。主要有以下幾個方面:
(1)以一定的機率接受惡化解。
模拟退火算法在搜尋政策上不僅引入了适當的随機因素,而且還引入了實體系統退火過程的自然機理。這種自然機理的引入,使模拟退火算法在疊代過程中不僅接受使目标函數值變“好”的點,而且還能夠以一定的機率接受使目标函數值變“差”的點。疊代過程中出現的狀态是随機産生的,并且不強求後一狀态一定優于前一狀态,接受機率随着溫度的下降而逐漸減小。很多傳統的優化算法往往是确定性
的,從一個搜尋點到另一個搜尋點的轉移有确定的轉移方法和轉移關系,這種确定性往往可能使得搜尋點遠達不到最優點,因而限制了算法的應用範圍。而模拟退火算法以一種機率的方式來進行搜尋,增加了搜尋過程的靈活性。
(2)引進算法控制參數。
引進類似于退火溫度的算法控制參數,它将優化過程分成若幹階段, 并決定各個階段下随機狀态的取舍标準, 接受函數由Metropolis算法給出一個簡單的數學模型。模拟退火算法有兩個重要的步驟:一
是在每個控制參數下,由前疊代點出發,産生鄰近的随機狀态,由控制參數确定的接受準則決定此新狀态的取舍,并由此形成一定長度的随機Markov鍊; 二是緩慢降低控制參數, 提高接受準則, 直至控制參數趨于零,狀态鍊穩定于優化問題的最優狀态,進而提高模拟退火算法全局最優解的可靠性。
(3)對目标函數要求少。
傳統搜尋算法不僅需要利用目标函數值,而且往往需要目标函數的導數值等其他一些輔助資訊才能确定搜尋方向:當這些資訊不存在時,算法就失效了。而模拟退火算法不需要其他的輔助資訊,而隻是
定義鄰域結構,在其鄰域結構内選取相鄰解,再用目标函數進行評估。
2.5模拟退火算法的改進方向
在確定一定要求的優化品質基礎上,提高模拟退火算法的搜尋效率,是對模拟退火算法改進的主要内容[9-10]。有如下可行的方案:選擇合适的初始狀态;設計合适的狀态産生函數,使其根據搜尋程序的
需要表現出狀态的全空間分散性或局部區域性:設計高效的退火過程;改進對溫度的控制方式:采用并行搜尋結構;設計合适的算法終止準則:等等。
此外,對模拟退火算法的改進,也可通過增加某些環節來實作。
主要的改進方式有:
(1)增加記憶功能。為避免搜尋過程中由于執行機率接受環節而遺失目前遇到的最優解,可通過增加存儲環節,将到目前為止的最好狀态存儲下來。
(2)增加升溫或重升溫過程。在算法程序的适當時機,将溫度适當提高,進而可激活各狀态的接受機率,以調整搜尋程序中的目前狀态,避兔算法在局部極小解處停滞不前。
(3)對每一目前狀态,采用多次搜尋政策,以機率接受區域内的最優狀态,而不是标準模拟退火算法的單次比較方式。
(4)與其他搜尋機制的算法(如遺傳算法、免疫算法等)相結合。可以綜合其他算法的優點,提高運作效率和求解品質。
3 模拟退火算法流程
模拟退火算法新解的産生和接受可分為如下三個步驟:
(1)由一個産生函數從目前解産生一個位于解空間的新解;為便于後續的計算和接受,減少算法耗時,通常選擇由目前解經過簡單變換即可産生新解的方法。注意,産生新解的變換方法決定了目前新解
的鄰域結構,因而對冷卻進度表的選取有一定的影響。
(2)判斷新解是否被接受,判斷的依據是一個接受準則,最常用的接受準則是Metropolis準則:若AK 0, 則接受X作為新的目前解否則, 以機率exp(-▲E/7) 接受X”作為新的目前解X.
(3)當新解被确定接受時,用新解代替目前解,這隻需将目前解中對應于産生新解時的變換部分予以實作,同時修正目标函數值即可。此時,目前解實作了一次疊代,可在此基礎上開始下一輪試驗。若當新解被判定為舍棄,則在原目前解的基礎上繼續下一輪試驗。模拟退火算法求得的解與初始解狀态(算法疊代的起點)無關,具有漸近收斂性,已在理論上被證明是一種以機率1收斂于全局最優解的優化算法。模拟退火算法可以分解為解空間、目标函數和初始解三部分。該算法具體流程如下[8]:
(1)初始化:設定初始溫度7(充分大)、初始解狀态%(是算
法疊代的起點)、每個7值的疊代次數L:
(2)對k=1,…,L做第(3)至第(6)步;
(3)産生新解X;
(4) 計算增量A BE(X) -E(X) , 其中E() ) 為評價函數:
(5)若AK0,則接受X作為新的目前解,否則以機率
exp(-▲E/7) 接受X作為新的目前解;
(6)如果滿足終止條件,則輸出目前解作為最優解,結束程式:
(7)7逐漸減小,且T→0,然後轉第(2)步。
模拟退火算法流程如圖7.1所示。
4 關鍵參數說明
模拟退火算法的性能品質高,它比較通用,而且容易實作。不過,為了得到最優解,該算法通常要求較高的初溫以及足夠多次的抽樣,這使算法的優化時間往往過長。從算法結構知,新的狀态産生函
數、初溫、退溫函數、Markov鍊長度和算法停止準則, 是直接影響算法優化結果的主要環節。
狀态産生函數
設計狀态産生函數應該考慮到盡可能地保證所産生的候選解遍布全部解空間。一般情況下狀态産生函數由兩部分組成,即産生候選解的方式和産生候選解的機率分布。候選解的産生方式由問題的性質決
定,通常在目前狀态的鄰域結構内以一定機率産生。
初溫
溫度7在算法中具有決定性的作用,它直接控制着退火的走向。由随機移動的接受準則可知:初溫越大,獲得高品質解的幾率就越大,且Metropolis的接收率約為1。然而, 初溫過高會使計算時間增加。
為此,可以均勻抽樣一組狀态,以各狀态目标值的方差為初溫。
退溫函數
退溫函數即溫度更新函數,用于在外循環中修改溫度值。目前,最常用的溫度更新函數為指數退溫函數, 即T(n+1) =KXT(n) , 其中0<K1是一個非常接近于1的常數。
Markov鍊長度L的選取
Markov鍊長度是在等溫條件下進行疊代優化的次數, 其選取原則是在衰減參數7的衰減函數己標明的前提下,L應選得在控制參數的每一取值上都能恢複準平衡,一般L取100~1000.
算法停止準則
算法停止準則用于決定算法何時結束。可以簡單地設定溫度終值T,當F=T,時算法終止。然而,模拟火算法的收斂性理論中要求T趨向于零,這其實是不實際的。常用的停止準則包:設定終止溫度的阈
值,設定疊代次數門檻值,或者當搜尋到的最優值連續保持不變時停止搜尋。
1 matlab版本
2014a
2 參考文獻
[1] 包子陽,餘繼周,楊杉.智能優化算法及其MATLAB執行個體(第2版)[M].電子工業出版社,2016.
[2]張岩,吳水根.MATLAB優化算法源代碼[M].清華大學出版社,2017.