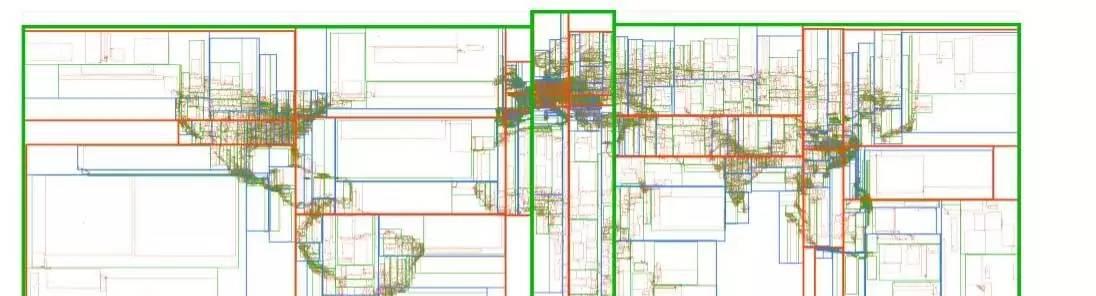
上圖為全球138,000個熱門地點的R-tree的可視化圖示
我這個人沉迷于軟體性能的提升,我在Mapbox(https://www.mapbox.com/)的職責之一就是找到能使我們的映射平台更加快速的方法。當面對大規模的空間資料時,一個最有效也是最重要的方法就是空間索引(https://en.wikipedia.org/wiki/Spatial_database#Spatial_index)。
空間索引是一系列可以通過排列幾何資料來進行高效索引的算法。例如,查詢“本區域所有的建築”、“距此點最近的1000個加油站”等問題,查詢結果往往能夠在幾毫秒内傳回,即使所要查詢的目标有幾百萬個。
空間索引是資料庫如PostGIS的基礎,同時也是我們平台的核心。在很多其他任務尤其是性能至關重要的任務中,空間索引也非常重要。特别的,在處理遙測資料時,我們需要對數百萬個GPS樣本與道路網進行比對,以産生導航所用的實時交通資料。在用戶端,我們則需要實時在地圖中展示地标,以及在滑鼠滞留時查找滑鼠所指的目标。
在過去的四年裡,我建立了一些快速的用于空間搜尋的Java 庫,包括:
rbush(https://github.com/mourner/rbush),
rbush-knn(https://github.com/mourner/rbush-knn/),
kdbush(https://github.com/mourner/kdbush),
geokdbush(https://github.com/mourner/geokdbush)。
本文中,我會努力将這幾個庫背後的原理講解清楚。
空間搜尋問題
空間資料有兩種基本查詢類型:最相鄰查詢和範圍查詢。這兩種查詢都是很多幾何問題和GIS問題的基本子產品。
K相鄰
如果給出幾千個資料點,如城市的坐标,我們如何檢索出與某特定查詢點最相鄰的點呢?
我們很自然想到的方法可能是這樣:
計算每個點與查詢點之間的距離。
按距離大小對所有的點進行排序。
傳回前k個點。
當有幾百個資料點時我們可以用這種方法,但是當我們面臨數百萬的資料點時,這種方法就顯得太慢且無法應用到實際情景。
範圍查詢和半徑查詢
如何在一個給定的範圍内檢索出所有的資料點呢?這裡又分為兩種情況,一種是所給範圍是矩形的情況(範圍查詢),另一種是所給範圍是圓的情況(半徑查詢)。
一種樸素的方法是周遊所有資料點并判斷每一個點是否在給定範圍内,但當資料集很大時,這種方法也因低效而失去了實用性。
空間樹是如何工作的
大規模地解決這兩種問題時就需要将資料點轉換到空間索引中。由于資料轉變的頻率會遠遠少于查詢的頻率,是以将資料轉變到空間索引的花銷對于之後的快速搜尋是非常值得的。
幾乎所有的空間資料結構都具有相同的原理,以實作有效的搜尋:分支和綁定(https://en.wikipedia.org/wiki/Branch_and_bound)。資料被排列在一個樹狀結構中,是以當在某一節點的某一分支不符合查詢條件時,該分支之下的所有的節點都可被略過。
R-tree
現在讓我們來看一個例子,下圖的示例将所有的輸入點分在9個矩形框中,并且每個矩形框中的點的數目相同:
現在,我們将每個矩形框再分為9個更小的矩形框:
我們會将這個過程重複幾次,找到最後每個矩形框包含的點不超過9個:
最終我們得到了R-tree(https://en.wikipedia.org/wiki/R-tree),這可以說是最常見的空間資料結構,被廣泛用于現代空間資料集和遊戲引擎,我的rbush JS庫中也實作了R-tree。
除了點之外,R-tree也可以包含矩形,用于表示任何幾何對象。同時,R-tree也可擴充到3維或高維的情況。為了易于說明,本文中以二維的情況舉例講解。
K-d tree
K-d tree (https://en.wikipedia.org/wiki/K-d_tree)是另外一種流行的空間資料結構。我的kdbush JS庫(https://github.com/mourner/kdbush),用于靜态的二維的索引,就是基于K-d tree實作的。K-d tree與R-tree類似,但與在每一層次上将資料點均分到幾個矩形框中不同的是,K-d tree會将資料點從中間分為兩部分——或左或右,或上或下,每個層次上都會在x坐标和y坐标進行劃分,如下圖所示:
與R-tree相比,K-d tree隻能包含資料點而不能包含矩形,并且不能添加或删除點。但是K-d tree在高效的同時更易實作。R-tree和K-d tree 都采用了相同的原則,即将資料組織為樹的結構。是以,下文所讨論的搜尋算法與樹的搜尋算法相同。
在樹中的範圍查詢
下圖是一個典型的空間樹:
每一個節點的孩子數都固定,本文中R-tree的例子中為9。那麼樹的深度是多少呢?對于有1,000,000 個節點的樹,高度為(log(1000000) / log(9)) = 7。
當我們在樹中執行範圍搜尋算法時,我們可以從樹根開始向下,忽略所有不滿足查詢框的矩形框。對于一個小的查詢框,這意味着在樹的每一層上隻需要搜尋幾個矩形框即可。是以,得到最終查詢結果的時間不會多于60次矩形框的比較(7 * 9 = 63),而不是1,000,000次比較,這使其比原始的循環搜尋快了16000倍。
使用R-tree 的範圍搜尋所用的平均時間為O(K log(N))(這裡K是結果的數目),而線性搜尋所用時間為O(N)。是以,R-tree的搜尋是非常高效的算法。
這裡我們選用9作為每一節點的孩子數,9是一個很不錯的預設值,但是理論上,越高的數值意味着更快的索引和更慢的查詢,反之亦然。
K相鄰查詢
相鄰查詢相較于範圍查詢稍難一些。對于一個特定的查詢點,我們怎麼知道哪棵子樹上的節點與該節點最相鄰呢?我們可以做半徑查詢,但我們不知道如何選擇半徑的大小——最相鄰的點可能在樹中離查詢點很遠的位置。如果靠增加半徑來找到一些點又會極大地降低搜尋效率。
為了在空間樹中找到一些最相鄰點,我們會利用另一個簡潔的資料結構——優先隊列(https://en.wikipedia.org/wiki/Priority_queue)。優先隊列會維護一個有序清單,該清單可以将“最小的”元素以很快的速度提取出來。為了更好地了解知識,我通常喜歡從頭開始寫一個資料結構,是以我寫的優先隊列的JS庫 tinyqueue(https://github.com/mourner/tinyqueue)可能是有史以來最好的優先隊列哦。
讓我們回顧一下R-tree的例子:
我們可以很直覺地想到,與查詢點更臨近的矩形框可能有我們想要搜尋的點。為了有效地利用這一點,我們将按從最近到最遠的順序将最大的矩形框排在隊列中,從頂層開始進行搜尋:
之後,我們“打開”相鄰的矩形框,從隊列中移除,并将它的孩子(較小的矩形框)放到隊列中與其相鄰的位置上。
重複上述步驟,當從隊列中移除的相鄰項是真正的點而不是矩形框時,這就是我們要查找的點了,隊列頂部第二個點就是第二個最相鄰的點,以此類推。
由于我們還未“打開”的矩形框中包含的點比目前矩形框中的點的距離更遠,是以我們從隊列中取出的任何點都會比剩餘的矩形框中的點的距離更近。
如果我們的空間樹很平衡的話,即所有節點的分支數基本相同,那麼我們隻需處理幾個矩形框即可,而忽略其餘的矩形框。這種政策使得該算法在搜尋過程中非常快速。
在rbush庫中,該算法在rbush-knn子產品中實作。對于地理資訊中的點,我最近釋出了另外一個kNN庫——geokdbush(https://github.com/mourner/geokdbush)。Geokdbush可以很好地處理地球的曲率和時間線的包裝。我真應該專門以geokdbush寫一篇文章,因為它是我第一次将微積分應用到實際工作中的項目。
自定義的kNN距離衡量
這種“打開”矩形框的方法是非常靈活的,除了點對點距離之外還适用于其他的距離類型。該算法依賴于查詢一個已定義的與矩形框内所有對象之間的距離的下限。如果我們自定義這個下限标準,我們依然可以使用相同的算法。這就意味着,我們可以改變算法使其搜尋最接近一條線段的K個點(而不是與一個點最相近的點):
在算法中我們唯一需要改變的就是将點與點之間的距離和點與矩形框之間的距離計算換成線段與點之間的距離和線段與矩形框之間的距離計算。
當我建立Concaveman(https://github.com/mapbox/concaveman)庫時——一個JS中快速的2D凹面庫,這樣做就顯得很友善。 它需要很多點,并生成一個如下所示的圖:
該算法以凸包(https://github.com/mikolalysenko/monotone-convex-hull-2d)開始,然後通過将它們連接配接到最接近的點的之一來向内彎曲它的每一段:
深入閱讀:A New Concave Hull Algorithm and Concaveness Measure for n-dimensional Datasets, 2012(http://www.iis.sinica.edu.tw/page/jise/2012/201205_10.pdf)
下面是一段引自論文的話:
在我們提出的凹面算法中,從邊界邊緣開始找到最近的内部點是一個耗時的過程,這些點是進一步挖掘目标點的候選點。開發更有效的方法是我們未來的研究課題。
我将資料點進行索引并執行“最近點到一個段”的查詢,這使得該算法變得更快。
未來工作
在未來在這一些列的文章中,我會将kNN算法拓展到地理資訊對象,并詳細地講解三個打包算法,即如何将資料點最好地排列到矩形框中。
最後感謝您耐心的閱讀,如果您有任何意見或問題歡迎留言。歡迎試用我們的SDKs(https://www.mapbox.com/products/),如果您能夠解決硬工程的挑戰和地圖的問題,歡迎檢視我們的job openings(https://www.mapbox.com/jobs/)。
沒有整理與歸納的知識,一文不值!高度概括與梳理的知識,才是自己真正的知識與技能。 永遠不要讓自己的自由、好奇、充滿創造力的想法被現實的架構所束縛,讓創造力自由成長吧! 多花時間,關心他(她)人,正如别人所關心你的。理想的騰飛與實作,沒有别人的支援與幫助,是萬萬不能的。
本文轉自wenglabs部落格園部落格,原文連結:http://www.cnblogs.com/arxive/p/8138586.html,如需轉載請自行聯系原作者