卡爾曼濾波模型假設k時刻的真實狀态是從(k − 1)時刻的狀态演化而來,符合下式:
(1)
Fk 是作用在 Xk−1 上的狀态變換模型(/矩陣/矢量)。
Bk 是作用在控制器向量uk上的輸入-控制模型。
Wk 是過程噪聲,并假定其符合均值為零,協方差矩陣為Qk的多元正态分布。
(2)
時刻k,對真實狀态 xk的一個測量zk滿足下式:
(3)
其中Hk是觀測模型,它把真實狀态空間映射成觀測空間,vk 是觀測噪聲,其均值為零,協方差矩陣為Rk,且服從正态分布。
(4)
初始狀态以及每一時刻的噪聲{x0, w1, ..., wk, v1 ... vk} 都認為是互相獨立的.
卡爾曼濾波要做的是:
已知:
系統的初始狀态 x0
每個時間的測量 Z
系統模型和測量模型
求解:
狀态x随着時間變化而産生的值
預測是這樣一個問題:
已知:
上一個狀态的更新值
上一個狀态的更新值和真實值之間的誤差
這一個狀态的預測值
這一個狀态的預測值和真實值之間的誤差
過程包括兩個方面:
一、由上一個更新值 Xk-1|k-1 預測這一個預測值 Xk|k-1
二、由上一個更新值和真實值之間的誤差 Pk-1|k-1 預測下一個預測值和真實值之間的誤差 Pk|k-1
具體來說,就是以下兩個方程。
(預測狀态) (5)
(預測估計協方差矩陣) (6)
這裡:
Xk-1|k-1 這種記法代表的是上一次的更新值,後面一個 k-1可以看做 Zk-1, 也就是上一次經過對比Zk-1(實際就是更新)之後所估計出的狀态Xk-1。
Xk|k-1 這種記法代表這一次的預測值, 同理于剛才的介紹, 經過上一次Zk-1之後所估計出的狀态Xk。
預測公式-預測狀态
也就是公式(5), 可以直接由系統模型導出。
預測公式-協方差矩陣:
P代表着估計誤差的協方差,代表着一種 confidence ,比如先驗估計誤差(預測值與真實值之間誤差)的協方差
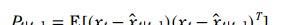
注:
方差有兩種形式
協方差的定義:
如果說方差是用來衡量一個樣本中,樣本值的偏離程度的話。協方差就是用來衡量兩個樣本之間的相關性有多少,也就是一個樣本的值的偏離程度,會對另外一個樣本的值偏離産生多大的影響,協方差是可以用來計算相關系數的,相關系數P=Cov(a.b)/Sa*Sb, Cov(a.b)是協方差, Sa Sb 分别是樣本标準差。【可以參考另一篇部落格《了解協方差》】
cov(x,y) = E( (x-u)(y-v)' ) = E(xy' - xv' - uy' + uv') = E(xy') - E(xv') - E(uy') + E(uv') = E(xy') - uv' - uv' + uv' = E(xy') - uv'
比較(5)和(1), 相減:
由于 狀态估計誤差 和 系統噪聲 是不相關的
如果随機變量 x和y是不相關的, 那麼
Cov(x,y) = 0 => E( (x-ex)(y-ey)' ) = 0 => E(xy') - ex*ey' = 0
如果 ex 和ey為0 => E(x,y') = 0 就像上面的情況, 誤差和噪聲都服從正态分布,是以期望都是0 .
獨立的充要條件:P(xy) = P(x)P(y)
更新過程實際上就是一下問題:
由上一個更新值得到的目前的預測值。
目前的觀測值
觀測模型
融合了預測值和觀測的更新值
由預測值的估計誤差得到更新值的估計誤差
更新方程如下:
其中K稱為kalman增益, 就像一個補償,決定着預測值應該變化多少幅度,才能變成更新值。
先看一個簡單的例子,從這個例子中來推導出這三個方程。
有一個直線軌道, 軌道上有一個火車,從火車站出發, 在t時刻,火車想要知道自己距離火車站的位置,可以有兩個資訊來源:
根據 t-1時刻的狀态資訊,以及一些控制資訊來推斷, 狀态包括 t-1時刻的位置、速度等, 控制資訊包括司機刹車、加速等等。
根據 t時刻的測量資料來推斷, 這裡假設車上有一個聲波發射器,可以探測到發射到火車站需要多少時間,進而得到離車站的距離。
要想得到一個比較好的結果,顯然不能隻依靠某一種方法來推斷,而 Kalman Filter的方法是:
首先, 利用t-1時刻進行推斷, 這一步叫預測。
然後, 利用t時刻的measurement 也可以推斷, 使用這個推斷對預測進行校正, 這一步叫更新。
t=0的時候, 火車狀态如 Figure.2 ,這時候, 火車的位置是比較準确的。
t=1的時候, 火車的預測狀态如 Figure.3 可以看到, 位置的方差變大了。
火車的預測主要遵循 式(1),而預測的方差在不斷變大,也就是說預測的準确度在下降, 這是由累積誤差 w 導緻的。
t=1 的時候,我們還有 measurement ,同樣可以推斷火車的位置,見下圖中的藍色的pdf
将兩個pdf相乘,得到下圖中的綠色pdf, 綠色pdf中較高的位置, 意味着預測和測量對這個位置都比較支援。
這裡有一個高斯分布的一個重要性質就是,兩個高斯分布的乘積還是高斯分布。
This is critical as it permits an endless number of Gaussian pdfs to be multiplied over time, but the resulting
function does not increase in complexity or number of terms; after each time epoch the new pdf is fully represented by a Gaussian function. This is the key to the elegant recursive properties of the Kalman filter。
紅色的pdf是預測的火車位置, 方程如下:
藍色的pdf是測量的火車位置, 方程如下:
綠色的pdf二者融合的或者位置, 方程如下:
寫成如下形式:
這兩個式子,就是kalman濾波的更新方程
但是,這隻是一個很特殊的例子,因為這裡假設預測和測量都是采用同樣的坐标系
更現實的情況是二者需要統一到一個 domain 中
比如上面所舉的例子中:
預測的時候, 預測值是用米作為機關的。
但是當測量的時候, 測量得到的值是用聲波經過的秒數作為機關的。
必須先要把兩個量統一到同一個domain才能進行融合。
比如上式子中, y2 (measurement)實際是聲波傳遞時間的一個正态分布,也就是說機關是秒。
一般做法是把
預測值 => 測量值
y1就變成:
y2不變:
這樣兩個坐标系都在 mesaurement domain 了。
兩個pdf所在坐标系的橫軸都是表示時間,而且以秒為機關了。
`
統一domain之後,更新方程就有了如下形式
将
H = 1/c
K =
代入,得到
這裡的H就相當于觀測方程中的H, K就是卡爾曼增益。
類似地, 融合之後的方差更新變成了
各個變量對應的情況如下:
最終的更新方程
Talk is cheap, show me the code.
<code>plot(t,x_update,'r',t,z,'g',t,x_true,'b');</code>
<code></code>
<code>本文轉自莫水千流部落格園部落格,原文連結:http://www.cnblogs.com/zhoug2020/p/7632853.html,如需轉載請自行聯系原作者</code>