場景:一個賭局,你跟莊家。你出 1 元,莊家出 0.96元。賭金數目可随之翻倍。
根據每次抛色子的結果的單雙決定勝負。
勝者得到雙方所下的賭金,計 1.96 元。
問題:如何下注才能做到,風險最小,盈利最大呢?
答案:凱利公式。
凱利公式的作用: 根據賠率與勝率,得出你每次的資金下注比例
公式的形式: 1 + 賠率 - 1/勝率
凱利公式最初為 AT&T 貝爾實驗室實體學家約翰·拉裡·凱利根據同僚克勞德·艾爾伍德·香農於長途電話線雜訊上的研究所建立。凱利說明香農的資訊論要如何應用於一名擁有内線消息 的賭徒在賭馬時的問題。賭徒希望決定最佳的賭金額,而他的内線消息不需完美(無雜訊),即可讓他擁有有用的優勢。凱利的公式随後被香農的另一名同僚 愛德華·索普應用於二十一點和股票市場中。
下面利用凱利公式對賭局進行模拟:
賠率
0.96
勝率
0.5
0.6
0.7
0.75
資金比
-0.02
0.183
0.388
0.49
由上表可知,沒得玩!!
凱利公式計算的結果本質是盈利率的數學期望,不難得出這樣一個結論:一切盈利率的數學期望為負的賭局,絕對不能參與!!
我們看到:就算你的勝率占到一半(0.5),但是因為賠率隻有0.96,不是1(亦即1:1,意為1賠1),是以你的期望才是負數!!!
賠率這麼低,那這個賭局還有沒有的玩了呢?
隻一個辦法,提高勝率!
勝率0.6,即為10中6
考慮三種可能的情況: 1)四連虧再六連中 2)虧中相間 3)六連中再四連虧
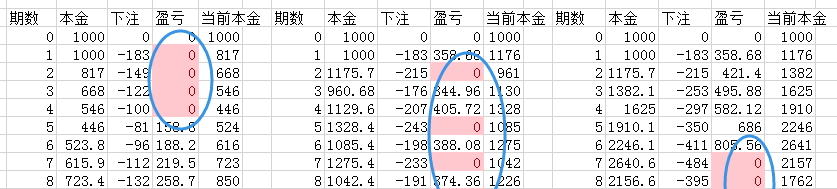
勝率0.7,即為10中7
考慮三種可能的情況: 1)三連虧再七連中 2)虧中相間 3)七連中再三連虧
勝率0.75,即為12中9
考慮三種可能的情況: 1)三連虧再九連中 2)虧中相間 3)九連中再三連虧
不利用凱利公式,則說明資金管理混亂。
比如你有1000,
第一次投一半:500,不中。
第二次還投500,這時候你遇到了很壞的情況,還不中。
你爆倉了!你出局了!
當然,你會說,那我補倉。那就屬于本文議題之外的問題了。
但是可以肯定一點:不管你補多少次倉,結果都是一樣的。
也許你還會說,我的運氣不會那麼背,不會前兩局都輸。這點我嚴重同意!
但是長期來看,總會有壞運氣找到你:連續四五期不中,拿走你以前的好運氣所得,甚至翻倍拿走。
唯有凱利公式可以避免這種情況!!!
本文要點:凱利公式得出的資金比例是每次你現有資金的比例,不是初始資金比例
不難發現,在數學期望為正的情況下,運用凱利公式進行資金管理,可以穩定盈利。
在相同的勝率下,如果不利用凱利公式進行資金管理,不能保證盈利。
我想,其中一個主要的原因是:資金不足,爆倉出局!
本文轉自羅兵部落格園部落格,原文連結:http://www.cnblogs.com/hhh5460/p/5129046.html,如需轉載請自行聯系原作者