前言
前幾篇文章介紹了線性回歸算法,線性分類模型分為判别式模型和生成式模型,本文首先簡單複習了與算法相關的數學基礎知識,然後分析各線性判别式分類算法,如最小平方法,Fisher線性判别法和感覺器法,最後總結全文。
1、相關的數學知識回顧
2、判别式模型和生成性模型
3、最小平方法
4、Fisher線性判别函數
5、感覺器算法
6、總結
1、直線方程和平面方程
拓展到分類思想:直線l為分類決策方程,坐标點落在直線l上方時,則分類為C1;坐标點落在直線l下方時,則分類為C2(如下圖)。
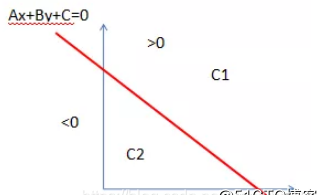
平面方程類似,在這裡不展開。
2、點到直線和點到平面的距離
點到直線的距離:
點到平面的距離
拓展到分類思想:平面方程為決策方程,正确分類的情況下,當點P到決策方程的距離越大,則分類模型越好;錯誤分類的情況下,點P到決策方程的距離作為損失函數,損失函數最小化過程即是模型參數最優化過程。
3、向量内積的數學意義
幾何意義:向量A與向量B的内積等于向量A在向量B的投影與向量B的乘積,當向量B是機關向量時,則等于向量A在機關向量方向的投影,機關向量類似于基函數或者可以了解成坐标軸,即向量A在向量B的投影可了解成向量A在向量B方向的坐标,如下圖,B'是B在OA坐标軸方向的投影。
拓展到分類思想:C1與C2屬于不同的類,給定一條決策性直線l,當C1與C2在直線L2的投影間距越大,則分類效果越好。增加不同類間的距離可以作為模型參數優化的方向。
如下圖,C1和C2的在直線L2的投影距離|C1"C2"|大于|C1'C2'|,是以決策方程直線L2優于直線L1.
4、梯度下降法
函數f(x0,x1,...,xn)在梯度方向是函數值變化(增加或減少)最快的方向(本文隻給出結論,後續文章會有詳細的說明)。
拓展到分類思想:損失函數最小化過程即是模型參數最優化過程,損失函數最小化可通過梯度下降法來實作,當疊代到一定程度,損失函數收斂,則疊代結束,參數w即是要求的最優參數。
流程圖如下:
我們常把分類問題分成兩個階段:推斷階段和決策階段,對于輸入變量x,分類标記為Ck。推斷階段和決策階段具體表示為:
推斷階段:估計P(x,Ck)的聯合機率分布,對P(x,Ck)歸一化,求得後驗機率P(Ck|x)。
決策階段:對于新輸入的x,可根據後驗機率P(Ck|x)得到分類結果。
判别式模型和生成性模型的差別
判别式模型:簡單的學習一個函數,将輸入x直接映射為決策,稱該函數為判别式函數。
生成式模型:推斷階段确定後驗機率分布,決策階段輸出分類結果,生成式模型包含兩個階段。
本文介紹判别式線性分類模型的三種算法。
最小平方法與最小二乘法的算法思想類似,K類判别函數由K個方程決定,
訓練集
,K類判别函數為
,k=1,2,...,K
參數矩陣為
,目标矩陣
。
求得最優參數w後,輸入變量x所屬K類的判别方法如下:
第一節講到,若兩個類在同一個決策方程的投影距離相隔越大,則該決策方程越好。再深入一點,相同類投影到決策方程的方差越小,則該決策方程越好,方差代表類投影到決策方程的聚集程度。這就是Fisher線性判别法參數優化思想。
參數優化思想:同類樣本投影到決策方程的方差最小,不同類樣本投影到決策方程的均值間隔最大。用表達式J(w)表示,J(w)越大越好。
如下圖:
其中,m1,m2分别表示不同類在決策方程的投影均值;S1,S2分别表示不同類投影到決策方程的方差。
求得最優參數w後,輸入變量x所屬類的判别方法如下:
感覺器算法的目的是找到能夠準确分離正負樣本訓練資料集的超平面。
超平面定義:
感覺器學習政策:
對訓練資料集某一樣本點(x,y),若wx+b>0,則y=1;若wx+b<0,則y=-1;
即感覺機模型為:
是以,對于誤分類的資料(xi,yi)來說:
是以,感覺器學習政策是最小化誤分類點到平面S的距離,不考慮分母項。
假設訓練資料集有M個誤分類點,損失函數為:
運用梯度下降算法最小化損失函數L(w,b)。
設學習率η,感覺器學習政策步驟:
(1)、選取處置w0,b0;
(2)、選取訓練集(xi,yi);
(3)、如果yi(w*xi+b)<=0,則更新權值參數w,b:
(4)、轉至(2),直至訓練資料集沒有誤分類點,得到超平面最優參數w,b。
感覺機學習算法由于采用不同的初值或選取不同的誤分類點,參數解可能不同(例題可參考《統計學習方法》)。
是以,對某一輸入點,若感覺機模型大于0,則分類為1;反之分類為-1。
本文介紹了線性判别分類的三種方法,第一種判别方法是根據點到判别函數的距離來分類,,第二種方法是根據輸入樣本在判别函數的投影距離進行分類,第三種方法則采用感覺機模型進行分類。
參考
Christopher M.Bishop <<Pattern Reconition and Machine Learning>>
李航 《統計學習方法》