本文目的
最近溫習了一下C++ STL中的algorithm庫函數,記得上次看這些内容時,還在讀書,可以追溯到2009年春天了(剛好4年J)。正所謂為“溫故而知新,可以為師矣”。閑話少說,開始正文。
算法庫
C++标準算法庫中包含一些模版函數,用于執行基本的算法,比如for_each(周遊容器),random_shuffle(随機打亂容器)等。主要實作包含在頭檔案<algorthim>中,少量在<numeric>中。它是STL的三大核心元件之一,其他兩個是容器(container,常用資料結構)和疊代器(Iterator,資料結構通路擴充卡)。設計思想:算法函數通過疊代器作用在容器上,最大程度的複用。比如for_each函數,可以通過疊代器作用在set,map,list,vector,deque等容器上。
所有的算法都會接受容器的疊代器作為參數,而不是容器本身,這樣算法可以作用于全部或者部分容器中的元素,十分靈活。如果算法(比如std::transform)需要通路兩個容器,一般傳入第一個容器的第一個元素,第一個容器的最後一個元素和第二個容器的第一進制素。不需要傳入第二個容器的最後一個元素,因為可以通過第一個容器的兩個疊代器計算出來。除非此算法允許作用在兩個不一樣長度的容器上,比如search函數。
為了使容器算法函數具有更高的靈活性,一般算法函數會接受一個函數或則函數對象(類似javascript的回調函數),這個函數在算法執行過程中内部使用,執行特殊的業務邏輯。
算法函數還有一個規律是具有兩種字尾,
字尾_if 此字尾的函數一般有一個沒有字尾的版本與之對應。如find和find_if,前者接受一個值,根據該值尋找容器中對應的元素,後者接受一個函數或函數對象(operator()必須傳回bool,辨別是否比對)。
字尾_copy 此字尾用于将算法修改後的元素拷貝到一個新的容器中,原始容器不被修改,是以此算法需要更多的記憶體。
疊代器範圍(Range)
STL的疊代器尊首一個原則:前閉後開,[first, last)。容器begin函數傳回的疊代器表示容器中的第一個元素,而end函數傳回的疊代器最後一個元素後面的位置(the one after the last element),也就是說*(end)沒有意義,*(end-1)表示最後一個元素。這樣有幾個好處:1)統一辨別容器結尾;2)計算疊代器距離時,不用額外加1。
示例
為什麼要使用算法函數。然道不能用C++的基本文法完成同樣的功能嗎?答案是肯定的,算法庫中的所有功能均可以使用最原始的C++文法實作,但是為什麼要重複造輪子呢?而且,算法庫提供而外的好處:1)代碼簡潔優雅,便于閱讀和維護;2)大多數算法會比你實作的效率更高(由C++委員會的大牛們實作的,能不快嗎?);3)更靈活,使用模版和疊代器風格,可以适配不同類型的資料類型和容器類型。
代碼最優說服力,看看下面的例子吧!計算pearson系數,一種計算兩個向量是否線性相關。取值範圍[-1, 1],絕對值越大,越相關,-1代表線性遞減,1代表線性遞增,0代表線性無關。計算公式如下:
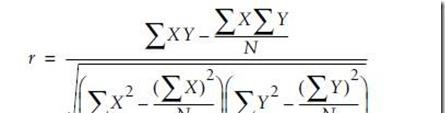
看看下面的代碼:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
<code>#include <algorithm></code>
<code>#include <numeric></code>
<code>#include <vector></code>
<code>#include <iostream></code>
<code>#include <cmath></code>
<code>using</code> <code>namespace</code> <code>std;</code>
<code>/**</code>
<code> </code><code>* calculate person without STL style</code>
<code> </code><code>*/</code>
<code>template</code><code><</code><code>class</code> <code>T1,</code><code>class</code> <code>T2></code>
<code>double</code> <code>pearson(</code><code>const</code> <code>vector<T1>& col1,</code><code>const</code> <code>vector<T2>& col2) {</code>
<code> </code><code>int</code> <code>n = col1.size();</code>
<code> </code><code>double</code> <code>xy_sum = 0;</code>
<code> </code><code>for</code><code>(</code><code>int</code> <code>i = 0; i < n; ++i) {</code>
<code> </code><code>xy_sum += col1[i] * col2[i];</code>
<code> </code><code>}</code>
<code> </code><code>double</code> <code>x2_sum = 0;</code>
<code> </code><code>x2_sum +=</code><code>pow</code><code>(</code><code>static_cast</code><code><</code><code>double</code><code>>(col1[i]),2);</code>
<code> </code>
<code> </code><code>double</code> <code>x_sum = 0;</code>
<code> </code><code>x_sum += col1[i];</code>
<code> </code><code>double</code> <code>y2_sum = 0;</code>
<code> </code><code>y2_sum +=</code><code>pow</code><code>(</code><code>static_cast</code><code><</code><code>double</code><code>>(col2[i]),2);</code>
<code> </code><code>double</code> <code>y_sum = 0;</code>
<code> </code><code>y_sum += col2[i];</code>
<code> </code><code>double</code> <code>deno =</code><code>sqrt</code><code>((x2_sum - 1.0 *</code><code>pow</code><code>(x_sum, 2) / n)*(y2_sum - 1.0 *</code><code>pow</code><code>(y_sum, 2) / n));</code>
<code> </code><code>return</code> <code>(xy_sum - 1.0 * x_sum * y_sum / n)/ deno;</code>
<code>}</code>
<code> </code><code>* STL Style for pearson</code>
<code>template</code><code><</code><code>class</code> <code>InputIt1,</code><code>class</code> <code>InputIt2></code>
<code>double</code> <code>person_stl(InputIt1 firstX, InputIt1 lastX, InputIt2 firstY) {</code>
<code> </code><code>int</code> <code>n = distance(firstX, lastX); </code>
<code> </code><code>double</code> <code>xy_sum = inner_product(firstX, lastX, firstY, 0);</code>
<code> </code><code>double</code> <code>x2_sum = inner_product(firstX, lastX, firstX, 0);</code>
<code> </code><code>double</code> <code>y2_sum = inner_product(firstY, firstY + n, firstY, 0);</code>
<code> </code><code>double</code> <code>x_sum = accumulate(firstX, lastX, 0);</code>
<code> </code><code>double</code> <code>y_sum = accumulate(firstY, firstY + n, 0);</code>
<code>int</code> <code>main(</code><code>int</code> <code>argc,</code><code>char</code><code>** argv) {</code>
<code> </code><code>vector<</code><code>int</code><code>> col1,col2;</code>
<code> </code><code>for</code> <code>(</code><code>int</code> <code>i = 0; i < 10; ++i) {</code>
<code> </code><code>col1.push_back(i);</code>
<code> </code><code>col2.push_back(10-i);</code>
<code> </code><code>cout <<</code><code>"Normal Style : "</code> <code><< pearson(col1,col2) << endl;</code>
<code> </code><code>cout <<</code><code>"STL Style : "</code> <code><< person_stl(col1.begin(),col1.end(),col2.begin()) << endl;</code>
<code> </code><code>return</code> <code>0;</code>
采用了兩種方法實作了pearson系數,第一種采用的C++原始文法實作。第二種采用STL風格,可以看到前者用去了25行,而後者不到10行。
輸出結果如下:
參考資料
<b>聲明:如有轉載本博文章,請注明出處。您的支援是我的動力!文章部分内容來自網際網路,本人不負任何法律責任。</b>
本文轉自bourneli部落格園部落格,原文連結:http://www.cnblogs.com/bourneli/archive/2013/03/22/2975756.html,如需轉載請自行聯系原作者