基數排序與本系列前面講解的七種排序方法都不同，它不需要比較關鍵字的大小。
它是根據關鍵字中各位的值，通過對排序的N個元素進行若幹趟“配置設定”與“收集”來實作排序的。
不妨通過一個具體的執行個體來展示一下，基數排序是如何進行的。
設有一個初始序列為: R {50, 123, 543, 187, 49, 30, 0, 2, 11, 100}。
我們知道，任何一個阿拉伯數，它的各個位數上的基數都是以0~9來表示的。
是以我們不妨把0~9視為10個桶。
我們先根據序列的個位數的數字來進行分類，将其分到指定的桶中。例如：R[0] = 50，個位數上是0，将這個數存入編号為0的桶中。
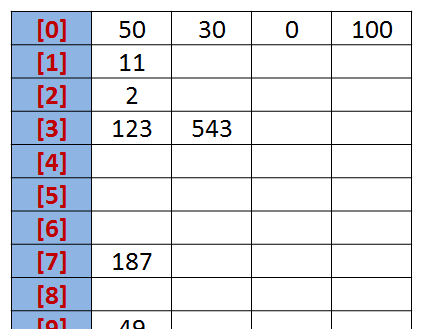
分類後，我們在從各個桶中，将這些數按照從編号0到編号9的順序依次将所有數取出來。
這時，得到的序列就是個位數上呈遞增趨勢的序列。
按照個位數排序： {50, 30, 0, 100, 11, 2, 123, 543, 187, 49}。
接下來，可以對十位數、百位數也按照這種方法進行排序，最後就能得到排序完成的序列。
（1）LSD法實作
實作代碼
<a></a>
package notes.javase.algorithm.sort;
public class RadixSort {
// 擷取x這個數的d位數上的數字
// 比如擷取123的1位數，結果傳回3
public int getDigit(int x, int d) {
int a[] = {
1, 1, 10, 100
}; // 本執行個體中的最大數是百位數，是以隻要到100就可以了
return ((x / a[d]) % 10);
}
public void radixSort(int[] list, int begin, int end, int digit) {
final int radix = 10; // 基數
int i = 0, j = 0;
int[] count = new int[radix]; // 存放各個桶的資料統計個數
int[] bucket = new int[end - begin + 1];
// 按照從低位到高位的順序執行排序過程
for (int d = 1; d <= digit; d++) {
// 置空各個桶的資料統計
for (i = 0; i < radix; i++) {
count[i] = 0;
}
// 統計各個桶将要裝入的資料個數
for (i = begin; i <= end; i++) {
j = getDigit(list[i], d);
count[j]++;
// count[i]表示第i個桶的右邊界索引
for (i = 1; i < radix; i++) {
count[i] = count[i] + count[i - 1];
// 将資料依次裝入桶中
// 這裡要從右向左掃描，保證排序穩定性
for (i = end; i >= begin; i--) {
j = getDigit(list[i], d); // 求出關鍵碼的第k位的數字， 例如：576的第3位是5
bucket[count[j] - 1] = list[i]; // 放入對應的桶中，count[j]-1是第j個桶的右邊界索引
count[j]--; // 對應桶的裝入資料索引減一
// 将已配置設定好的桶中資料再倒出來，此時已是對應目前位數有序的表
for (i = begin, j = 0; i <= end; i++, j++) {
list[i] = bucket[j];
}
public int[] sort(int[] list) {
radixSort(list, 0, list.length - 1, 3);
return list;
// 列印完整序列
public void printAll(int[] list) {
for (int value : list) {
System.out.print(value + "\t");
System.out.println();
public static void main(String[] args) {
int[] array = {
50, 123, 543, 187, 49, 30, 0, 2, 11, 100
};
RadixSort radix = new RadixSort();
System.out.print("排序前:\t\t");
radix.printAll(array);
radix.sort(array);
System.out.print("排序後:\t\t");
}
運作結果
排序前: 50 123 543 187 49 30 0 2 11 100
排序後: 0 2 11 30 49 50 100 123 187 543
排序類别
排序方法
時間複雜度
空間複雜度
穩定性
複雜性
平均情況
最壞情況
最好情況
基數排序
O(d(n+r))
O(n+r)
穩定
較複雜
通過上文可知，假設在基數排序中，r為基數，d為位數。則基數排序的時間複雜度為O(d(n+r))。
我們可以看出，基數排序的效率和初始序列是否有序沒有關聯。
在基數排序過程中，對于任何位數上的基數進行“裝桶”操作時，都需要n+r個臨時空間。
在基數排序過程中，每次都是将目前位數上相同數值的元素統一“裝桶”，并不需要交換位置。是以基數排序是穩定的算法。
本文轉自靜默虛空部落格園部落格，原文連結：http://www.cnblogs.com/jingmoxukong/p/4311237.html，如需轉載請自行聯系原作者
![查找算法之二分查找查找算法之二分查找[圖]](data:image/gif;base64,R0lGODlhAQABAIAAAP///wAAACwAAAAAAQABAAACAkQBADs=)