在上一節中我們知道了螢幕上一像素等于實際中多少機關長度(米或經緯度)的換算方法,而知道這個原理後,接下來我們要怎麼用它呢?它和我們前端顯示地圖有什麼關聯呢?這一節,我會盡量詳細的将這兩個問題一一回答。說一個題外話,這一系列的文章我都會少給代碼,多畫流程圖或者UML圖來跟大家交流,一來便于沒有很多GIS和程式設計基礎的人讀懂,二來使大家不局限于某種代碼的實作而更關注于原理。
我們之前反複提到了影像金字塔這個概念,但是沒有對其做一個大概的介紹,這裡我将這個概念補充一下。
現在,我假設我們的伺服器上有一個1G的影像,需要将其在前端進行顯示。我們傳統的做法就是首先将伺服器中的1G影像下載下傳到前端,然後浏覽器加載渲染出圖。但是大家想想,首先用戶端下載下傳1G的影像需要的時間一定是個漫長的過程,其次浏覽器加載這麼大的檔案也多半會導緻其崩潰。而最重要的一個問題是,我們的需求僅僅是浏覽全圖中的某一個區域下的某幾個級别,現在卻将全圖下載下傳完畢了,而這同樣還導緻了資料的不安全性(下載下傳到本地),同時我們的每一次放大和縮小以及拖拽都将會使浏覽器花上足夠長的時間去渲染。
可見,傳統的方式是不符合實際需求的。到後來,又有了新的解決方法,比如arcgis的IMS版本中提出了動态出圖的概念。也就是目前端發出的請求裡包含了需要顯示的範圍、顯示視窗的大小等參數後,背景動态的在原始資料中切出一個符合需求的瓦片,然後将這個資料傳回給前台,并且在伺服器中對這個瓦片做緩存。
但是,這個方法前端出圖依舊很慢,并且使地圖伺服器的壓力過大。終于,我們的影像金字塔解決方案出現了。
影像金字塔就是,我們首先将原始影像按照使用者的需求,比如使用者需要顯示多少種比例尺下的資料,需要顯示的是原始影像中的哪個區域的資料,将原始影像按照這些需求進行劃分和提取。如圖:
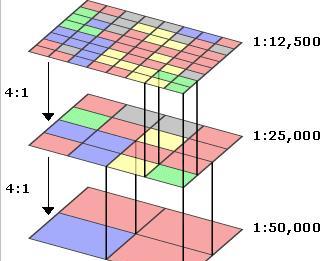
最低層就是我們提取和劃分出的比例尺最小的一級的瓦片,而最上層的則是比例尺最大的一級的瓦片。我們仔細觀察可以發現這樣的一個規律:比例尺越小的級别瓦片資料越少,反之則越大。而這個規律導緻的結果就是:比例尺越小的級别切圖的速度越快,同時,同樣大小的瓦片所包含的影像範圍越多。
當我們建立好了影像金子塔後,前端再請求地圖時,則将隻是在切好的瓦片緩存中,找到對應級别裡對應的瓦片即可。然後在前端将這些請求到的瓦片拼接出來,便可以得到使用者需要的級别下的可視範圍内的瓦片了。
上一節中我給出了影像圖切成離散型圖後檔案的組織形式,其中給大家展示了在這種切圖下,檔案的組織其實是按照瓦片的級别、行、列号來組織的。事實上,緊湊型瓦片(Bundle)的組織樣式也是如此,隻是它在得到了行列号後還要進行一系列換算,比如讀取索引檔案找到檔案中的偏移量等,這個換算方式我在以後的章節跟大家來讨論。并且,标準的WMS請求中也涉及到行列号的換算,WMS請求中有一個Bbox的參數,而這個參數也與行列号的換算有關系。而标準的WMTS請求中,TILEMATRIX、TILEROW、TILECOL這三個參數代表的就是瓦片的級别、行、列号。
由此可見,不管是針對哪種離線或線上的地圖的瓦片請求中,得到瓦片的level、col、row是請求能夠實作的核心。
下面,我們先給出瓦片行列号換算的公式。
假設,地圖切圖的原點是(x0,y0),地圖的瓦片大小是tileSize,地圖螢幕上1像素代表的實際距離是resolution。計算坐标點(x,y)所在的瓦片的行列号的公式是:
col = floor((x0 - x)/( tileSize*resolution))
row = floor((y0 - y)/( tileSize*resolution))
這個公式應該不難了解,簡單點說就是,首先算出一個瓦片所包含的實際長度是多少LtileSize,然後再算出此時螢幕上的地理坐标點離瓦片切圖的起始點間的實際距離LrealSize,然後用實際距離除以一個瓦片的實際長度,即可得此時的瓦片行列号:LrealSize/LtileSize。
如我在上一節《地圖比例尺換算原理》中描述的,當系統是經緯度系統時,此resolution可以直接使用切圖文檔中的resolution。如果系統是平面坐标系統時,此resolution的算法是:
resolution=scale*inch2centimeter/dpi。其中scale是地圖比例尺,inch2centimeter為英寸轉厘米的參數,dpi為1英寸所包含的像素。
現在我把實際的運用中的需求總結如下:
(1)得到畫布的高度和寬度以及此時需要顯示的地圖的幾何範圍
(2)得到畫布的高度和寬度以及此時需要顯示的地圖的幾何範圍,同時也得到了需要顯示的地圖的級别
最後,我們需要得到在這兩種需求下的瓦片行列号範圍。
針對在第3節中提到的兩種需求,我們進行了不同的換算過程,這裡我首先給出流程圖:
以下步驟中涉及到一些公共變量,為了便于描述,我這裡用英文代表一些參數。
originX,originY:地圖切圖時的切圖原點坐标。
tileSize:瓦片的螢幕像素大小。
Level:地圖級别。
resolution:某地圖級别下螢幕一像素代表的實際機關大小。
canvasWidth、canvasHeight:螢幕的長寬
geoMaxX、geoMinX:地理範圍中的最大即最小X坐标。
這個換算比較簡單,但是為什麼我們要首先換算這個中心點呢。原因是我們最後需要的真實地理範圍,并不一定是螢幕範圍所對應的那個地理範圍,它極有可能是大于這個螢幕地理範圍的。而事實上是,它一定是大于的,在後面我們講解瓦片圖層類的設計時,會提到一個地理範圍緩沖寬度,那時候大家就更能明白為什麼是要首先擷取地理範圍中的中心點了。
如果請求中已經指定了使用的Level,則我們接下來可以直接使用此Level來進行地圖實際請求範圍的換算。
而當請求中無Level時,我們的換算将會比較複雜一些,這個換算的目的就是求出此時的地圖應該以什麼Level顯示是最合适的,即nearestLevel。它的過程是,首先根據請求中的地理範圍和螢幕大小範圍,求得此時我們本需要的瓦片實際大小,即:(geoMaxX-geoMinX)/( canvasWidth/tileSize),也就是用實際地理長度除以此時的瓦片個數,進而得到了我們請求中本需求的瓦片實際大小。
但是,目前我們不能保證我們所切的圖中是一定有這個需求裡的比例尺的。于是我們還需要做一個周遊,周遊我們的地圖中所有的比例尺,找出一個與此需求比例尺下的瓦片實際大小最貼近的真實瓦片實際大小,而這個瓦片實際大小所對應的此時的地圖比例尺,即是我們求得到的最合适的比例尺,它所代表的地圖級别就是最貼近需求的地圖級别,nearestLevel。
在第一步中得到了centerGeoPoint,第二步得到了Level的條件下,這一步就很簡單了。
首先得到Level下的一像素代表的實際大小,即resolution。然後用centerGeoPoint加上或減去半個螢幕長度(canvasBounds)乘以resolution後得到的範圍便是需求中的螢幕範圍在獲得的Level下應該對應的實際地理範圍。
以螢幕左上角X所對應的實際地理坐标為例:
minX =centerGeoPoint - (resolution* canvasWidth)/2;
這裡順便提一下,算出的這個螢幕範圍所對應的地理範圍,它的作用是非常大的,在以後的螢幕坐标轉換成地理坐标,以及地理坐标轉換成螢幕坐标,還有偏移補償量的換算上是至關重要的一個參數。
這一步為收尾工作,根據之前算出來的一系列參數來進行最後的換算。
在知道了請求的地理範圍後,此起始行列号的換算便是水到渠成了。不過這裡還是要稍微做個補充,我們算出來的地理範圍并不能保證真實的瓦片的起始瓦片所對應的地理坐标與地理範圍的左上角地理範圍重合,為此我們應該允許地理範圍的一個擴張,這個擴張多少是一個很值得推敲的地方。這裡我們預設為擴張至請求到的第一張瓦片左上角所對應的地理坐标。
公式為:
fixedTileLeftTopNumX = Math.floor((Math.abs(originX - minX))/resolution*tileSize);
fixedTileLeftTopNumY = Math.floor((Math.abs(originY - maxY))/resolution*tileSize);
我們之前隻是求得了螢幕範圍所對應的地理範圍,而當我們換算出這個範圍所需要的瓦片後,這些算得的瓦片其所對應的地理範圍并不一定是螢幕範圍所對應的那個地理範圍,此時我們需要重新算出實際地理範圍。
realMinX = fixedTileLeftTopNumX * curLevelClipLength + originX;
realMaxY= originY - fixedTileLeftTopNumY * curLevelClipLength;
由于地理範圍中的第一張瓦片,即左上角的第一張瓦片,并不一定是完全包含在螢幕地理範圍内的,于是這裡又涉及到另外一對參數,左上角偏移像素。
為什麼要求這個參數呢,原因是,當我們把瓦片都請求回來後還要做一個換算,即換算出每一張瓦片的左上角坐标應該對應在圖層(TIleCanvas)上的哪一個螢幕坐标。這個偏移像素便是為了這個換算而做的準備。
offSetX = ((realMinX- minX )/resolution);
offSetY = ((maxY - realMaxY )/resolution);
再次補充,其中resolution表示的是此Level下的一像素所代表的實際機關大小。
這裡我先給出一個螢幕地理範圍與實際請求出的瓦片地理範圍間關系的示意圖:
在前面我已經訴說了,我們求得的螢幕地理範圍内的瓦片所代表的瓦片個數基本上是會比螢幕範圍本身是要大的。其實這個原因不難了解,因為瓦片是地圖表示的最小機關了,其不可能再劃分,是以在我們請求瓦片的起始行列号時,用到了Math.floor這個函數,即求得離螢幕範圍的左上角坐标最近的瓦片行列号。但是,在求得X、Y軸上的瓦片個數時,我們得用到Math.ceil這個函數,這是為了能求得離螢幕範圍的右下角坐标最近的瓦片行列号數。
具體公式是:
mapXClipNum = Math.ceil((canvasWidth + Math.abs(offSetX))/tileSize);
mapYClipNum = Math.ceil((canvasHeight + Math.abs(offSetY))/tileSize);
根據上面步驟,我們最後可以求出瓦片的行列号,以及需要的在X、Y軸的個數。同時我們還求得了将瓦片畫在畫布上時所需要的參數,左上角偏移像素。
這一節相信大家都會看的很累,因為這一節流程太多,公式太多,但是也正因為如此,這一節是我們介紹前端顯示地圖的系列中最重要的一節了,希望大家能和我一起将這個原理好好的揣摩與推敲。下一節裡我将寫的類容相對比較輕松了,主要介紹的會是我們算出了行列号後,如何使用它。我将對幾種常見線上地圖和離線地圖的請求方式做一個介紹和總結。歡迎大家持續關注。
今天是七夕,祝節日快樂。對和我一樣自己過節的人,寫句話和大家共勉:
在缺少思念的旅途
你是小船一隻,大橋一座。
如果您覺得本文确實幫助了您,可以微信掃一掃,進行小額的打賞和鼓勵,謝謝 ^_^