公衆号原文連結:檔案系統的靈魂資料結構 B樹 什麼是B-樹、B樹、B+樹、B*樹? 希望點進去的小夥伴關注一下我的公衆号喲,文末有二維碼,謝謝!
正如标題所言,本文介紹經常使我們混淆的B-樹、B樹、B+樹和B*樹。
首先,B-tree樹即B樹。B即Balanced平衡,因為B樹的原英文名稱為B-tree,而國内很多人喜歡把B-tree譯作B-樹,這是個非常不好的直譯,很容易讓人産生誤解,人們可能會以為B-樹和B樹是兩種樹。
不管是二叉樹、二叉查找樹還是平衡二叉樹,它們都有諸多限制,比如:
每個結點隻能存儲一個元素。
結點的度至多為2,即使是平衡二叉樹,在存儲百萬、千萬級别的資料量時,也會導緻樹的深度特别大,而深度大就會影響查找效率。
這裡提一下平衡二叉樹的缺點:
由于平衡二叉樹需要左旋和右旋來調整樹的結構,是以在頻繁插入和删除的場景下,每插入或删除一個結點,都極有可能導緻樹的不平衡,性能也會大打折扣。紅黑樹(後面會介紹)就是來解決這個問題的。
前面講的幾種資料結構,都是純記憶體操作,但是當資料量特别大(如資料庫中千萬級别的資料表、磁盤中的上萬個檔案等),記憶體都存不下了怎麼辦?在這種情況下,需要用外存(硬碟)來存儲,而對資料的處理則需要不斷地從硬碟調入調出。
此時,時間複雜度的計算就會發生變化,因為還要額外考慮對硬碟的通路次數和單次通路時間等。
為了降低對硬碟的通路次數,需要設計新的資料結構。前面講的幾種樹,結點都隻能存一個元素,是以,當元素非常多的時候,要麼結點的度非常大,要麼樹的深度非常大,這兩種情況都會導緻對硬碟的通路次數偏大。如果每個結點能存多個元素,那麼樹的總結點數就會大大減少,對磁盤的通路次數也會相應的大大減少。
由于有如上限制,為此引入了多路查找樹的概念。
多路查找樹:結點的度可以大于2,并且每一個結點可以存儲多個元素。由于是查找樹,是以結點之間存在某種特定的排序關系。
B樹是一種平衡的多路查找樹。
其實B樹和多路查找樹是一個意思,網上很多資料也是這樣認為的,但是也可以認為多路查找樹和B樹不是一個意思,因為多路查找樹不一定是平衡的。
B樹的階:所有結點中的最大孩子數。其實跟樹的度一個意思。
一個m階B樹的屬性:
如果根結點不是葉子結點,則其至少有兩顆子樹。
[m/2]<=k<=m,[m/2]為向上取整,比如9階B樹,5<=k<=9。每一個非根分支結點都有k個孩子和k-1個元素;葉子結點有k-1個元素。
所有葉子結點在同一層(平衡)。
所有分支結點有下列資訊資料:(n,A0,K1,A1,K2,A2,...,Kn,An),n是結點存儲的元素個數,Ai表示子樹,Ki表示元素,而從A0到An的值是從小到大排序的,這跟二叉查找樹的性質一樣。
下面來示範一下如何在B樹上查找元素,如下圖,是一顆B樹。
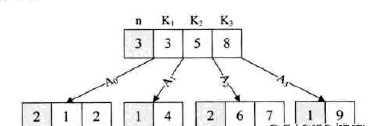
如果要查找元素7,首先從硬碟上讀取根節點(第一次讀磁盤)
即讀到了3,5,8三個元素,發現7并不在其中,但由于5<7<8,是以找到了A2,然後根據A2再讀取一次硬碟(第二次讀磁盤)
此時讀到了2,6,7三個元素,找到了元素7
兩次磁盤讀取就查找了我們想要的元素,非常高效,B樹就是這樣一種為内外存資料互動為設計的資料結構。
盡管B樹有很多好處,但是它還是有缺點的:
當進行範圍查找時,存在回旋查找的問題
排序的時候,需要進行一次中序周遊(order by)
其實這也是資料庫索引不使用B樹,而使用B+樹的原因。
因為B樹是存儲在磁盤中的,如下圖的B樹,假設每個結點都存儲在磁盤的不同頁中(一般在設計的時候,會将B樹的階與磁盤頁的大小相比對,目的是為了減少跨頁通路)。
那麼進行一次中序周遊的通路流程是:
頁面2->頁面1->頁面3->頁面1->頁面4->頁面1->頁面5
頁面1被通路了多次,這就是回旋通路問題。如果一個檔案系統使用B樹來做存儲結構的話,那性能肯定還是不高的。B+樹正是應檔案系統所需而出的一種B樹的更新版。
一顆B+樹的樣子如下圖所示。
圖1
一顆m階的B+樹與m階的B樹差異如下:
非葉子結點的元素個數=孩子個數
B+樹隻有達到葉子結點才命中(B-樹可以在非葉子結點命中)
所有的非葉子結點相當于葉子結點的索引,而所有的葉子結點才是存儲關鍵字的資料層
所有葉子結點根據關鍵字從小到大排序,且通過指針順序連接配接
所有非葉子結點中的元素,都同時存在于子節點中(是以元素個數與孩子數要相同,相同與将k個元素配置設定給k個孩子),在子節點中是最小(或最大)元素。
對于差異5,,什麼時候表現為最小元素,什麼時候表現為最大元素呢?
如圖1所示,根結點中元素與孩子指針按從小到大排序應該是
5<P1<28<P2<65<P3
然後分别将5配置設定給P1、28配置設定給P2、65配置設定給P3,自然而然就表現為了最小元素,二層的分支結點以此類推。
若要表現為最大元素,則需要将指針放在最前面,即類似于這樣的排序
P1<5<P2<28<P3<65
如果要在B+樹上查詢關鍵字,即使在分支結點上找到了該關鍵字,它也隻是用來做索引的,最終還是要定位到包含該關鍵字的葉子結點中。
大家有沒有注意到圖1還有一個data指針,它指向了最小葉子結點。如果我們要周遊整顆B+樹的話,直接從data指針開始搜尋即可,而不需要從根結點開始查找。
B*樹是B+樹的變體,在B+樹的非根分支結點再增加指向兄弟的指針,将結點的最低使用率從1/2提高到2/3。
一顆B*樹如下圖所示。
本文就介紹到這裡啦,感謝大家閱讀!
覺得寫得不錯的小夥伴,掃碼關注一下我的公衆号吧,謝謝呀!