前言
在量化金融中,我學習了各種時間序列分析技術以及如何使用它們。
通過發展我們的時間序列分析 (TSA) 方法組合,我們能夠更好地了解已經發生的事情,并對未來做出更好、更有利的預測。示例應用包括預測未來資産收益、未來相關性/協方差和未來波動性。
在我們開始之前,讓我們導入我們的 Python 庫。
讓我們使用pandas包通過 API 擷取一些示例資料。
基礎知識
時間序列是按時間順序索引的一系列資料點。——Wikipedia
為什麼我們關心平穩性?
平穩時間序列 (TS) 很容易預測,因為我們可以假設未來的統計屬性與目前的統計屬性相同或成比例。
我們在 TSA 中使用的大多數模型都假設協方差平穩。這意味着這些模型預測的描述性統計資料(例如均值、方差和相關性)僅在 TS 平穩時才可靠,否則無效。
“例如,如果序列随着時間的推移不斷增加,樣本均值和方差會随着樣本規模的增加而增長,并且他們總是會低估未來時期的均值和方差。如果一個序列的均值和方差是沒有明确定義,那麼它與其他變量的相關性也不是。”
話雖如此,我們在金融中遇到的大多數 TS 都不是平穩的。是以,TSA 的很大一部分涉及識别我們想要預測的序列是否是平穩的,如果不是,我們必須找到方法将其轉換為平穩的。(稍後會詳細介紹)
本質上,當我們對時間序列模組化時,我們将序列分解為三個部分:趨勢、季節性/周期性和随機。随機分量稱為殘差或誤差。它隻是我們的預測值和觀察值之間的差異。序列相關是指我們的 TS 模型的殘差(誤差)彼此相關。
我們關心序列相關性,因為它對我們模型預測的有效性至關重要,并且與平穩性有着内在的聯系。回想一下,根據定義,平穩TS的殘差(誤差)是連續不相關的!如果我們在我們的模型中沒有考慮到這一點,我們系數的标準誤差就會被低估,進而誇大了我們的 T 統計量。結果是太多的 1 類錯誤,即使原假設為真,我們也會拒絕原假設!通俗地說,忽略自相關意味着我們的模型預測将是胡說八道,我們可能會得出關于模型中自變量影響的錯誤結論。
白噪聲和随機遊走
白噪聲是我們需要了解的第一個時間序列模型(TSM)。根據定義,作為白噪聲過程的時間序列具有連續不相關的誤差,這些誤差的預期平均值等于零。對連續不相關的誤差的另一種描述是,獨立和相同分布(i.i.d.)。這一點很重要,因為如果我們的TSM是合适的,并且成功地捕捉了基本過程,我們模型的殘差将是i.i.d.,類似于白噪聲過程。是以,TSA的一部分實際上是試圖将一個模型适合于時間序列,進而使殘差序列與白噪聲無法區分。
讓我們模拟一個白噪聲過程并檢視它。下面我介紹一個友善的函數,用于繪制時間序列和直覺地分析序列相關性。
我們可以輕松地對白噪聲過程進行模組化并輸出 TS 圖檢查。
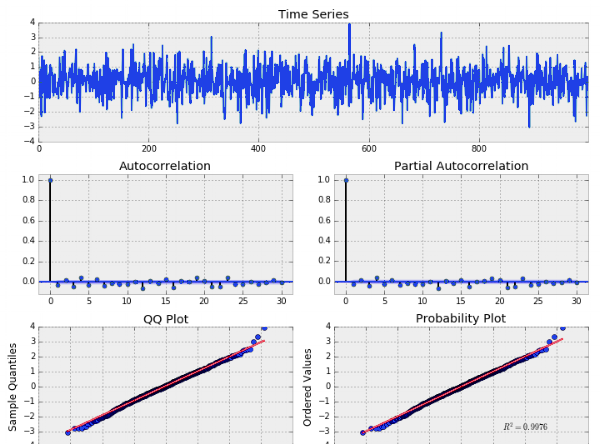
高斯白噪聲
我們可以看到該過程似乎是随機的并且以零為中心。自相關 (ACF) 和偏自相關 (PACF) 圖也表明沒有顯着的序列相關。請記住,我們應該在自相關圖中看到大約 5% 的顯着性,這是由于從正态分布采樣的純偶然性。下面我們可以看到 QQ 和機率圖,它們将我們的資料分布與另一個理論分布進行了比較。在這種情況下,該理論分布是标準正态分布。顯然,我們的資料是随機分布的,并且應該遵循高斯(正常)白噪聲。
随機遊走的意義在于它是非平穩的,因為觀測值之間的協方差是時間相關的。如果我們模組化的 TS 是随機遊走,則它是不可預測的。
讓我們使用“random”函數從标準正态分布中采樣來模拟随機遊走。
無漂移的随機行走
顯然,我們的 TS 不是平穩的。讓我們看看随機遊走模型是否适合我們的模拟資料。回想一下随機遊走是xt = xt-1 + wt。使用代數我們可以說xt - xt-1 = wt。是以,我們随機遊走系列的第一個差異應該等于白噪聲過程,我們可以在我們的 TS 上使用“ np.diff()” 函數,看看這是否成立。
随機行走的一階差分
我們的定義成立,因為這看起來與白噪聲過程完全一樣。如果我們對 SPY 價格的一階差分進行随機遊走會怎麼樣?
将随機行走模型拟合到ETF價格
它與白噪聲非常相似。但是,請注意 QQ 和機率圖的形狀。這表明該過程接近正态分布,但具有“重尾”。 ACF 和 PACF 在滞後 1、5?、16?、18 和 21 附近似乎也存在一些顯着的序列相關性。這意味着應該有更好的模型來描述實際的價格變化過程。
線性模型
線性模型又稱趨勢模型,代表了一個可以用直線作圖的TS。其基本方程為。
在這個模型中,因變量的值由β系數和一個單一的自變量--時間決定。一個例子是,一家公司的銷售額在每個時間段都會增加相同的數量。 讓我們來看看下面的一個特制的例子。在這個模拟中,我們假設堅定的ABC公司在每個時間段的銷售額為-50.00元(β0或截距項)和+25.00元(β1)。
線性趨勢模型模拟
在這裡我們可以看到模型的殘差是相關的,并且作為滞後的函數線性減少。分布近似正态。在使用此模型進行預測之前,我們必須考慮并消除序列中存在的明顯自相關。PACF 在滞後 1 處的顯着性表明自回歸 模型可能是合适的。
對數線性模型
這些模型與線性模型類似,隻是資料點形成了一個指數函數,代表了相對于每個時間步的恒定變化率。例如,ABC公司的銷售額在每個時間步長增加X%。當繪制模拟的銷售資料時,你會得到一條看起來像這樣的曲線。
模拟指數函數
然後我們可以通過采用銷售額的自然對數來轉換資料。現線上性回歸拟合資料。
指數函數的自然對數
如前所述,這些模型有一個緻命的弱點。它們假設連續不相關的誤差,正如我們線上性模型的例子中看到的那樣。在現實生活中,TS資料通常會違反我們的平穩假設,這使我們轉向自回歸模型。
自回歸模型 - AR(p)
當因變量針對自身的一個或多個滞後值進行回歸時,該模型稱為自回歸模型。公式如下所示:
AR (P) 模型
當您描述 模型的“階”時,例如階“p”的 AR 模型, p 表示模型中使用的滞後變量的數量。例如,AR(2) 模型或二階自回歸模型如下所示:
AR (2) 模型
這裡,alpha (a) 是系數,omega (w) 是白噪聲項。在 AR 模型中,Alpha 不能等于 0。請注意,alpha 設定為 1 的 AR(1) 模型是随機遊走 ,是以不是平穩的。
AR(1) 模型,ALPHA = 1;随機漫步
讓我們模拟一個 alpha 設定為 0.6 的 AR(1) 模型
AR(1) 模型,ALPHA = 0.6
正如預期的那樣,我們模拟的 AR(1) 模型的分布是正常的。滞後值之間存在顯着的序列相關性,尤其是在滞後 1 處,如 PACF 圖所示。
現在我們可以使用 Python 的 statsmodels 拟合 AR(p) 模型。首先,我們将 AR 模型拟合到我們的模拟資料并收益估計的 alpha 系數。然後我們使用 statsmodels 函數“order()”來檢視拟合模型是否會選擇正确的滞後。如果 AR 模型是正确的,估計的 alpha 系數将接近我們的真實 alpha 0.6,所選階數等于 1。
看起來我們能夠恢複模拟資料的基礎參數。讓我們用 alpha_1 = 0.666 和 alpha_2 = -0.333 來模拟 AR(2) 過程。為此,我們使用 statsmodel 的“generate_samples()”函數。該函數允許我們模拟任意階數的 AR 模型。
AR(2) 模拟 ALPHA_1 = 0.666 和 ALPHA_2 = -0.333
讓我們看看是否可以恢複正确的參數。
讓我們看看 AR(p) 模型将如何拟合 MSFT 對數收益。這是收益TS。
MSFT 對數收益時間序列
最好的階數是 23 個滞後或 23 !任何具有這麼多參數的模型在實踐中都不太可能有用。顯然,收益過程背後的複雜性比這個模型所能解釋的要複雜得多。
移動平均模型 - MA(q)
MA(q) 模型與 AR(p) 模型非常相似。不同之處在于 MA(q) 模型是過去白噪聲誤差項的線性組合,而不是像 AR(p) 模型這樣的過去觀察的線性組合。MA 模型的目的是我們可以通過将模型拟合到誤差項來直接觀察誤差過程中的“沖擊”。在 AR(p) 模型中,通過使用 ACF 對過去的一系列觀察結果間接觀察到這些沖擊。MA(q) 模型的公式是:
Omega (w) 是 E(wt) = 0 且方差為 sigma 平方的白噪聲。讓我們使用 beta=0.6 并指定 AR(p) alpha 等于 0 來模拟這個過程。
BETA=0.6 的模拟 MA(1) 過程
ACF 函數顯示滞後 1 很重要,這表明 MA(1) 模型可能适用于我們的模拟序列。當 ACF 僅在滞後 1 處顯示顯着性時,我不确定如何解釋在滞後 2、3 和 4 處顯示顯着性的 PACF。我們現在可以嘗試将 MA(1) 模型拟合到我們的模拟資料中。我們可以使用 “ARMA()” 函數來指定我們選擇的階數。我們調用它的“fit()” 方法來傳回模型輸出。
MA(1) 模型概要
該模型能夠正确估計滞後系數,因為 0.58 接近我們的真實值 0.6。另請注意,我們的 95% 置信區間确實包含真實值。讓我們嘗試模拟 MA(3) 過程,然後使用我們的 ARMA 函數将三階 MA 模型拟合到系列中,看看我們是否可以恢複正确的滞後系數(β)。Beta 1-3 分别等于 0.6、0.4 和 0.2。
BETAS = [0.6, 0.4, 0.2] 的模拟 MA(3) 過程
MA(3) 模型總結
該模型能夠有效地估計實際系數。我們的 95% 置信區間還包含 0.6、0.4 和 0.3 的真實參數值。現在讓我們嘗試将 MA(3) 模型拟合到 SPY 的對數收益。請記住,我們不知道真正的參數值。
SPY MA (3) 模型總結
讓我們看看模型殘差。
不錯。一些 ACF 滞後有點問題,尤其是在 5、16 和 18 處。這可能是采樣錯誤,但再加上重尾,我認為這不是預測未來 SPY收益的最佳模型。
自回歸移動平均模型 - ARMA(p, q)
ARMA 模型隻是 AR(p) 和 MA(q) 模型之間的合并。讓我們從量化金融的角度回顧一下這些模型對我們的意義:
AR(p) 模型試圖捕捉(解釋)交易市場中經常觀察到的動量和均值回歸效應。
MA(q) 模型試圖捕捉(解釋)在白噪聲項中觀察到的沖擊效應。這些沖擊效應可以被認為是影響觀察過程的意外事件,例如意外收益、恐怖襲擊等。
“對于雜貨店中的一組産品,在不同時間推出的有效優惠券活動的數量将構成多重‘沖擊’,進而影響相關産品的價格。” - AM207: Pavlos Protopapas, Harvard University
ARMA 的弱點在于它忽略了在大多數金融時間序列中發現的波動性聚類效應。
模型公式為:
ARMA(P, Q) 方程
讓我們用給定的參數模拟一個 ARMA(2, 2) 過程,然後拟合一個 ARMA(2, 2) 模型,看看它是否可以正确估計這些參數。設定 alpha 等于 [0.5,-0.25] 和 beta 等于 [0.5,-0.3]。
模拟 ARMA(2, 2) 過程
ARMA(2, 2) 模型總結
我們的真實參數包含在 95% 的置信區間内。
接下來我們模拟一個 ARMA(3, 2) 模型。之後,我們循環使用 p、q 的組合,以将 ARMA 模型拟合到我們的模拟序列中。我們根據哪個模型産生最低值來選擇最佳組合Akaike Information Criterion (AIC).
上面恢複了正确的階數。下面我們看到了在任何模型拟合之前模拟時間序列的輸出。
模拟 ARMA(3, 2) 系列,其中 Alpha = [0.5,-0.25,0.4] 和 BETAS = [0.5,-0.3]
ARMA(3, 2) 最佳模型總結
我們看到選擇了正确的階數并且模型正确地估計了我們的參數。但是請注意 MA.L1.y 系數;0.5 的真實值幾乎在 95% 的置信區間之外!
下面我們觀察模型的殘差。顯然這是一個白噪聲過程,是以最好的模型已經被拟合來解釋 資料。
ARMA(3, 2) 最佳模型殘差白噪聲
接下來,我們将 ARMA 模型拟合到 SPY 收益。下圖是模型拟合前的時間序列。
SPY收益率
我們繪制模型殘差。
SPY最佳模型殘差 ARMA(4, 4)
ACF 和 PACF 沒有顯示出顯着的自相關。QQ 和機率圖顯示殘差近似正态并帶有重尾。然而,這個模型的殘差看起來不像白噪聲,可以看到模型未捕獲的明顯條件異方差(條件波動性)的突出顯示區域。
自回歸綜合移動平均模型 - ARIMA(p, d, q)
ARIMA是ARMA模型類别的自然延伸。如前所述,我們的許多TS并不是平穩的,但是它們可以通過差分而成為平穩的。我們看到了一個例子,當我們采取Guassian随機遊走的第一次差分,并證明它等于白噪聲。換句話說,我們采取了非平穩的随機行走,并通過第一次差分将其轉變為平穩的白噪聲。
不用太深入地研究這個方程,隻要知道 "d "是指我們對序列進行差分的次數。順便提一下,在Python中,如果我們需要對一個序列進行多次差分,我們必須使用np.diff()函數。pandas函數DataFrame.diff()/Series.diff()隻處理資料幀/序列的第一次差分,沒有實作TSA中需要的遞歸差分。
在下面的例子中,我們通過(p, d, q)訂單的非顯著數量的組合進行疊代,以找到适合SPY收益的最佳ARIMA模型。我們使用AIC來評估每個模型。最低的AIC獲勝。
最好的模型的內插補點為 0 也就不足為奇了。回想一下,我們已經用對數價格的第一個內插補點來計算股票收益。下面,我繪制了模型殘差。結果與我們上面拟合的 ARMA(4, 4) 模型基本相同。顯然,這個 ARIMA 模型也沒有解釋序列中的條件波動!
拟合SPY收益的 ARIMA 模型
現在我們至少積累了足夠的知識來對未來的收益進行簡單的預測。這裡我們使用我們模型的predict() 方法。作為參數,要預測的時間步數需要一個整數,alpha 參數需要一個小數來指定置信區間。預設設定為 95% 置信度。對于 99%,設定 alpha 等于 0.01。
21 天SPY收益預測 - ARIMA(4,0,4)
自回歸條件異方差模型 - ARCH(p)
ARCH(p) 模型可以簡單地認為是應用于時間序列方差的 AR(p) 模型。另一種思考方式是,我們的時間序列 在時間 t的方差取決于對先前時期方差的過去觀察。
ARCH(1) 模型公式
假設系列的均值為零,我們可以将模型表示為:
零均值的 ARCH(1) 模型
模拟ARCH(1)過程
模拟ARCH(1)**2 過程
請注意 ACF 和 PACF 似乎在滞後 1 處顯示顯着性,表明方差的 AR(1) 模型可能是合适的。
廣義自回歸條件異方差模型 - GARCH(p,q)
簡單地說,GARCH(p, q) 是一個應用于時間序列方差的 ARMA 模型,即它有一個自回歸項和一個移動平均項。AR(p) 對殘差的方差(平方誤差)或簡單地對我們的時間序列平方進行模組化。MA(q) 部分對過程的方差進行模組化。基本的 GARCH(1, 1) 公式是:
GARCH(1, 1) 公式
Omega (w) 是白噪聲,alpha 和 beta 是模型的參數。此外 alpha_1 + beta_1 必須小于 1,否則模型不穩定。我們可以在下面模拟一個 GARCH(1, 1) 過程。
模拟 GARCH(1, 1) 過程
再次注意到,總體上這個過程與白噪聲非常相似,然而當我們檢視平方的eps序列時,請看一下。
模拟 GARCH(1, 1) 過程平方
顯然存在着自相關,ACF和PACF的滞後期的重要性表明我們的模型需要AR和MA。讓我們看看我們是否能用GARCH(1, 1)模型恢複我們的過程參數。這裡我們使用ARCH包中的arch_model函數。
GARCH 模型拟合摘要
現在讓我們運作一個使用 SPY 收益的示例。過程如下:
疊代 ARIMA(p, d, q) 模型的組合來拟合我們的時間序列。
根據 AIC 最低的 ARIMA 模型選擇 GARCH 模型階數。
将 GARCH(p, q) 模型拟合到我們的時間序列。
檢查模型殘差和殘差平方的自相關
另請注意,我選擇了一個特定的時間段來更好地突出關鍵點。然而,根據研究的時間段,結果會有所不同。
拟合SPY收益的 ARIMA(3,0,2) 模型的殘差
看起來像白噪聲。
拟合SPY收益的 ARIMA(3,0,2) 模型的平方殘差
平方殘差顯示自相關。讓我們拟合一個 GARCH 模型。
GARCH(3, 2) 模型拟合SPY收益
在處理非常小的數字時,會出現收斂警告。在必要時,将數字乘以10倍的系數以擴大幅度,可以起到幫助作用,但是對于這個示範來說,沒有必要這樣做。下面是模型的殘差。
拟合SPY收益的 GARCH(3, 2) 模型殘差
上面看起來像白噪聲。現在讓我們檢視平方殘差的 ACF 和 PACF。
我們已經實作了良好的模型拟合,因為平方殘差沒有明顯的自相關。