數數專題

目錄

​借助dp​

​​CF814E​​

​​AGC24E​​

​​AGC16F​​

​​小結​​

​​dp+複雜度平衡: loj547​​

​​dp+壓縮自動機: CF506E​​

​容斥原理​

​​naive題：51nod 1829​​

​​ZJOI2016 小星星​​

​​noiac2201 連續子序列: dp出容斥的貢獻​​

​組合意義轉化​

​​管道取珠​​

​​AGC13E​​

​​noiac 2448,2327​​

​奇技淫巧​

​​noiac 2034​​

注：尚未完成，先發出來，然後去睡覺

數數，是一個從出生就開始學并一直學不會的東西

這裡講“數數”，是指：形如“計算滿足xxx條件的方案數”的問題。

實作較複雜的問題會給代碼。剩下的可以在 vjudge/原網站 上翻我的送出記錄得到代碼

注：我一般喜歡交vjudge，并且我的常用号是 LightningUZ_CF 而不是 LightningUZ

有一些數數，比如 GF 相關，會另外講。

這裡講的主要是不用GF，用組合數，dp等技巧的數數題。

動态規劃是數數的好朋友，很多時候我們可以用動态規劃解決數數問題。

有人稱其為 “計數dp”。比如我們熟悉的背包，就是一種dp。

當然，和背包相關的dp，與數數的關系不大，不細展開。

來點例題：

參考了LCA的做法，他的題解在 ​​這裡​​

LCA的題解太神仙了，導緻我這個菜雞幾乎看一行式子睡一次覺，就為了想 “這裡為啥-1？” 這種事情，睡了4、5覺才做出來 是以這裡會仔細講（

這題是比較純正的dp，隻用到了非常少量的組合數學内容，全他媽在讨論

我們發現這條件還挺多：最短路唯一，最短路遞增，度數有限制，并且為 \(2\) 或 \(3\)。

“最短路遞增”，想象一下最後的最短路數組，相同的應該連續。那我們可以把連續的一段相同的劃開，稱為 “段”。

注意到，相鄰兩個段的最短路應該正好相差 \(1\)。并且後面一段的每個點都會有 恰好一條 到上一段的邊。

（如果沒有，那最短路就不對；如果有兩條以上，那最短路就不唯一）

段内部允許有邊。

看到分段，很容易想到dp。雖然粗略一想似乎不太會，但我們不用急，慢慢來。

别的不管，先設 \(f(i)\) 表示分到第 \(i\) 段的方案數，這個狀态怎麼也得有。

然後我們按套路，枚舉上一段的點 \(j\)，然後 \(f(j)\times w(j+1,i)\) 轉移過來。\(w\) 函數表示轉移系數。

仔細一想，這個轉移好像和段裡面有多少個點有很大的關系。那我們得再記一維表示點數。

\(f(i,j)\) 表示到第 \(i\) 段，最後一段分了 \(j\) 個點，方案數。

\(f(i,j)=\sum\limits_{k} f(i-j,k)\times w(...)\)

我們注意到這樣還不太能做，因為 \(2\) 度點和 \(3\) 度點處理起來不太一樣，是以這個 \(w\) 似乎不太能寫出來。

那就記一下上一層有多少個 \(2\) 度和 \(3\) 度的點，記為 \(c_2,c_3\)，然後考慮它們在自己那一層（即，上一層）内部，以及和目前的這一層，如何比對起來。

上一層的點數可以直接得知，就是 \(c_2+c_3\)。這一層的點數需要再記一下。

再一想，上一層的每個點到上上層都恰好有一條邊。那這麼說，\(2\) 度點其實隻有 \(1\) 個插頭，然後 \(3\) 度點有 \(2\) 個插頭。是以轉移函數的本質是要考慮這些 插頭的比對。

于是我們設這個轉移的函數為， \(g(n,c_2,c_3)\) 表示：

這一層有 \(n\) 個點，上一層有 \(c_2\) 個點有 \(1\) 個插頭， \(c_3\) 個點有 \(2\) 個插頭；

上一層的更前面已經滿足了限制，并且上一層到上上層的邊已經連好了；

我們要考慮，上一層内部的比對，以及上一層與下一層的比對；

的方案數。

容易寫出轉移：\(f(i,j)=\sum\limits_{k} f(i-j,k)\times g(j,c_2,c_3)\) （\(c_2,c_3\) 很容易統計出來）

最後的答案就是 \(\sum\limits_{j} f(n,j)\times g(0,c_2,c_3)\)。

那我們把 \(g\) 搞出來就做完了。但是這個 \(g\) 看起來比較複雜，分情況讨論

以下稱 “\(A\)” 表示隻有一個插頭的點，\(B\) 表示有 \(2\) 個插頭的點

\(n=0\)此時下一層沒有點，那就隻需要考慮層内的比對

\(c_2=0\)，\(c_3>0\)

此時隻有 \(B\) 點，那這樣比對一波，一定會形成若幹個環。

我們枚舉其中一個環來轉移。

為了避免算重複，我們強制讓枚舉的那個環包含 \(B\) 點中标号最小的那個。

由于不能有重邊和自環，環長至少為 \(3\)

得到轉移： \(g(0,0,c_3)=\sum\limits_{i=3}^{c_3} N(i)\times \binom{c_3-1}{i-1}\times g(0,0,c_3-i)\)

其中 \(N(i)\) 表示 項鍊數，也就是排一個環的方案數。

組合數裡面的 \(-1\) 是因為我們已經選好一個，接下來隻要選 \(i-1\) 個

\(c_2,c_3>0\)

此時 \(A,B\) 點都有。我們考慮連一條邊，這條邊可能連接配接着：

\(A+A\)，\(B+B\)，\(A+B\)

注意到我們不應該考慮 \(B+B\)，因為它要麼會在 \(g(0,0,*)\) 的時候被算到，要麼會在考慮完 \(A,B\) 插頭間的邊之後，其中一個 \(B\) 變成 \(A\)

是以我們隻需要考慮，一個 \(A\) 點和哪種點比對了

為了避免重複，還是要強制選 \(A\) 裡面編号最小的那個。

如果我們再選一個 \(A\)，那就有 \(c_2-1\) 種選法，并且兩個插頭都接起來，沒了。這一部分是 \((c_2-1)\times g(0,c_2-2,c_3)\)

如果我們選一個 \(B\)，那就有 \(c_3\) 種選法。而此時，\(A\) 點插頭沒了，而 \(B\) 點的插頭數從 \(2\) 個變成 \(1\) 個，也就便乘了 \(A\) 類點。于是 \(A\) 類點的數量并沒有變化，隻有 \(B\) 類點的數量少了一個。那這一部分是

\(c_3\times g(0,c_2,c_3-1)\)

綜上，\(g(0,c_2,c_3)=(c_2-1)\times g(0,c_2-2,c_3)+c_3\times g(0,c_2,c_3-1)\)

\(n>0\)

此時我們需要考慮下一層的比對

下一層的每個點都要找一個比對。為了避免重複，我們考慮下一層裡面标号最小的那個點和誰比對。

它可能和 \(A\) 類點比對，有 \(c_2\) 種選法，此時 \(A\) 類點少一個，\(B\) 類不變。即 \(c_2\times g(n-1,c_2-1,c_3)\)

它可能和 \(B\) 類點比對，有 \(c_3\) 種選法。此時有一個 \(B\) 類點變成 \(A\) 類點，是以是 \(B\) 少一個 \(A\) 多一個，即 \(c_3\times g(n-1,c_2+1,c_3-1)\)

綜上，\(g(n,c_2,c_3)=c_2\times g(n-1,c_2-1,c_3)+c_3\times g(n-1,c_2+1,c_3-1)\)

注意邊界 \(g(0,0,0)=1\)

然後就可以先預處理出 \(g\)，然後對着式子搞 \(f\)，然後對着式子搞答案。

總的複雜度是 \(O(n^3)\)，非常顯然。

​​代碼​​

這題是一個“計樹dp”，通常有一種套路：\(f(i,...)\) 表示 \(i\) 個點的樹，...，的數量。

不過這題，要搞出這顆“樹”要花一些功夫。

首先考慮一個問題，題目問的是本質不同的 序列組數量，而同一種序列組可能有不同的插入方案，如何去重？

我們發現，重複當且僅當我們插入的數有一堆連續的重複。比如aaabb要變成aaabbb。

此時我們強行插在最後一個位置，然後方案就是唯一的了。

由于我們要讓字典序遞增，再分析一下這種插入方式的性質，我們發現：每次插入進去的元素，要比“頂掉”的元素的字典序 嚴格 大。

為了避免邊界情況，我們令序列的最後有一個 \(0\)，并且我們不能插在 \(0\) 後面。那插入在最後的情況相當于是頂掉了 \(0\)，沒問題。

我們考慮每個數的 “流向”。即，我們畫一根線。當它被插進來的時候，就建立一個線頭。如果它沒有被頂掉，那這根線豎直向下，否則就斜着向右下。

比如說，序列組：

它的 “流向” 示意圖如下：

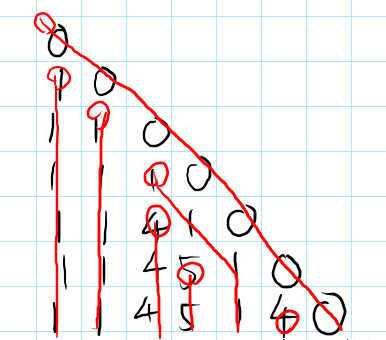
每個紅色的圈圈表示一個線頭的開始。用眼睛瞪這個圖，結合腦子想，發現：

0一定是一條斜線向下

每一個 “線頭” 一定比它上面的那個位置 嚴格 大（因為它要頂掉上面那個位置）

然後再一想，發現：我們可以把每個（0以外的）線頭和它上面那個位置所在的線頭連一條邊。這樣一定是顆樹（因為“嚴格大于”這個東西不可能有環，并且顯然連通）。我們考慮以 \(0\) 為根。

這顆樹會有很多個叉，但是它的點權值在樹上外向遞增（即，父親小于兒子）

考慮每個“線頭”被插入進來的時間，我們發現這玩意很顯然也遞增。

那我們給樹上的每個點兩個權值，一個表示插入時間，一個表示填的數字。我們發現，如果知道了每個點的插入時間，也知道它的父親，那我們其實就能唯一确定它去頂掉哪個點，再結合填的數字...我們就能唯一确定一個方案！（即，一個序列組）

于是變成了數樹問題。

考慮到倆權值要遞增，我們設 \(f(n,x)\) 表示，\(n\) 個點的樹，根節點權值是 \(x\)，方案數。答案是 \(f(n+1,0)\)。

考慮根的所有子樹，發現每個子樹的根的權值都 \(\ge x+1\)，并且一共有 \(n-1\) 個點。這是一個森林計數。

而我們發現“森林計數”和“樹計數”可以互相轉移！不妨換一下狀态，設：

\(f(n,x)\) 表示 \(n\) 個點的森林，每個樹的根的權值都 \(\ge x\)，方案數

\(g(n,x)\) 表示 \(n\) 個點的樹，根的權值是 \(x\)，方案數。

首先，\(g(n,x)=f(n-1,x+1...k)\)。我們用字尾和優化掉這個東西。

然後 \(f(n,x)=\sum\limits_{i=1}^{n} f(i,x)\times g(n-i,x)\times \binom{n}{i}\)。

這個很明顯，我們選出前面 \(i\) 個是森林，然後剩下的 \(n-i\) 個單獨構成一顆樹，就行了。

\(\binom{n}{i}\) 是因為我們要給它配置設定一個 “插入時間”。前面的 \(f,g\) 這樣合并不會算重是因為，雖然它會算重樹結構，但是此時的插入時間那一維不會重。

注意到這樣的 \(f\) 是至少兩棵樹的。我們給它加上 \(g(n,x)\) ，就把獨木成林的情況考慮到了。

然後就這樣轉移一波即可，答案是 \(g(n+1,0)\)

好家夥，剛數完樹，開始數DAG了

先拿SG函數做一波轉化，再考慮反面，相當于要數 \(SG(1)=SG(2)\) 的方案數。

然後我們考慮按 \(SG\) 的值把圖分層。

考慮把 \(S\) 中 \(SG=0\) 的那些點抽出來，發現：其餘每個點到它們至少一條邊，并且這些點内部不能有邊。

抽出來之後，把它們删掉，發現剩下的點裡面，整體 \(SG\) 都 \(-1\)，滿足同樣的性質，即，最優子結構。

于是考慮dp。設 \(f(S)\) 表示 \(S\) 中最小的兩個元素 \(SG\) 值相同的情況，\(U\) 表示全集，認為是 \(1...n\) 組成的集合。然後答案就是 \(2^m-f(U)\)

注意到 \(S\) 不能把 \(1,2\) 分開，否則這個dp狀态就不可用。然後枚舉 \(S\) 的子集 \(T\)，記 \(S/T\) 表示 \(S\cap (\overline{T})\)，即 \(S\) 去掉 \(T\) 的那一部分。

那麼 \(S/T\) 中每個點到 \(T\) 至少一條邊 （和上題挺像，少了度數限制），\(T\) 到 \(S/T\) 的邊可以瞎連，不影響。

\(T\) 内部的邊 全部不能連 ，而 \(S/T\) 内部的連邊通過 \(f\) 得到。

那就是 \(f(S)=\sum\limits_{T\subsetneqq S} f(S/T)\times w_1(T,S/T)\times w_2(S/T,T)\)

設 \(E(u,S)\) 表示 \(u\) 有多少出邊到 \(S\)。可得轉移函數：

\(w_1\) 表示瞎連方案數，\(w_1(S_1,S_2)=\prod\limits_{x\in S_1} 2^{E(x,S_2)}\)

\(w_2\) 表示連至少一條邊的方案數，把 \(w_1\) 的轉移變成 \(\prod (2^{...}-1)\) 就行了，很明顯 \(-1\) 就可以去掉不連的方案。

這兩個都可以每次預處理出 \(E\) 之後，掃一遍算出來。

于是總複雜度是 \(O(n\times 3^n)\)。

我們可以先研究一波問題的性質，把問題轉化成好做的形式，或者是提煉出我們真正需要知道的東西，再用dp做。

（接下來就開始飛了）

首先考慮一個naive dp:

設 \(f(i)\) 表示長度為 \(i\) ，滿足條件的01串個數。那麼： \(f(i)=2f(i-1)-f(i-m-1)\)。

這玩意有兩種搞法：

注意到 65537 是個 NTT 模數，對于 \(m\le 8192\) 的資料（我實作的不太精細，如果精細實作可以做到 \(m\le 32768\)），可以跑一個常系數齊次線性遞推，\(O(m\log m\log n)\)

當 \(m>8192\) 的時候，注意到 \(\dfrac{n}{m}\) 非常小。我們給這個遞推賦予組合意義：\(u\) 到 \(u+1\) 有 \(2\) 條重邊，\(u\) 到 \(u+m+1\) 有 \(-1\) 條重邊，求方案數。我們枚舉跳了多少條 \(+(m+1)\) 的邊，計算出跳了多少條 \(+1\) 的邊，然後用組合數瞎jr算一下方案數加起來就行；複雜度 \(O(\dfrac{n}{m})\)。

綜合兩種做法，就可以過了。

注意一個細節：做法1的遞推裡面，邊界是：當 \(i<m\) 時，\(f(i)=2^i\)；\(f(m)=2^m-1\)。

而 \(f(m)=2^m-1\) 是我們手動設定的，如果按做法2直接跑，得到的是 \(f(m)=2^m\)。容易發現，隻有這一位不對。

如何把它修正回來？（修正主義）

設做法2跑一個 \(n\) 得到的方案是 \(g(n)\)，也就是在DAG上從 \(0\) 跑到 \(n\) 的方案數。

一個很顯然的想法是，我們直接跑這個計數，相當于是給 \(f(m)\) 加了 \(1\) 之後做上面的遞推。不合法的部分，就是這個 \(f(m)\) 增加 \(1\) 之後的影響。考慮組合意義，這個影響就相當于在 DAG 上從 \(m\) 走到 \(n\) 的路徑數。由于這個DAG的邊隻和點的相對位置有關，是以這個方案數就是 \(g(n-m)\)。

是以我們得到 \(f(n)=g(n)-g(n-m)\)。

注意到 \(g(n+1)=2g(n)-g(n-m)\)，是以這個式子也等于 \(g(n+1)-g(n)\)。

不過我沒想明白它的組合意義。評論區大佬也可以講一下，如何形象一點的了解 \(g(n+1)-g(n)=f(n)\) 這件事情。

衆所周知，一些dp可以用自動機的語言寫出來，轉化成自動機上的數路徑問題

對于一個自動機，衆所周知，我們可以壓縮它

有以下幾種政策：

轉移邊有很多重合部分，把它壓起來，如SAM

有用的狀态數很少，如PAM （本質不同回文串 O(n) 個）

根據問題特點，改寫自動機，并按照上面兩個方法壓縮，如，本題

先寫一個 naive-dp。設 \(m=|s|\)，\(N\) 表示串的總長，即 \(n+m\)。

\(f(i,l,r)\) 表示長度為 \(i\) 的回文串，使得 \(s[l:r]\) 是它子序列的方案數。

每次考慮在串的兩邊加字元，并考慮它是 \(s_l,s_r\)，還是其它。然後讨論一波：

邊界：

如果 \(i=0\)，\(f(i,l,r)=[l>r]\)

如果 \(i=1\)，\(f(i,l,r)=[l\ge r]\)

如果 \(l>r\)，\(f(i,l,r)=26^{\lceil \frac{i}{2}\rceil}\)

轉移：

如果 \(s_l=s_r\)，\(f(i,l,r)=25f(i-2,l,r)+f(i-2,l+1,r-1)\)

如果 \(s_l\neq s_r\)，\(f(i,l,r)=24f(i-2,l,r)+f(i-2,l+1,r)+f(i-2,l,r-1)\)

然後 \(f(N,1,m)\) 就是答案了。

把狀态 \((i,l,r)\) 裡面的那個 \(i\) 看成是在走步（每次走兩步，分奇偶讨論下就行），并把 \((l,r)\) 建點。

如果 \(l>r\)，我們稱其為“結束點”，記作 \(E\) 類；如果 \(s_l=s_r\)，稱其為“相同點”，記作 \(A\) 類；否則稱為 “不同點”，記作 \(B\) 類。

我們把點排成方陣。\(A,B\) 構成一個上三角，\(E\) 都在左下角。

對角線上一定都是 \(A\)。

一個 \(A\) 點，它可以向左下角連一條邊；一個 \(B\) 點，它可以向正左/正右連一條邊。

每個點上都有自環。根據dp方程，\(A\) 點有 \(25\) 條自環，\(B\) 點有 \(24\) 條自環，\(E\) 點有 \(26\) 條自環。

我們從 \((1,m)\) 開始走，走到 \(E\) 點結束，可以走邊，可以走自環，走 \(N\) 步，問方案數。

暴力矩乘，\(O(m^6\log n)\)，過不去。

我們考慮壓縮這些點構成的自動機。注意到我們的 \(E\) 點隻需要兩條對角線，\(j=i-1\)，\(j=i-2\)，因為我們一定會走到這兩條線之一就停止。

根據這個，我們走一條路下來，\(r-l+1\) (長度) 肯定會從 \(m\) 變化到 \(0/-1\)。注意到，走一個 \(A\) 長度 \(-2\)，走一個 \(B\) 長度 \(-1\)。設我們走了 \(a\) 個 \(A\)，\(b\) 個 \(B\)，那麼 \(a=(m-b+1)/2\)

也就是說，确定了 \(b\) 就可以确定 \(a\)。

然後我們注意到，一條路徑的貢獻，隻和 \(a,b\) 有關，貢獻是 \(25^a\times 24^b\times 26/1\)，和經過的順序并沒有關系。

\(a,b\) 值相同的路徑可能有很多條，但是我們現在知道，本質不同隻要O(m)條

設 \(P(b)\) 表示經過了 \(b\) 個 \(B\) 的路徑條數。然後我們的自動機就隻需要關心 \(A,B\) 的數量了。

注意到我們怎麼也得經過一個 \(A\)，那麼 \(b\) 的值域是 \([0,m-1]\)，\(a\) 的值域是 \([1,(m+1)/2]\)

我們建出這樣的一個自動機：點 \(B_i\) 表示經過 \(i\) 個 \(B\) 對應的狀态，\(A_i\) 同理。

為了讓它倆能 “拼起來”，我們考慮把它倆對接，如下：

\(B_{m-1}\to B_{m-2}\to ... \to B_{1}\to A_{1}\to A_{2}\to ... \to A_{(m+1)/2}\)

每個 \(A_i\) 的下面再挂一個 \(E_i\) 表示結束。

每個 \(B\) 點有 \(24\) 個自環，\(A\) 點有 \(25\) 個自環，\(E\) 點有 \(26\) 個自環。

這樣，枚舉 \(b\)，計算出 \(a=(m-b+1)/2\)，\(B_b\) 到 \(E_a\) 的路徑就和原圖上的 本質不同路徑 一一對應了。

走一步相當于長度 \(+2\)。

如果 \(N\) 是偶數，把這個圖的鄰接矩陣搞出來求個 \(N/2\) 次幂，統計一下答案就行了。

如果 \(N\) 是奇數，稍微複雜些。

我們令最後一步的長度隻 \(+1\)。那我們會走 \((N+1)/2\) 步。

不合法，當且僅當從一個 \((x,x+1)\) 的 \(A\) 類點轉移到 \(E\)。因為它要做最後一步，但它需要加兩個相同字元，而我們強制讓最後一步隻加一個字元，就不能真正的比對上。

我們把這種情況減掉即可。手動推一推，發現這種情況下有 \(2a+b=m\)。而且我們隻能恰好走上 \(E\) 點，而不能在上面繞自環。

這就等價于我們走 \((N+1)/2-1=(N-1)/2\) 步，走到一個 \(A\) 類點。

是以我們就把那個矩陣的 \((N-1)/2\) 次幂算出來，枚舉 \(a\)，計算得 \(b=m-2a\)，求 \(B_b\) 到 \(A_a\) 的路徑數量的和，就是不合法的方案數。

不要忘記乘個 \(P\)。

每個的容斥背後，都有一個默默支援它的反演

常見的容斥，容斥系數是正負/正負+組合數的，本質是二項式反演

容斥系數帶 \(\mu\) 的，本質是莫比烏斯反演，本質的本質是在質因數的集合上二項式反演，\(\mu\) 是其容斥系數。

二項式反演，可以搞出來一堆集合的交/并，或者把“恰好”轉換成“至少”

如，CTS2019 随機立方體

容斥也可以結合dp，通過dp記錄容斥的貢獻來做

如，CTS2019 氪金手遊

由于這兩題都屬于機率期望，是以這裡不講（霧）

其實機率期望的本質也是數數 隻不過我懶得再寫一遍了qaq 去翻 “機率期望” 那篇罷

注，莫比烏斯容斥和這個東西的關系不大，是以這裡略

考慮直接瞎jr射，方案數是 \(n^n\) ，但肯定會有不射滿的 （戴黃看黃）

然後我們考慮容斥，容易想象到，我們應該這樣做：

射在 \(n\) 個數内 - 射在 \(n-1\) 個數内 + 射在 \(n-2\) 個數内...

這樣的容斥顯然是對的。想象一下正負号，得到：答案為

\[\sum\limits_{i=1}^{n} i^n\times (-1)^{n-i}\times \binom{n}{i}\]

可以用這個題來熱熱身。

如果您對容斥比較熟悉，不用動筆，用嘴巴就可以搞出這個題了。

反之，如果您用嘴巴切了這個題，說明您的容斥很強！

同樣涉及到一個映射的問題，考慮和上個題類似的做法：我們先不保證射滿，然後容斥。

先枚舉一個集合 \(S\)，并限制我們必須射在這裡面。然後做樹形dp：\(f(u,x)\) 表示，\(u\) 射到 \(x\)，\(u\) 子樹射的方案數。

枚舉 \(v\) 射到了 \(x'\)，那在原圖上 \(x\) 和 \(x'\) 之間就要有邊。如果有，就把這個方案加到 \(f(u,x)\) 裡面。

最後 \(f(1,*)\) 的和就是 \(S\) 的答案，容斥一下加起來即可。

（noi.ac的題有權限，這裡給出題意）

稱一個排列的子串為順子，當且僅當：這個子串裡兩兩之間差的絕對值為 \(\pm 1\) （即，連續單增/單減）

求 \(n\) 個數的排列中，有多少種排列滿足它所有順子的長度都 \(\le m\)。模 \(1e9+7\)。

\(m\le n\le 5000\)。

考慮反面，我們枚舉它有多少個長度為 \(m+1\) 的順子（枚舉左端點），其餘位置任意選，設這個方案為 \(c(i)\)。那麼答案為

\(c(0)-c(1)+c(2)-c(3)...=\sum\limits_{i}(-1)^i c(i)\)

然後我們發現，兩個順子如果有交，那它們必須同時遞增/遞減，然後我們就可以把它合并成一個大塊的順子，稱為一 “塊”

對于一個塊，它裡面選多少個長度為 \(m+1\) 的順子，我們其實并不知道。但是我們隻關心它們的方案數乘上容斥系數的和（因為這玩意就是答案）

對于塊之外的東西，每個位置都是獨立的數，稱為 “單點”

假設我們有 \(a\) 個塊，\(b\) 個單點，可以先安排出它們的相對順序，\((a+b)!\) 種方案，然後就可以唯一确定它們裡面填什麼數了。

對于一個塊，它可以增或者減，那就還有 \(2^a\) 種配置設定方法。

是以它們僅填數字的方案（即，不考慮結構和容斥系數）就是 \(2^a (a+b)!\) 種。

設 \(f(i,a,b)\) 表示前面 \(i\) 個數，選了 \(a\) 個塊，\(b\) 個單點，容斥貢獻和。

如果第 \(i\) 個位置是單點，那麼 \(f(i-1,a,b-1)\) 貢獻到 \(f(i,a,b)\)

如果第 \(i\) 個位置屬于一個塊，那就枚舉一個 \(j\) 表示上一塊的結尾，\(f(j,...)\) 貢獻過來。

發現這樣并不對，因為我們不能直接用 \(f\) 貢獻，因為 \(f\) 可能會有單點出來。

那我們再搞一個 \(g(i,a,b)\) ，表示強制令 \(i\) 為一個塊的結尾，的方案數。

那 \(f(i,a,b)=g(i,a,b)+f(i-1,a,b-1)\)

考慮 \(g\) 的轉移：

如果目前選的順子不和以前的重疊，貢獻和是 \(g(i-m-1,a-1,b)\)。由于多選了一個，容斥貢獻就乘一個 \(-1\)。

反之，就和以往的某個順子重疊了。那以前的順子，它的右端點要在 \([i-m,i-1]\) 裡面，并且選了這個順子之後，容斥系數乘 \(-1\)，而塊數不變，因為重疊了

可得：\(g(i,a,b)=-f(i-m-1,a-1,b)-g(i-m...i-1,a,b)\)。後面的 \(...\) 表示求和（這樣寫直覺些）

然後我們可以用字首和優化掉這個東西，複雜度 \(O(n^3)\)。

你開開心心的準備去寫，一看資料五千。

然後你發現這個轉移其實和 \(a+b\) 的關系比較大，注意到每次 \(a+b\) 這個東西隻會變化一個 \(-1\) 或者不變。

但我們也不能隻記一個 \(a+b\)，因為 \(a\) 還要貢獻一個 \(2^a\)

那我們為什麼不把這個 \(2^a\) 的貢獻也搞進來呢？那就隻需要記 \(a+b\) 了。

我們記 \(F(i,s)=\sum\limits_{a+b=s} 2^a\times f(i,a,b)\)，\(G(i,s)\) 同理。

我們把 \(F,G\) 的sigma裡面的 \(f,g\) 用上面的轉移化開，整理，把它們也搞成 \(F,G\) 的形式。得到：

\(F(i,s)=G(i,s)+F(i-1,s-1)\)

\(G(i,s)=-2F(i-m-1,s-1)-G(i-m...i-1,s)\)

為啥有一個 \(2\)？注意到那個 \(a-1\) 變成 \(a\) 的過程中，\(2^a\) 這個東西要變化的。

然後注意到空間開不下，考慮滾動數組。

接下來是一個 典 中 典： 如何滾 \(i\)？

注意到 \(i\) 這一維不太好滾。

是以我們滾 \(s\)。

​​這裡​​ 是完整的事件（

很多東西具有一個組合意義

比如上面提到 \(f(i)=2f(i-1)-f(i-m-1)\) 的那個遞推，它就可以看成DAG上的路徑計數。

同時，\(n^m\) 這個東西，也具有很好的意義：\(n\) 個數，選 \(m\) 次，選一個數之後不删除，方案數就是 \(n^m\)。

對于第 \(i\) 種序列， \(a_i^2\) 相當于：取兩次珠子，方案相同，且均為第 \(i\) 種序列的方案。

那麼我們取兩次珠子，方案相同，方案數就是 \(\sum a_i^2\)

接下來就好做了，注意到資料範圍非常小，設 \(f(a,b,a',b')\) 表示：第一次取 \(A\) 的 \(a\) 個，\(B\) 的 \(b\) 個第二次取 \(A\) 的 \(a'\) 個，\(B\) 的 \(b'\) 個，相同，的方案數。

注意到 \(a+b=a'+b'\)，故省去 \(b'\)，然後滾一下就行了。

和上一題類似。一段長度的平方，就相當于在這一段裡面選兩個位置的方案數。

而把這些平方乘起來，就相當于是在前 \(i\) 個裡面選 \(2k\) 個格子的方案數，根據乘法原理。

先不考慮障礙。設 \(f(i,0/1/2)\) 表示在前 \(i\) 個位置裡面分段之後選，最後一段裡面選了 \(0/1/2\) 個，的方案數。

第一種是，在 \(i-1,i\) 這裡劃開一段，然後 \(i\) 這個位置把目前的 \(j\) 個格子全部選掉。這種方案是 \(f(i-1,2)\)，前提是這一個位置不是障礙。

第二種是，\(i\) 和 \(i-1\) 在一段，考慮前面選了幾個，然後 \(i\) 這個位置上選剩下的（可能為 \(0\)）。枚舉一個 \(k\le j\)，這樣的方案數是 \(\binom{j}{k}\times f(i-1,k)\)。

于是，\(f(i,j)=f(i-1,2)+\sum\limits_{k=0}^{j} f(i-1,k)\times \binom{j}{k}\)

對于沒被障礙隔開的一段，用矩陣優化轉移。障礙特判一下就行。

複雜度 \(O(m\times 2^3\times \log n)\)。

這兩題的共同點是，需要求：長度為 \(n\) 的序列，每個數在 \([1,m]\) 間。設 \(L\) 表示最長連續相同段，求 \(L\) 的分布（即，對于每個 \(i\)，求 \(L=i\) 的方案數）

注意到，恰好不太好做，但是“不超過”感覺挺能做。

那我們現在要求最長連續相同段不超過 \(x\) 的方案，設為 \(g(i)\)。

考慮 \(i\) 所在的那一段多長，有轉移：\(g(i)=(m-1)\times (i-m...i-1)\)。

注意一個細節：我們認為每一段都隻能取 \(m-1\) 種，實際上第一段是可以取 \(m\) 種的。 最後乘一個 \(\dfrac{m}{m-1}\) 才是真正的答案。

字首和優化，設 \(s\) 為 \(g\) 的字首和。然後 \(s(i)-s(i-1)=(m-1)\times [s(i-1)-s(i-m-1)]\)。

移項，得 \(s(i)=m\times s(i-1)+(1-m)\times s(i-m-1)\)

然後和上面的一個轉化類似：把它看成DAG上的路徑計數。

枚舉跳了多少次 \(m+1\)，複雜度 \(O(\dfrac{n}{m})\)。枚舉 \(m\)，這樣算，複雜度是調和的。

然後就得到了 \(s\)。取差分得到 \(g\)。然後發現 \(g\) 的差分就是 \(L\) 分布了。

複雜度 \(O(n\ln n)\)。

有這樣一個式子，合法方案書=瞎選方案數*正确率。

假設我們能知道正确率，那問題就簡單了。

注意到 \((A,B)\) 的方案可以和 \(A,B\) 拼起來的方案一一對應。

現在問題變成一個序列：知道它有 \(a\) 個 \(1\) ，\(b\) 個 \(-m\)（和為 \(s=a-mb\)，保證是正的），每個位置的字首和都是正的，求方案數。設 \(n=a+b\) 為序列長度。

考慮一個序列的所有循環同構，我們發現，它一共有 \(n\) 個循環同構，而其中的恰好 \(s\) 個滿足字首和都是正的。

假設這個結論對，那就太好做了，答案是 \(\binom{a+b}{a}\times \dfrac{s}{n}\)。這就是 “瞎選方案數”乘以“正确率”。

證明如下

對于一個序列，我們把它寫無限遍。 設 \(las(x)\) 表示，字首和最後一次為 \(x\) 的位置。由于序列和為正，每過一個周期和就會增，是以這個 \(las\) 的值是有限的。 對于 \(i\in [1,s]\)，考慮 \([las(i)+1,las(i)+n]\) 這一段區間。根據 \(las\) 的定義，\(las\) 後面所有字首和都 \(>i\)。 那這麼說，這一段區間的字首和都嚴格的大于 \(i\)。 考慮區間内部的字首和，設 \(p\in [las(i)+1,las(i)+n]\)，則内部字首和就是 \((las(i),p]\) 的區間和，即 \(s_p-i\)。我們知道 \(s_p>i\)，是以這個和大于 \(0\)。 那我們把這一段區間取出來，它的每個位置字首和都 \(>0\)，是這個序列的一個循環同構。 是以我們有至少 \(s\) 個循環同構，使得它們任意位置字首和 \(>0\) 也容易發現，對于 \(i>s\)，它取出來的這段序列和 \(i-s\) 是本質相同的，是以不能算。 是以我們隻有 恰好 \(s\) 個循環同構是滿足條件的。