一、什麼是并查集?
并查集是一種用來管理元素分類的情況的資料結構,并查集可以高效的進行如下操作:
查詢元素a和b是否屬于同一組
合并元素a和元素b所在的組
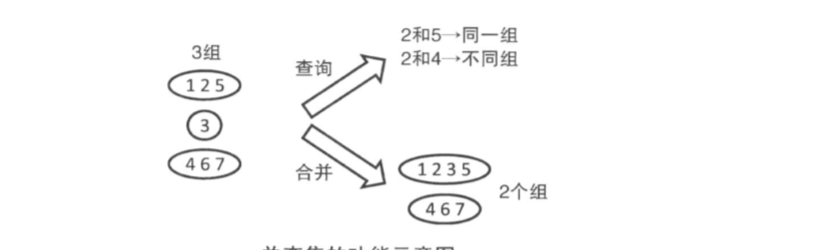
但不友善進行分割操作
二、并查集的結構
并查集也是使用樹形結構實作的,不過,不是二叉樹
每個元素對應一個節點,每個組對應一棵樹。在并查集中哪個節點是哪個節點的父親以及樹的形狀等資訊無需多加關注,整體形成一顆樹形結構才是重要的。
(1)初始化
我們準備n個節點來表示n個元素,最開始沒有邊(為了判斷根節點,每個節點添加一條指向相同節點的邊)
(2)查詢
為了查詢兩個節點是否屬于同一組,我們隻需判斷兩者的根節點是否相同。
(3)合并
從一個組的根向另一個組的根連邊,這樣兩棵樹就變成了一棵樹,也就把兩個組合成了一個組了。
三、并查集實作中的注意點
在樹形結構裡,一旦退化成鍊式結構,那麼複雜度就會變得很高。是以有必要想辦法避免退化的發生。
(1)對于每棵樹記錄這棵樹的高度(rank)
合并時如果兩棵樹的rank不同,那麼從rank小的向rank大的連邊。
(2)此外,也可以通過路徑壓縮
對于每個節點,一旦向上走到了一次根節點,就把這個點到父親的邊改為直接指向根。
在此之上,不僅僅是所查詢的節點,在查詢過程中向上經過的的所有節點,如果不是直接連到根上,都改為直接連到根上。
這樣再次查詢這些節點時,就可以很快知道根時誰了。
在使用這種方法時,為了簡單起見,即使樹的高度發生了變化,我們也不修改rank的值,即方法一與方法二使用其中一個就可以了
方法二簡化的效率高,而且便于編寫,推薦使用方法二。
四、并查集的複雜度(平均複雜度)
加入這兩個優化後的并查集效率非常高。對n個元素的并查集進行一次操作的額複雜度是O(α(n)),α(n)是阿克曼(Ackermann)函數的反函數。這比O(log(n))還要快。
五、并查集的代碼實作
我們用編号代表每個元素,數組par表示父節點的編号,fa[x] = x是,說明x是所在樹的根節點。
1 const int maxn = 100000 + 10;
2 int fa[maxn]; //fa父節點
3
4 //初始化n個節點
5 void init(int n)
6 {
7 for (int i = 0; i <= n; i++)
8 fa[i] = i;
9 }
10
11 //查詢樹的根
12 int find(int x)
13 {
14 if (x != fa[x])
15 return fa[x] = find(fa[x]);
16 return fa[x];
17 }
18
19 //合并x和y所屬的集合
20 void unite(int x, int y)
21 {
22 int rx = find(x);
23 int ry = find(y);
24 if (rx == ry) return;
25
26 fa[rx] = ry;
27 }
28
29 //判斷x和y是否屬于同一集合
30 bool same(int x, int y)
31 {
32 return find(x) == find(y);
33 } 個性簽名:時間會解決一切